ABACABA pattern
The ABACABA pattern is a recursive fractal pattern that shows up in many places in the real world (such as in geometry, art, music, poetry, number systems, literature and higher dimensions).[1][2][3][4] Patterns often show a DABACABA type subset. AA, ABBA, and ABAABA type forms are also considered.[5]
Generating the pattern
In order to generate the next sequence, first take the previous pattern, add the next letter from the alphabet, and then repeat the previous pattern. The first few steps are listed here.[4] A generator can be found here
| Step | Pattern | Letters |
|---|---|---|
| 1 | A | 21 − 1 = 1 |
| 2 | ABA | 3 |
| 3 | ABACABA | 7 |
| 4 | ABACABADABACABA | 15 |
| 5 | ABACABADABACABAEABACABADABACABA | 31 |
| 6 | ABACABADABACABAEABACABADABACABAFABACABADABACABAEABACABADABACABA | 63 |
ABACABA is a "quickly growing word", often described as chiastic or "symmetrically organized around a central axis" (see: Chiastic structure and Χ).[4] The number of members in each iteration is a(n) = 2n − 1, the Mersenne numbers (OEIS: A000225).
Gallery
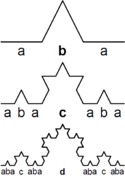
Koch curve:[1] [math]\displaystyle{ n=1 }[/math] is ABA, [math]\displaystyle{ n=2 }[/math] is ABACABA, and [math]\displaystyle{ n=3 }[/math]: ABACABADABACABA
- Metric hierarchy:
ABACABADABACABA[lower-alpha 1] - Metric levels:[1]EABACABADABACABA
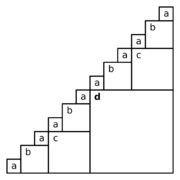
- A staircase built with the largest possible squares/cubes while allowing equally sized steps:ABACABADABACABA[1]
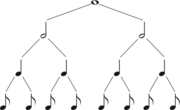
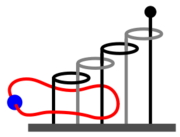
- The Tower of Hanoi[1] with four disks:ABACABADABACABA
- Binary-reflected Gray code (BRGC):to G
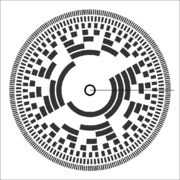
- Rotary encoder:to I
- 3-bit Gray code visualized as a traversal of vertices of a cube (0,1,3,2,6,7,5,4):[1]ABACABA
- Château de Chambord:ABACABA[6]
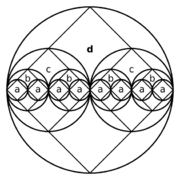
- Devil's needle:[1]ABACABADABACABA
See also
Notes
- ↑ The strength, emphasis, or importance of the beginning of each duration [math]\displaystyle{ 1/8 }[/math] the length of a single measure in 44 (eighth-notes) is, divisively ([math]\displaystyle{ 2/2^1=1 }[/math], [math]\displaystyle{ 4/2^2=1 }[/math], [math]\displaystyle{ 8/2^3=1 }[/math]), determined by each eighth-note's position in a DABACABA structure, while the eighth notes of two measures grouped, additively ([math]\displaystyle{ 8\times2=16 }[/math]), are determined by an EABACABADABACABA structure.[3]
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 Naylor, Mike (February 2013). "ABACABA Amazing Pattern, Amazing Connections" (in en). Math Horizons. http://digitaleditions.walsworthprintgroup.com/display_article.php?id=1300604.
- ↑ 2.0 2.1 2.2 2.3 SheriOZ (2016-04-21). "Exploring Fractals with ABACABA" (in en-US). Chicago Geek Guy. http://chicagogeekguy.com/exploring-abacaba/.
- ↑ 3.0 3.1 Naylor, Mike (2011). "Abacaba! – Using a mathematical pattern to connect art, music, poetry and literature". http://archive.bridgesmathart.org/2011/bridges2011-89.pdf.
- ↑ 4.0 4.1 4.2 Conley, Craig (2008-10-01) (in en). Magic Words: A Dictionary. Weiser Books. p. 53. ISBN 9781609250508. https://books.google.com/books?id=3SB60Wavy6MC&q=Abacaba+pattern+-wikipedia.org&pg=PA53.
- ↑ Halter-Koch, Franz and Tichy, Robert F.; eds. (2000). Algebraic Number Theory and Diophantine Analysis, p.478. W. de Gruyter. ISBN:9783110163049.
- ↑ Wright, Craig (2016). Listening to Western Music, p.48. Cengage Learning. ISBN:9781305887039.
External links
- Naylor, Mike: abacaba.org
 |