Fractal

In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set.[1][2][3][4] This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar.[5] Fractal geometry lies within the mathematical branch of measure theory.
One way that fractals are different from finite geometric figures is how they scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). Likewise, if the radius of a filled sphere is doubled, its volume scales by eight, which is two (the ratio of the new to the old radius) to the power of three (the conventional dimension of the filled sphere). However, if a fractal's one-dimensional lengths are all doubled, the spatial content of the fractal scales by a power that is not necessarily an integer and is in general greater than its conventional dimension.[1] This power is called the fractal dimension of the geometric object, to distinguish it from the conventional dimension (which is formally called the topological dimension).[6]
Analytically, many fractals are nowhere differentiable.[1][4] An infinite fractal curve can be conceived of as winding through space differently from an ordinary line – although it is still topologically 1-dimensional, its fractal dimension indicates that it locally fills space more efficiently than an ordinary line.[1][6]

Starting in the 17th century with notions of recursion, fractals have moved through increasingly rigorous mathematical treatment to the study of continuous but not differentiable functions in the 19th century by the seminal work of Bernard Bolzano, Bernhard Riemann, and Karl Weierstrass,[7] and on to the coining of the word fractal in the 20th century with a subsequent burgeoning of interest in fractals and computer-based modelling in the 20th century.[8][9]
There is some disagreement among mathematicians about how the concept of a fractal should be formally defined. Mandelbrot himself summarized it as "beautiful, damn hard, increasingly useful. That's fractals."[10] More formally, in 1982 Mandelbrot defined fractal as follows: "A fractal is by definition a set for which the Hausdorff–Besicovitch dimension strictly exceeds the topological dimension."[11] Later, seeing this as too restrictive, he simplified and expanded the definition to this: "A fractal is a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole."[1] Still later, Mandelbrot proposed "to use fractal without a pedantic definition, to use fractal dimension as a generic term applicable to all the variants".[12]
The consensus among mathematicians is that theoretical fractals are infinitely self-similar iterated and detailed mathematical constructs, of which many examples have been formulated and studied.[1][2][3] Fractals are not limited to geometric patterns, but can also describe processes in time.[5][4][13][14][15][16] Fractal patterns with various degrees of self-similarity have been rendered or studied in visual, physical, and aural media[17] and found in nature,[18][19][20][21] technology,[22][23][24][25] art,[26][27] and architecture.[28] Fractals are of particular relevance in the field of chaos theory because they show up in the geometric depictions of most chaotic processes (typically either as attractors or as boundaries between basins of attraction).[29]
Etymology
The term "fractal" was coined by the mathematician Benoît Mandelbrot in 1975.[30] Mandelbrot based it on the Latin frāctus, meaning "broken" or "fractured", and used it to extend the concept of theoretical fractional dimensions to geometric patterns in nature.[1][31][32]
Introduction
The word "fractal" often has different connotations for the lay public as opposed to mathematicians, where the public is more likely to be familiar with fractal art than the mathematical concept. The mathematical concept is difficult to define formally, even for mathematicians, but key features can be understood with a little mathematical background.
The feature of "self-similarity", for instance, is easily understood by analogy to zooming in with a lens or other device that zooms in on digital images to uncover finer, previously invisible, new structure. If this is done on fractals, however, no new detail appears; nothing changes and the same pattern repeats over and over, or for some fractals, nearly the same pattern reappears over and over. Self-similarity itself is not necessarily counter-intuitive (e.g., people have pondered self-similarity informally such as in the infinite regress in parallel mirrors or the homunculus, the little man inside the head of the little man inside the head ...). The difference for fractals is that the pattern reproduced must be detailed.[1]:166; 18[2][31]
This idea of being detailed relates to another feature that can be understood without much mathematical background: Having a fractal dimension greater than its topological dimension, for instance, refers to how a fractal scales compared to how geometric shapes are usually perceived. A straight line, for instance, is conventionally understood to be one-dimensional; if such a figure is rep-tiled into pieces each 1/3 the length of the original, then there are always three equal pieces. A solid square is understood to be two-dimensional; if such a figure is rep-tiled into pieces each scaled down by a factor of 1/3 in both dimensions, there are a total of 32 = 9 pieces.
We see that for ordinary self-similar objects, being n-dimensional means that when it is rep-tiled into pieces each scaled down by a scale-factor of 1/r, there are a total of rn pieces. Now, consider the Koch curve. It can be rep-tiled into four sub-copies, each scaled down by a scale-factor of 1/3. So, strictly by analogy, we can consider the "dimension" of the Koch curve as being the unique real number D that satisfies 3D = 4. This number is called the fractal dimension of the Koch curve; it is not the conventionally perceived dimension of a curve. In general, a key property of fractals is that the fractal dimension differs from the conventionally understood dimension (formally called the topological dimension).
This also leads to understanding a third feature, that fractals as mathematical equations are "nowhere differentiable". In a concrete sense, this means fractals cannot be measured in traditional ways.[1][4][33] To elaborate, in trying to find the length of a wavy non-fractal curve, one could find straight segments of some measuring tool small enough to lay end to end over the waves, where the pieces could get small enough to be considered to conform to the curve in the normal manner of measuring with a tape measure. But in measuring an infinitely "wiggly" fractal curve such as the Koch snowflake, one would never find a small enough straight segment to conform to the curve, because the jagged pattern would always re-appear, at arbitrarily small scales, essentially pulling a little more of the tape measure into the total length measured each time one attempted to fit it tighter and tighter to the curve. The result is that one must need infinite tape to perfectly cover the entire curve, i.e. the snowflake has an infinite perimeter.[1]
History
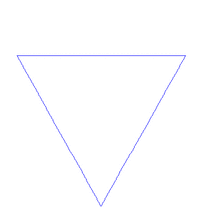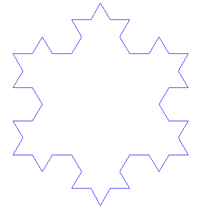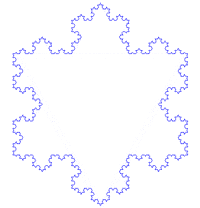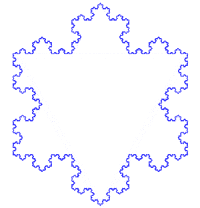
The history of fractals traces a path from chiefly theoretical studies to modern applications in computer graphics, with several notable people contributing canonical fractal forms along the way.[8][9] A common theme in traditional African architecture is the use of fractal scaling, whereby small parts of the structure tend to look similar to larger parts, such as a circular village made of circular houses.[34] According to Pickover, the mathematics behind fractals began to take shape in the 17th century when the mathematician and philosopher Gottfried Leibniz pondered recursive self-similarity (although he made the mistake of thinking that only the straight line was self-similar in this sense).[35]
In his writings, Leibniz used the term "fractional exponents", but lamented that "Geometry" did not yet know of them.[1]:405 Indeed, according to various historical accounts, after that point few mathematicians tackled the issues and the work of those who did remained obscured largely because of resistance to such unfamiliar emerging concepts, which were sometimes referred to as mathematical "monsters".[33][8][9] Thus, it was not until two centuries had passed that on July 18, 1872 Karl Weierstrass presented the first definition of a function with a graph that would today be considered a fractal, having the non-intuitive property of being everywhere continuous but nowhere differentiable at the Royal Prussian Academy of Sciences.[8]:7[9]
In addition, the quotient difference becomes arbitrarily large as the summation index increases.[36] Not long after that, in 1883, Georg Cantor, who attended lectures by Weierstrass,[9] published examples of subsets of the real line known as Cantor sets, which had unusual properties and are now recognized as fractals.[8]:11–24 Also in the last part of that century, Felix Klein and Henri Poincaré introduced a category of fractal that has come to be called "self-inverse" fractals.[1]:166

One of the next milestones came in 1904, when Helge von Koch, extending ideas of Poincaré and dissatisfied with Weierstrass's abstract and analytic definition, gave a more geometric definition including hand-drawn images of a similar function, which is now called the Koch snowflake.[8]:25[9] Another milestone came a decade later in 1915, when Wacław Sierpiński constructed his famous triangle then, one year later, his carpet. By 1918, two French mathematicians, Pierre Fatou and Gaston Julia, though working independently, arrived essentially simultaneously at results describing what is now seen as fractal behaviour associated with mapping complex numbers and iterative functions and leading to further ideas about attractors and repellors (i.e., points that attract or repel other points), which have become very important in the study of fractals.[4][8][9]
Very shortly after that work was submitted, by March 1918, Felix Hausdorff expanded the definition of "dimension", significantly for the evolution of the definition of fractals, to allow for sets to have non-integer dimensions.[9] The idea of self-similar curves was taken further by Paul Lévy, who, in his 1938 paper Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole, described a new fractal curve, the Lévy C curve.[notes 1]
Different researchers have postulated that without the aid of modern computer graphics, early investigators were limited to what they could depict in manual drawings, so lacked the means to visualize the beauty and appreciate some of the implications of many of the patterns they had discovered (the Julia set, for instance, could only be visualized through a few iterations as very simple drawings).[1]:179[33][9] That changed, however, in the 1960s, when Benoit Mandelbrot started writing about self-similarity in papers such as How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension,[37][38] which built on earlier work by Lewis Fry Richardson.
In 1975,[31] Mandelbrot solidified hundreds of years of thought and mathematical development in coining the word "fractal" and illustrated his mathematical definition with striking computer-constructed visualizations. These images, such as of his canonical Mandelbrot set, captured the popular imagination; many of them were based on recursion, leading to the popular meaning of the term "fractal".[39][33][8][35]
In 1980, Loren Carpenter gave a presentation at the SIGGRAPH where he introduced his software for generating and rendering fractally generated landscapes.[40]
Definition and characteristics
One often cited description that Mandelbrot published to describe geometric fractals is "a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole";[1] this is generally helpful but limited. Authors disagree on the exact definition of fractal, but most usually elaborate on the basic ideas of self-similarity and the unusual relationship fractals have with the space they are embedded in.[1][5][2][4][41]
One point agreed on is that fractal patterns are characterized by fractal dimensions, but whereas these numbers quantify complexity (i.e., changing detail with changing scale), they neither uniquely describe nor specify details of how to construct particular fractal patterns.[42] In 1975 when Mandelbrot coined the word "fractal", he did so to denote an object whose Hausdorff–Besicovitch dimension is greater than its topological dimension.[31] However, this requirement is not met by space-filling curves such as the Hilbert curve.[notes 2]
Because of the trouble involved in finding one definition for fractals, some argue that fractals should not be strictly defined at all. According to Falconer, fractals should be only generally characterized by a gestalt of the following features;[2]
- Self-similarity, which may include:
- Exact self-similarity: identical at all scales, such as the Koch snowflake
- Quasi self-similarity: approximates the same pattern at different scales; may contain small copies of the entire fractal in distorted and degenerate forms; e.g., the Mandelbrot set's satellites are approximations of the entire set, but not exact copies.
- Statistical self-similarity: repeats a pattern stochastically so numerical or statistical measures are preserved across scales; e.g., randomly generated fractals like the well-known example of the coastline of Britain for which one would not expect to find a segment scaled and repeated as neatly as the repeated unit that defines fractals like the Koch snowflake.[4]
- Qualitative self-similarity: as in a time series[13]
- Multifractal scaling: characterized by more than one fractal dimension or scaling rule
- Fine or detailed structure at arbitrarily small scales. A consequence of this structure is fractals may have emergent properties[43] (related to the next criterion in this list).
- Irregularity locally and globally that cannot easily be described in the language of traditional Euclidean geometry other than as the limit of a recursively defined sequence of stages. For images of fractal patterns, this has been expressed by phrases such as "smoothly piling up surfaces" and "swirls upon swirls";[6]see Common techniques for generating fractals.
As a group, these criteria form guidelines for excluding certain cases, such as those that may be self-similar without having other typically fractal features. A straight line, for instance, is self-similar but not fractal because it lacks detail, and is easily described in Euclidean language without a need for recursion.[1][4]
Common techniques for generating fractals

Images of fractals can be created by fractal generating programs. Because of the butterfly effect, a small change in a single variable can have an unpredictable outcome.
- Iterated function systems (IFS) – use fixed geometric replacement rules; may be stochastic or deterministic;[44] e.g., Koch snowflake, Cantor set, Haferman carpet,[45] Sierpinski carpet, Sierpinski gasket, Peano curve, Harter-Heighway dragon curve, T-square, Menger sponge
- Strange attractors – use iterations of a map or solutions of a system of initial-value differential or difference equations that exhibit chaos (e.g., see multifractal image, or the logistic map)
- L-systems – use string rewriting; may resemble branching patterns, such as in plants, biological cells (e.g., neurons and immune system cells[21]), blood vessels, pulmonary structure,[46] etc. or turtle graphics patterns such as space-filling curves and tilings
- Escape-time fractals – use a formula or recurrence relation at each point in a space (such as the complex plane); usually quasi-self-similar; also known as "orbit" fractals; e.g., the Mandelbrot set, Julia set, Burning Ship fractal, Nova fractal and Lyapunov fractal. The 2d vector fields that are generated by one or two iterations of escape-time formulae also give rise to a fractal form when points (or pixel data) are passed through this field repeatedly.
- Random fractals – use stochastic rules; e.g., Lévy flight, percolation clusters, self avoiding walks, fractal landscapes, trajectories of Brownian motion and the Brownian tree (i.e., dendritic fractals generated by modeling diffusion-limited aggregation or reaction-limited aggregation clusters).[4]

- Finite subdivision rules – use a recursive topological algorithm for refining tilings[47] and they are similar to the process of cell division.[48] The iterative processes used in creating the Cantor set and the Sierpinski carpet are examples of finite subdivision rules, as is barycentric subdivision.
Applications
Simulated fractals
Fractal patterns have been modeled extensively, albeit within a range of scales rather than infinitely, owing to the practical limits of physical time and space. Models may simulate theoretical fractals or natural phenomena with fractal features. The outputs of the modelling process may be highly artistic renderings, outputs for investigation, or benchmarks for fractal analysis. Some specific applications of fractals to technology are listed elsewhere. Images and other outputs of modelling are normally referred to as being "fractals" even if they do not have strictly fractal characteristics, such as when it is possible to zoom into a region of the fractal image that does not exhibit any fractal properties. Also, these may include calculation or display artifacts which are not characteristics of true fractals.
Modeled fractals may be sounds,[17] digital images, electrochemical patterns, circadian rhythms,[49] etc. Fractal patterns have been reconstructed in physical 3-dimensional space[24]:10 and virtually, often called "in silico" modeling.[46] Models of fractals are generally created using fractal-generating software that implements techniques such as those outlined above.[4][13][24] As one illustration, trees, ferns, cells of the nervous system,[21] blood and lung vasculature,[46] and other branching patterns in nature can be modeled on a computer by using recursive algorithms and L-systems techniques.[21]
The recursive nature of some patterns is obvious in certain examples—a branch from a tree or a frond from a fern is a miniature replica of the whole: not identical, but similar in nature. Similarly, random fractals have been used to describe/create many highly irregular real-world objects, such as coastlines and mountains. A limitation of modeling fractals is that resemblance of a fractal model to a natural phenomenon does not prove that the phenomenon being modeled is formed by a process similar to the modeling algorithms.
Natural phenomena with fractal features
Approximate fractals found in nature display self-similarity over extended, but finite, scale ranges. The connection between fractals and leaves, for instance, is currently being used to determine how much carbon is contained in trees.[50] Phenomena known to have fractal features include:
- Actin cytoskeleton[51]
- Algae
- Animal coloration patterns
- Blood vessels and pulmonary vessels[46]
- Brownian motion (generated by a one-dimensional Wiener process).[52]
- Clouds and rainfall areas[53]
- Coastlines
- Craters
- Crystals[54]
- DNA
- Dust grains[55]
- Earthquakes[25][56]
- Fault lines
- Geometrical optics[57]
- Heart rates[18]
- Heart sounds
- Lake shorelines and areas[58][59][60]
- Lightning bolts
- Mountain-goat horns
- Neurons
- Polymers
- Percolation
- Mountain ranges
- Ocean waves[61]
- Pineapple
- Proteins[62]
- Psychedelic Experience
- Purkinje cells[63]
- Rings of Saturn[64][65]
- River networks
- Romanesco broccoli
- Snowflakes[66]
- Soil pores[67]
- Surfaces in turbulent flows[68][69]
- Trees
Fractal basin boundary in a geometrical optical system[57]
A fractal is formed when pulling apart two glue-covered acrylic sheets
High-voltage breakdown within a 4 in (100 mm) block of acrylic glass creates a fractal Lichtenberg figure
Romanesco broccoli, showing self-similar form approximating a natural fractal
Slime mold Brefeldia maxima growing fractally on wood
Fractals in cell biology
Fractals often appear in the realm of living organisms where they arise through branching processes and other complex pattern formation. Ian Wong and co-workers have shown that migrating cells can form fractals by clustering and branching.[70] Nerve cells function through processes at the cell surface, with phenomena that are enhanced by largely increasing the surface to volume ratio. As a consequence nerve cells often are found to form into fractal patterns.[71] These processes are crucial in cell physiology and different pathologies.[72]
Multiple subcellular structures also are found to assemble into fractals. Diego Krapf has shown that through branching processes the actin filaments in human cells assemble into fractal patterns.[57] Similarly Matthias Weiss showed that the endoplasmic reticulum displays fractal features.[73] The current understanding is that fractals are ubiquitous in cell biology, from proteins, to organelles, to whole cells.
In creative works
Since 1999 numerous scientific groups have performed fractal analysis on over 50 paintings created by Jackson Pollock by pouring paint directly onto horizontal canvasses.[74][75] [76]
Recently, fractal analysis has been used to achieve a 93% success rate in distinguishing real from imitation Pollocks.[77] Cognitive neuroscientists have shown that Pollock's fractals induce the same stress-reduction in observers as computer-generated fractals and Nature's fractals.[78]
Decalcomania, a technique used by artists such as Max Ernst, can produce fractal-like patterns.[79] It involves pressing paint between two surfaces and pulling them apart.
Cyberneticist Ron Eglash has suggested that fractal geometry and mathematics are prevalent in African art, games, divination, trade, and architecture. Circular houses appear in circles of circles, rectangular houses in rectangles of rectangles, and so on. Such scaling patterns can also be found in African textiles, sculpture, and even cornrow hairstyles.[27][80] Hokky Situngkir also suggested the similar properties in Indonesian traditional art, batik, and ornaments found in traditional houses.[81][82]
Ethnomathematician Ron Eglash has discussed the planned layout of Benin city using fractals as the basis, not only in the city itself and the villages but even in the rooms of houses. He commented that "When Europeans first came to Africa, they considered the architecture very disorganised and thus primitive. It never occurred to them that the Africans might have been using a form of mathematics that they hadn't even discovered yet."[83]
In a 1996 interview with Michael Silverblatt, David Foster Wallace explained that the structure of the first draft of Infinite Jest he gave to his editor Michael Pietsch was inspired by fractals, specifically the Sierpinski triangle (a.k.a. Sierpinski gasket), but that the edited novel is "more like a lopsided Sierpinsky Gasket".[26]
Some works by the Dutch artist M. C. Escher, such as Circle Limit III, contain shapes repeated to infinity that become smaller and smaller as they get near to the edges, in a pattern that would always look the same if zoomed in.
Aesthetics and Psychological Effects of Fractal Based Design:[84] Highly prevalent in nature, fractal patterns possess self-similar components that repeat at varying size scales. The perceptual experience of human-made environments can be impacted with inclusion of these natural patterns. Previous work has demonstrated consistent trends in preference for and complexity estimates of fractal patterns. However, limited information has been gathered on the impact of other visual judgments. Here we examine the aesthetic and perceptual experience of fractal ‘global-forest’ designs already installed in humanmade spaces and demonstrate how fractal pattern components are associated with positive psychological experiences that can be utilized to promote occupant well-being. These designs are composite fractal patterns consisting of individual fractal ‘tree-seeds’ which combine to create a ‘global fractal forest.’ The local ‘tree-seed’ patterns, global configuration of tree-seed locations, and overall resulting ‘global-forest’ patterns have fractal qualities. These designs span multiple mediums yet are all intended to lower occupant stress without detracting from the function and overall design of the space. In this series of studies, we first establish divergent relationships between various visual attributes, with pattern complexity, preference, and engagement ratings increasing with fractal complexity compared to ratings of refreshment and relaxation which stay the same or decrease with complexity. Subsequently, we determine that the local constituent fractal (‘tree-seed’) patterns contribute to the perception of the overall fractal design, and address how to balance aesthetic and psychological effects (such as individual experiences of perceived engagement and relaxation) in fractal design installations. This set of studies demonstrates that fractal preference is driven by a balance between increased arousal (desire for engagement and complexity) and decreased tension (desire for relaxation or refreshment). Installations of these composite mid-high complexity ‘global-forest’ patterns consisting of ‘tree-seed’ components balance these contrasting needs, and can serve as a practical implementation of biophilic patterns in human-made environments to promote occupant well-being.
Physiological responses
Humans appear to be especially well-adapted to processing fractal patterns with D values between 1.3 and 1.5.[85] When humans view fractal patterns with D values between 1.3 and 1.5, this tends to reduce physiological stress.[86][87]
Applications in technology
- Fractal antennas[88]
- Fractal transistor[89]
- Fractal heat exchangers[90]
- Digital imaging
- Architecture[28]
- Urban growth[91][92]
- Classification of histopathology slides
- Fractal landscape or Coastline complexity
- Detecting 'life as we don't know it' by fractal analysis[93]
- Enzymes (Michaelis–Menten kinetics)
- Generation of new music
- Signal and image compression
- Creation of digital photographic enlargements
- Fractal in soil mechanics
- Computer and video game design
- Computer Graphics
- Organic environments
- Procedural generation
- Fractography and fracture mechanics
- Small angle scattering theory of fractally rough systems
- T-shirts and other fashion
- Generation of patterns for camouflage, such as MARPAT
- Digital sundial
- Technical analysis of price series
- Fractals in networks
- Medicine[24]
- Neuroscience[19][20]
- Diagnostic Imaging[23]
- Pathology[94][95]
- Geology[96]
- Geography[97]
- Archaeology[98][99]
- Soil mechanics[22]
- Seismology[25]
- Search and rescue[100]
- Morton order space filling curves for GPU cache coherency in texture mapping,[101][102][103] rasterisation[104][105] and indexing of turbulence data.[106][107]
See also
- Banach fixed point theorem
- Bifurcation theory – Study of sudden qualitative behavior changes caused by small parameter changes
- Box counting – Fractal analysis technique
- Cymatics – Creation of visible patterns on a vibrated plate
- Determinism – Philosophical view that events are pre-determined
- Diamond-square algorithm – Method for generating heightmaps for computer graphics
- Droste effect – Recursive visual effect
- Feigenbaum function
- Form constant
- Fractal cosmology
- Fractal derivative – Generalization of derivative to fractals
- Fractalgrid
- Fractal string
- Fracton – Synonym of phonon
- Graftal
- Greeble – Fine relief detailing added to a surface to make it appear more complex
- Infinite regress – Philosophical problem
- Lacunarity – Term in geometry and fractal analysis
- List of fractals by Hausdorff dimension
- Mandelbulb – Three-dimensional fractal
- Mandelbox – Fractal with a boxlike shape
- Macrocosm and microcosm
- Matryoshka doll – Russian nested wooden toy
- Menger Sponge
- Multifractal system – System with multiple fractal dimensions
- Newton fractal – Boundary set in the complex plane
- Percolation – Filtration of fluids through porous materials
- Power law – Functional relationship between two quantities
- Publications in fractal geometry – None
- Random walk – Mathematical formalization of a path that consists of a succession of random steps
- Self-reference – Sentence, idea or formula that refers to itself
- Self-similarity – Whole of an object being mathematically similar to part of itself
- Systems theory – Interdisciplinary study of systems
- Strange loop – Cyclic structure that goes through several levels in a hierarchical system
- Turbulence
- Wiener process – Stochastic process generalizing Brownian motion
Notes
- ↑ The original paper, Lévy, Paul (1938). "Les Courbes planes ou gauches et les surfaces composées de parties semblables au tout". Journal de l'École Polytechnique: 227–247, 249–291., is translated in Edgar, pages 181–239.
- ↑ The Hilbert curve map is not a homeomorphism, so it does not preserve topological dimension. The topological dimension and Hausdorff dimension of the image of the Hilbert map in R2 are both 2. Note, however, that the topological dimension of the graph of the Hilbert map (a set in R3) is 1.
References
- ↑ Jump up to: 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 Mandelbrot, Benoît B. (1983). The fractal geometry of nature. Macmillan. ISBN 978-0-7167-1186-5. https://books.google.com/books?id=0R2LkE3N7-oC.
- ↑ Jump up to: 2.0 2.1 2.2 2.3 2.4 Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons. pp. xxv. ISBN 978-0-470-84862-3.
- ↑ Jump up to: 3.0 3.1 Briggs, John (1992). Fractals:The Patterns of Chaos. London: Thames and Hudson. p. 148. ISBN 978-0-500-27693-8.
- ↑ Jump up to: 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 Vicsek, Tamás (1992). Fractal growth phenomena. Singapore/New Jersey: World Scientific. pp. 31; 139–146. ISBN 978-981-02-0668-0.
- ↑ Jump up to: 5.0 5.1 5.2 Gouyet, Jean-François (1996). Physics and fractal structures. Paris/New York: Masson Springer. ISBN 978-0-387-94153-0.
- ↑ Jump up to: 6.0 6.1 6.2 Mandelbrot, Benoît B. (2004). Fractals and Chaos. Berlin: Springer. p. 38. ISBN 978-0-387-20158-0. "A fractal set is one for which the fractal (Hausdorff-Besicovitch) dimension strictly exceeds the topological dimension"
- ↑ Segal, S. L. (June 1978). "Riemann's example of a continuous 'nondifferentiable' function continued". The Mathematical Intelligencer 1 (2): 81–82. doi:10.1007/BF03023065.
- ↑ Jump up to: 8.0 8.1 8.2 8.3 8.4 8.5 8.6 8.7 Edgar, Gerald (2004). Classics on Fractals. Boulder, CO: Westview Press. ISBN 978-0-8133-4153-8.
- ↑ Jump up to: 9.0 9.1 9.2 9.3 9.4 9.5 9.6 9.7 9.8 Trochet, Holly (2009). "A History of Fractal Geometry". MacTutor History of Mathematics. http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/fractals.html.
- ↑ Mandelbrot, Benoit. "24/7 Lecture on Fractals". 2006 Ig Nobel Awards. Improbable Research. https://www.youtube.com/watch?v=5e7HB5Oze4g#t=70.
- ↑ Mandelbrot, B. B.: The Fractal Geometry of Nature. W. H. Freeman and Company, New York (1982); p. 15.
- ↑ Edgar, Gerald (2007). Measure, Topology, and Fractal Geometry. Springer Science & Business Media. p. 7. ISBN 978-0-387-74749-1. https://books.google.com/books?id=dk2vruTv0_gC&pg=PR7.
- ↑ Jump up to: 13.0 13.1 13.2 Peters, Edgar (1996). Chaos and order in the capital markets : a new view of cycles, prices, and market volatility. New York: Wiley. ISBN 978-0-471-13938-6.
- ↑ Krapivsky, P. L.; Ben-Naim, E. (1994). "Multiscaling in Stochastic Fractals". Physics Letters A 196 (3–4): 168. doi:10.1016/0375-9601(94)91220-3. Bibcode: 1994PhLA..196..168K.
- ↑ Hassan, M. K.; Rodgers, G. J. (1995). "Models of fragmentation and stochastic fractals". Physics Letters A 208 (1–2): 95. doi:10.1016/0375-9601(95)00727-k. Bibcode: 1995PhLA..208...95H.
- ↑ Hassan, M. K.; Pavel, N. I.; Pandit, R. K.; Kurths, J. (2014). "Dyadic Cantor set and its kinetic and stochastic counterpart". Chaos, Solitons & Fractals 60: 31–39. doi:10.1016/j.chaos.2013.12.010. Bibcode: 2014CSF....60...31H.
- ↑ Jump up to: 17.0 17.1 Brothers, Harlan J. (2007). "Structural Scaling in Bach's Cello Suite No. 3". Fractals 15 (1): 89–95. doi:10.1142/S0218348X0700337X.
- ↑ Jump up to: 18.0 18.1 Tan, Can Ozan; Cohen, Michael A.; Eckberg, Dwain L.; Taylor, J. Andrew (2009). "Fractal properties of human heart period variability: Physiological and methodological implications". The Journal of Physiology 587 (15): 3929–41. doi:10.1113/jphysiol.2009.169219. PMID 19528254.
- ↑ Jump up to: 19.0 19.1 Liu, Jing Z.; Zhang, Lu D.; Yue, Guang H. (2003). "Fractal Dimension in Human Cerebellum Measured by Magnetic Resonance Imaging". Biophysical Journal 85 (6): 4041–4046. doi:10.1016/S0006-3495(03)74817-6. PMID 14645092. Bibcode: 2003BpJ....85.4041L.
- ↑ Jump up to: 20.0 20.1 Karperien, Audrey L.; Jelinek, Herbert F.; Buchan, Alastair M. (2008). "Box-Counting Analysis of Microglia Form in Schizophrenia, Alzheimer's Disease and Affective Disorder". Fractals 16 (2): 103. doi:10.1142/S0218348X08003880.
- ↑ Jump up to: 21.0 21.1 21.2 21.3 21.4 Jelinek, Herbert F.; Karperien, Audrey; Cornforth, David; Cesar, Roberto; Leandro, Jorge de Jesus Gomes (2002). "MicroMod-an L-systems approach to neural modelling". in Sarker, Ruhul. Workshop proceedings: the Sixth Australia-Japan Joint Workshop on Intelligent and Evolutionary Systems, University House, ANU. University of New South Wales. ISBN 978-0-7317-0505-4. OCLC 224846454. https://books.google.com/books?id=FFSUGQAACAAJ. Retrieved February 3, 2012. "Event location: Canberra, Australia"
- ↑ Jump up to: 22.0 22.1 Hu, Shougeng; Cheng, Qiuming; Wang, Le; Xie, Shuyun (2012). "Multifractal characterization of urban residential land price in space and time". Applied Geography 34: 161–170. doi:10.1016/j.apgeog.2011.10.016.
- ↑ Jump up to: 23.0 23.1 Karperien, Audrey; Jelinek, Herbert F.; Leandro, Jorge de Jesus Gomes; Soares, João V. B.; Cesar Jr, Roberto M.; Luckie, Alan (2008). "Automated detection of proliferative retinopathy in clinical practice". Clinical Ophthalmology 2 (1): 109–122. doi:10.2147/OPTH.S1579. PMID 19668394.
- ↑ Jump up to: 24.0 24.1 24.2 24.3 Losa, Gabriele A.; Nonnenmacher, Theo F. (2005). Fractals in biology and medicine. Springer. ISBN 978-3-7643-7172-2. https://books.google.com/books?id=t9l9GdAt95gC.
- ↑ Jump up to: 25.0 25.1 25.2 Vannucchi, Paola; Leoni, Lorenzo (2007). "Structural characterization of the Costa Rica décollement: Evidence for seismically-induced fluid pulsing". Earth and Planetary Science Letters 262 (3–4): 413. doi:10.1016/j.epsl.2007.07.056. Bibcode: 2007E&PSL.262..413V.
- ↑ Jump up to: 26.0 26.1 Wallace, David Foster (August 4, 2006). "Bookworm on KCRW". Kcrw.com. http://www.kcrw.com/etc/programs/bw/bw960411david_foster_wallace.
- ↑ Jump up to: 27.0 27.1 Eglash, Ron (1999). "African Fractals: Modern Computing and Indigenous Design". New Brunswick: Rutgers University Press. http://www.rpi.edu/~eglash/eglash.dir/afractal/afractal.htm.
- ↑ Jump up to: 28.0 28.1 Ostwald, Michael J., and Vaughan, Josephine (2016) The Fractal Dimension of Architecture Birhauser, Basel. doi:10.1007/978-3-319-32426-5.
- ↑ Baranger, Michael. "Chaos, Complexity, and Entropy: A physics talk for non-physicists". http://necsi.edu/projects/baranger/cce.pdf.
- ↑ Benoît Mandelbrot, Objets fractals, 1975, p. 4
- ↑ Jump up to: 31.0 31.1 31.2 31.3 Albers, Donald J.; Alexanderson, Gerald L. (2008). "Benoît Mandelbrot: In his own words". Mathematical people : profiles and interviews. Wellesley, MA: AK Peters. p. 214. ISBN 978-1-56881-340-0.
- ↑ fractal (3rd ed.), Oxford University Press, September 2005, http://www.oed.com/view/Entry/74094 (Subscription or UK public library membership required.)
- ↑ Jump up to: 33.0 33.1 33.2 33.3 Gordon, Nigel (2000). Introducing fractal geometry. Duxford: Icon. p. 71. ISBN 978-1-84046-123-7. https://archive.org/details/introducingfract0000lesm/page/71.
- ↑ Eglash, Ron (1999). African Fractals Modern Computing and Indigenous Design. Rutgers University Press. ISBN 978-0-8135-2613-3.
- ↑ Jump up to: 35.0 35.1 Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. Sterling. p. 310. ISBN 978-1-4027-5796-9. https://books.google.com/books?id=JrslMKTgSZwC&q=fractal+koch+curve+book&pg=PA310.
- ↑ "Fractal Geometry". http://www-history.mcs.st-and.ac.uk/HistTopics/fractals.html.
- ↑ Mandelbrot, B. (1967). "How Long Is the Coast of Britain?". Science 156 (3775): 636–638. doi:10.1126/science.156.3775.636. PMID 17837158. Bibcode: 1967Sci...156..636M. http://ena.lp.edu.ua:8080/handle/ntb/52473. Retrieved October 31, 2020.
- ↑ Batty, Michael (April 4, 1985). "Fractals – Geometry Between Dimensions". New Scientist 105 (1450): 31. https://books.google.com/books?id=sz6GAq_PsmMC&pg=PA31.
- ↑ Russ, John C. (1994). Fractal surfaces. 1. Springer. p. 1. ISBN 978-0-306-44702-0. https://books.google.com/books?id=qDQjyuuDRxUC&pg=PA1. Retrieved February 5, 2011.
- ↑ "Vol Libre, an amazing CG film from 1980" (in en). https://kottke.org/09/07/vol-libre-an-amazing-cg-film-from-1980.
- ↑ Edgar, Gerald (2008). Measure, topology, and fractal geometry. New York: Springer-Verlag. p. 1. ISBN 978-0-387-74748-4.
- ↑ Karperien, Audrey (2004). Defining microglial morphology: Form, Function, and Fractal Dimension. Charles Sturt University. doi:10.13140/2.1.2815.9048.
- ↑ Spencer, John; Thomas, Michael S. C.; McClelland, James L. (2009). Toward a unified theory of development : connectionism and dynamic systems theory re-considered. Oxford/New York: Oxford University Press. ISBN 978-0-19-530059-8.
- ↑ Frame, Angus (August 3, 1998). "Iterated Function Systems". in Pickover, Clifford A.. Chaos and fractals: a computer graphical journey : ten year compilation of advanced research. Elsevier. pp. 349–351. ISBN 978-0-444-50002-1. https://books.google.com/books?id=A51ARsapVuUC. Retrieved February 4, 2012.
- ↑ "Haferman Carpet". WolframAlpha. http://www.wolframalpha.com/input/?i=Haferman+carpet.
- ↑ Jump up to: 46.0 46.1 46.2 46.3 Hahn, Horst K.; Georg, Manfred; Peitgen, Heinz-Otto (2005). "Fractal aspects of three-dimensional vascular constructive optimization". in Losa, Gabriele A.; Nonnenmacher, Theo F.. Fractals in biology and medicine. Springer. pp. 55–66. ISBN 978-3-7643-7172-2. https://books.google.com/books?id=t9l9GdAt95gC.
- ↑ J. W. Cannon, W. J. Floyd, W. R. Parry. Finite subdivision rules. Conformal Geometry and Dynamics, vol. 5 (2001), pp. 153–196.
- ↑ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw (2000) (in en). Pattern Formation in Biology, Vision and Dynamics. World Scientific. ISBN 978-981-02-3792-9. https://books.google.com/books?id=qZHyqUli9y8C&dq=%2522james+w.+cannon%2522+maths&pg=PA65.
- ↑ Fathallah-Shaykh, Hassan M. (2011). "Fractal Dimension of the Drosophila Circadian Clock". Fractals 19 (4): 423–430. doi:10.1142/S0218348X11005476.
- ↑ "Hunting the Hidden Dimensional". Nova. PBS. WPMB-Maryland. October 28, 2008.
- ↑ Sadegh, Sanaz (2017). "Plasma Membrane is Compartmentalized by a Self-Similar Cortical Actin Meshwork". Physical Review X 7 (1): 011031. doi:10.1103/PhysRevX.7.011031. PMID 28690919. Bibcode: 2017PhRvX...7a1031S.
- ↑ Falconer, Kenneth (2013). Fractals, A Very Short Introduction. Oxford University Press.
- ↑ Lovejoy, Shaun (1982). "Area-perimeter relation for rain and cloud areas". Science 216 (4542): 185–187. doi:10.1126/science.216.4542.185. PMID 17736252. Bibcode: 1982Sci...216..185L.
- ↑ Cannon, James W.; Floyd, William J.; Perry, Walter R. (2000). "Crystal growth, biological cell growth and geometry". Pattern formation in biology, vision and dynamics. World Scientific. pp. 65–82. ISBN 978-981-02-3792-9. https://books.google.com/books?id=qZHyqUli9y8C&q=crystal+fractals+book&pg=PA78.
- ↑ Singh, Chamkor; Mazza, Marco (2019), "Electrification in granular gases leads to constrained fractal growth", Scientific Reports (Nature Publishing Group) 9 (1): 9049, doi:10.1038/s41598-019-45447-x, PMID 31227758, Bibcode: 2019NatSR...9.9049S
- ↑ Sornette, Didier (2004). Critical phenomena in natural sciences: chaos, fractals, selforganization, and disorder: concepts and tools. Springer. pp. 128–140. ISBN 978-3-540-40754-6.
- ↑ Jump up to: 57.0 57.1 57.2 Sweet, D.; Ott, E.; Yorke, J. A. (1999), "Complex topology in Chaotic scattering: A Laboratory Observation", Nature 399 (6734): 315, doi:10.1038/20573, Bibcode: 1999Natur.399..315S
- ↑ D. Seekell; B. Cael; E. Lindmark; P. Byström (2021). "The fractal scaling relationship for river inlets to lakes". Geophysical Research Letters 48 (9): e2021GL093366. doi:10.1029/2021GL093366. ISSN 0094-8276. Bibcode: 2021GeoRL..4893366S. http://urn.kb.se/resolve?urn=urn:nbn:se:umu:diva-183511.
- ↑ D. Seekell; M. L. Pace; L. J. Tranvik; C. Verpoorter (2013). "A fractal-based approach to lake size-distributions". Geophysical Research Letters 40 (3): 517–521. doi:10.1002/grl.50139. Bibcode: 2013GeoRL..40..517S. https://hal.archives-ouvertes.fr/hal-00932495/file/grl.50139.pdf.
- ↑ B. B. Cael; D. A. Seekell (2016). "The size-distribution of Earth's lakes". Scientific Reports 6: 29633. doi:10.1038/srep29633. PMID 27388607. Bibcode: 2016NatSR...629633C.
- ↑ Addison, Paul S. (1997). Fractals and chaos: an illustrated course. CRC Press. pp. 44–46. ISBN 978-0-7503-0400-9. https://books.google.com/books?id=l2E4ciBQ9qEC&q=lightning+fractals+book&pg=PA45. Retrieved February 5, 2011.
- ↑ Enright, Matthew B.; Leitner, David M. (January 27, 2005). "Mass fractal dimension and the compactness of proteins". Physical Review E 71 (1): 011912. doi:10.1103/PhysRevE.71.011912. PMID 15697635. Bibcode: 2005PhRvE..71a1912E. https://zenodo.org/record/895378.
- ↑ Takeda, T; Ishikawa, A; Ohtomo, K; Kobayashi, Y; Matsuoka, T (February 1992). "Fractal dimension of dendritic tree of cerebellar Purkinje cell during onto- and phylogenetic development". Neurosci Research 13 (1): 19–31. doi:10.1016/0168-0102(92)90031-7. PMID 1314350.
- ↑ Takayasu, H. (1990). Fractals in the physical sciences. Manchester: Manchester University Press. p. 36. ISBN 978-0-7190-3434-3. https://archive.org/details/fractalsinphysic0000taka_s1f9/page/36.
- ↑ Jun, Li; Ostoja-Starzewski, Martin (April 1, 2015). "Edges of Saturn's Rings are Fractal". SpringerPlus 4,158: 158. doi:10.1186/s40064-015-0926-6. PMID 25883885.
- ↑ Meyer, Yves; Roques, Sylvie (1993). Progress in wavelet analysis and applications: proceedings of the International Conference "Wavelets and Applications", Toulouse, France – June 1992. Atlantica Séguier Frontières. p. 25. ISBN 978-2-86332-130-0. https://books.google.com/books?id=aHux78oQbbkC&q=snowflake+fractals+book&pg=PA25. Retrieved February 5, 2011.
- ↑ Ozhovan M. I., Dmitriev I. E., Batyukhnova O. G. Fractal structure of pores of clay soil. Atomic Energy, 74, 241–243 (1993).
- ↑ Sreenivasan, K. R.; Meneveau, C. (1986). "The Fractal Facets of Turbulence". Journal of Fluid Mechanics 173: 357–386. doi:10.1017/S0022112086001209. Bibcode: 1986JFM...173..357S.
- ↑ de Silva, C. M.; Philip, J.; Chauhan, K.; Meneveau, C.; Marusic, I. (2013). "Multiscale Geometry and Scaling of the Turbulent–Nonturbulent Interface in High Reynolds Number Boundary Layers". Phys. Rev. Lett. 111 (6039): 192–196. doi:10.1126/science.1203223. PMID 21737736. Bibcode: 2011Sci...333..192A.
- ↑ Leggett, Susan E.; Neronha, Zachary J.; Bhaskar, Dhananjay; Sim, Jea Yun; Perdikari, Theodora Myrto; Wong, Ian Y. (2019-08-27). "Motility-limited aggregation of mammary epithelial cells into fractal-like clusters" (in en). Proceedings of the National Academy of Sciences 116 (35): 17298–17306. doi:10.1073/pnas.1905958116. ISSN 0027-8424. PMID 31413194. Bibcode: 2019PNAS..11617298L.
- ↑ Jelinek, Herbert F; Fernandez, Eduardo (June 1998). "Neurons and fractals: how reliable and useful are calculations of fractal dimensions?" (in en). Journal of Neuroscience Methods 81 (1–2): 9–18. doi:10.1016/S0165-0270(98)00021-1. PMID 9696304. https://linkinghub.elsevier.com/retrieve/pii/S0165027098000211.
- ↑ Cross, Simon S. (1997). "Fractals in Pathology" (in en). The Journal of Pathology 182 (1): 1–8. doi:10.1002/(SICI)1096-9896(199705)182:1<1::AID-PATH808>3.0.CO;2-B. ISSN 1096-9896. PMID 9227334.
- ↑ Speckner, Konstantin; Stadler, Lorenz; Weiss, Matthias (2018-07-09). "Anomalous dynamics of the endoplasmic reticulum network" (in en). Physical Review E 98 (1): 012406. doi:10.1103/PhysRevE.98.012406. ISSN 2470-0045. PMID 30110830. Bibcode: 2018PhRvE..98a2406S. https://link.aps.org/doi/10.1103/PhysRevE.98.012406.
- ↑ Taylor, R. P. (1999). "Fractal Analysis of Pollock's Drip Paintings". Nature 399 (6735): 422. doi:10.1038/20833. Bibcode: 1999Natur.399..422T.
- ↑ Taylor, R. P. (2006). "Fractal Analysis: Revisiting Pollock's Paintings (Reply)". Nature 444 (7119): E10–11. doi:10.1038/nature05399. Bibcode: 2006Natur.444E..10T.
- ↑ Lee, S.; Olsen, S.; Gooch, B. (2007). "Simulating and Analyzing Jackson Pollock's Paintings". Journal of Mathematics and the Arts 1 (2): 73–83. doi:10.1080/17513470701451253.
- ↑ Shamar, L. (2015). "What Makes a Pollock Pollock: A Machine Vision Approach". International Journal of Arts and Technology 8: 1–10. doi:10.1504/IJART.2015.067389. http://vfacstaff.ltu.edu/lshamir/publications/wm_pollock.pdf. Retrieved October 24, 2017.
- ↑ Taylor, R. P.; Spehar, B.; Van Donkelaar, P.; Hagerhall, C. M. (2011). "Perceptual and Physiological Responses to Jackson Pollock's Fractals". Frontiers in Human Neuroscience 5: 1–13. doi:10.3389/fnhum.2011.00060. PMID 21734876.
- ↑ Frame, Michael; and Mandelbrot, Benoît B.; A Panorama of Fractals and Their Uses
- ↑ Nelson, Bryn (2000-02-23). "Sophisticated Mathematics Behind African Village Designs / Fractal patterns use repetition on large, small scale" (in en-US). https://www.sfgate.com/education/article/Sophisticated-Mathematics-Behind-African-Village-2774181.php.
- ↑ Situngkir, Hokky; Dahlan, Rolan (2009). Fisika batik: implementasi kreatif melalui sifat fraktal pada batik secara komputasional. Jakarta: Gramedia Pustaka Utama. ISBN:978-979-22-4484-7
- ↑ Rulistia, Novia D. (October 6, 2015). "Application maps out nation's batik story". The Jakarta Post. http://www.thejakartapost.com/news/2015/10/06/application-maps-out-nation-s-batik-story.html.
- ↑ Koutonin, Mawuna (March 18, 2016). "Story of cities #5: Benin City, the mighty medieval capital now lost without trace". Retrieved April 2, 2018.
- ↑ Robles, Kelly E.; Roberts, Michelle; Viengkham, Catherine; Smith, Julian H.; Rowland, Conor; Moslehi, Saba; Stadlober, Sabrina; Lesjak, Anastasija et al. (2021). "Aesthetics and Psychological Effects of Fractal Based Design". Frontiers in Psychology 12. doi:10.3389/fpsyg.2021.699962. ISSN 1664-1078. PMID 34484047.
- ↑ Taylor, Richard P. (2016). "Fractal Fluency: An Intimate Relationship Between the Brain and Processing of Fractal Stimuli". in Di Ieva, Antonio. The Fractal Geometry of the Brain. Springer Series in Computational Neuroscience. Springer. pp. 485–496. ISBN 978-1-4939-3995-4.
- ↑ Taylor, Richard P. (2006). "Reduction of Physiological Stress Using Fractal Art and Architecture". Leonardo 39 (3): 245–251. doi:10.1162/leon.2006.39.3.245. https://zenodo.org/record/894740.
- ↑ For further discussion of this effect, see Taylor, Richard P.; Spehar, Branka; Donkelaar, Paul Van; Hagerhall, Caroline M. (2011). "Perceptual and Physiological Responses to Jackson Pollock's Fractals". Frontiers in Human Neuroscience 5: 60. doi:10.3389/fnhum.2011.00060. PMID 21734876.
- ↑ Hohlfeld, Robert G.; Cohen, Nathan (1999). "Self-similarity and the geometric requirements for frequency independence in Antennae". Fractals 7 (1): 79–84. doi:10.1142/S0218348X99000098.
- ↑ Reiner, Richard; Waltereit, Patrick; Benkhelifa, Fouad; Müller, Stefan; Walcher, Herbert; Wagner, Sandrine; Quay, Rüdiger; Schlechtweg, Michael et al. (2012). "Fractal structures for low-resistance large area AlGaN/GaN power transistors". 2012 24th International Symposium on Power Semiconductor Devices and ICs. pp. 341–344. doi:10.1109/ISPSD.2012.6229091. ISBN 978-1-4577-1596-9.
- ↑ "Review of Fractal Heat Exchangers" (PDF). 2016. http://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=2724&context=iracc International Refrigeration and Air Conditioning Conference. Paper 1725
- ↑ Chen, Yanguang (2011). "Modeling Fractal Structure of City-Size Distributions Using Correlation Functions". PLOS ONE 6 (9): e24791. doi:10.1371/journal.pone.0024791. PMID 21949753. Bibcode: 2011PLoSO...624791C.
- ↑ "Applications". http://library.thinkquest.org/26242/full/ap/ap.html.
- ↑ Azua-Bustos, Armando; Vega-Martínez, Cristian (October 2013). ""Detecting 'life as we don't know it' by fractal analysis"". International Journal of Astrobiology 12 (4): 314–320. doi:10.1017/S1473550413000177. http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=9012687&fileId=S1473550413000177.
- ↑ Smith, Robert F.; Mohr, David N.; Torres, Vicente E.; Offord, Kenneth P.; Melton III, L. Joseph (1989). "Renal insufficiency in community patients with mild asymptomatic microhematuria". Mayo Clinic Proceedings 64 (4): 409–414. doi:10.1016/s0025-6196(12)65730-9. PMID 2716356.
- ↑ Landini, Gabriel (2011). "Fractals in microscopy". Journal of Microscopy 241 (1): 1–8. doi:10.1111/j.1365-2818.2010.03454.x. PMID 21118245.
- ↑ Cheng, Qiuming (1997). "Multifractal Modeling and Lacunarity Analysis". Mathematical Geology 29 (7): 919–932. doi:10.1023/A:1022355723781.
- ↑ Chen, Yanguang (2011). "Modeling Fractal Structure of City-Size Distributions Using Correlation Functions". PLOS ONE 6 (9): e24791. doi:10.1371/journal.pone.0024791. PMID 21949753. Bibcode: 2011PLoSO...624791C.
- ↑ Burkle-Elizondo, Gerardo; Valdéz-Cepeda, Ricardo David (2006). "Fractal analysis of Mesoamerican pyramids". Nonlinear Dynamics, Psychology, and Life Sciences 10 (1): 105–122. PMID 16393505.
- ↑ Brown, Clifford T.; Witschey, Walter R. T.; Liebovitch, Larry S. (2005). "The Broken Past: Fractals in Archaeology". Journal of Archaeological Method and Theory 12: 37–78. doi:10.1007/s10816-005-2396-6.
- ↑ Saeedi, Panteha; Sorensen, Soren A. (2009). "An Algorithmic Approach to Generate After-disaster Test Fields for Search and Rescue Agents". Proceedings of the World Congress on Engineering 2009: 93–98. ISBN 978-988-17-0125-1. http://www.iaeng.org/publication/WCE2009/WCE2009_pp93-98.pdf.
- ↑ "GPU internals". http://fileadmin.cs.lth.se/cs/Personal/Michael_Doggett/pubs/doggett12-tc.pdf.
- ↑ "sony patents". https://www.google.ch/patents/US20150287166?dq=morton+order+texture+swizzling.
- ↑ "description of swizzled and hybrid tiled swizzled textures". https://news.ycombinator.com/item?id=2239173.
- ↑ "US8773422B1 - System, method, and computer program product for grouping linearly ordered primitives". December 4, 2007. http://www.google.com/patents/US8773422.
- ↑ "US20110227921A1 - Processing of 3D computer graphics data on multiple shading engines". December 15, 2010. http://www.google.ch/patents/US20110227921.
- ↑ "Johns Hopkins Turbulence Databases". http://turbulence.pha.jhu.edu.
- ↑ Li, Y.; Perlman, E.; Wang, M.; Yang, y.; Meneveau, C.; Burns, R.; Chen, S.; Szalay, A. et al. (2008). "A Public Turbulence Database Cluster and Applications to Study Lagrangian Evolution of Velocity Increments in Turbulence". Journal of Turbulence 9: N31. doi:10.1080/14685240802376389. Bibcode: 2008JTurb...9...31L.
Further reading
- Barnsley, Michael F.; and Rising, Hawley; Fractals Everywhere. Boston: Academic Press Professional, 1993. ISBN 0-12-079061-0
- Duarte, German A.; Fractal Narrative. About the Relationship Between Geometries and Technology and Its Impact on Narrative Spaces. Bielefeld: Transcript, 2014. ISBN 978-3-8376-2829-6
- Falconer, Kenneth; Techniques in Fractal Geometry. John Wiley and Sons, 1997. ISBN 0-471-92287-0
- Jürgens, Hartmut; Peitgen, Heinz-Otto; and Saupe, Dietmar; Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, 1992. ISBN 0-387-97903-4
- Mandelbrot, Benoit B.; The Fractal Geometry of Nature. New York: W. H. Freeman and Co., 1982. ISBN 0-7167-1186-9
- Peitgen, Heinz-Otto; and Saupe, Dietmar; eds.; The Science of Fractal Images. New York: Springer-Verlag, 1988. ISBN 0-387-96608-0
- Pickover, Clifford A.; ed.; Chaos and Fractals: A Computer Graphical Journey – A 10 Year Compilation of Advanced Research. Elsevier, 1998. ISBN 0-444-50002-2
- Jones, Jesse; Fractals for the Macintosh, Waite Group Press, Corte Madera, CA, 1993. ISBN 1-878739-46-8.
- Lauwerier, Hans; Fractals: Endlessly Repeated Geometrical Figures, Translated by Sophia Gill-Hoffstadt, Princeton University Press, Princeton NJ, 1991. ISBN 0-691-08551-X, cloth. ISBN 0-691-02445-6 paperback. "This book has been written for a wide audience..." Includes sample BASIC programs in an appendix.
- Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 978-0-19-850839-7.
- Wahl, Bernt; Van Roy, Peter; Larsen, Michael; and Kampman, Eric; Exploring Fractals on the Macintosh, Addison Wesley, 1995. ISBN 0-201-62630-6
- Lesmoir-Gordon, Nigel; The Colours of Infinity: The Beauty, The Power and the Sense of Fractals. 2004. ISBN 1-904555-05-5 (The book comes with a related DVD of the Arthur C. Clarke documentary introduction to the fractal concept and the Mandelbrot set.)
- Liu, Huajie; Fractal Art, Changsha: Hunan Science and Technology Press, 1997, ISBN 9787535722348.
- Gouyet, Jean-François; Physics and Fractal Structures (Foreword by B. Mandelbrot); Masson, 1996. ISBN 2-225-85130-1, and New York: Springer-Verlag, 1996. ISBN 978-0-387-94153-0. Out-of-print. Available in PDF version at."Physics and Fractal Structures" (in fr). Jfgouyet.fr. http://www.jfgouyet.fr/fractal/fractauk.html.
- Falconer, Kenneth (2013). Fractals, A Very Short Introduction. Oxford University Press.
External links
| Wikimedia Commons has media related to Fractal. |
- "Hunting the Hidden Dimension", PBS NOVA, first aired August 24, 2011
- Benoit Mandelbrot: Fractals and the Art of Roughness (), TED, February 2010
- Technical Library on Fractals for controlling fluid
- Equations of self-similar fractal measure based on the fractional-order calculus(2007)
 |