Limiting parallel
In neutral or absolute geometry, and in hyperbolic geometry, there may be many lines parallel to a given line [math]\displaystyle{ l }[/math] through a point [math]\displaystyle{ P }[/math] not on line [math]\displaystyle{ R }[/math]; however, in the plane, two parallels may be closer to [math]\displaystyle{ l }[/math] than all others (one in each direction of [math]\displaystyle{ R }[/math]).
Thus it is useful to make a new definition concerning parallels in neutral geometry. If there are closest parallels to a given line they are known as the limiting parallel, asymptotic parallel or horoparallel (horo from Greek: ὅριον — border).
For rays, the relation of limiting parallel is an equivalence relation, which includes the equivalence relation of being coterminal.
If, in a hyperbolic triangle, the pairs of sides are limiting parallel, then the triangle is an ideal triangle.
Definition
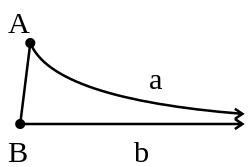
A ray [math]\displaystyle{ Aa }[/math] is a limiting parallel to a ray [math]\displaystyle{ Bb }[/math] if they are coterminal or if they lie on distinct lines not equal to the line [math]\displaystyle{ AB }[/math], they do not meet, and every ray in the interior of the angle [math]\displaystyle{ BAa }[/math] meets the ray [math]\displaystyle{ Bb }[/math].[1]
Properties
Distinct lines carrying limiting parallel rays do not meet.
Proof
Suppose that the lines carrying distinct parallel rays met. By definition they cannot meet on the side of [math]\displaystyle{ AB }[/math] which either [math]\displaystyle{ a }[/math] is on. Then they must meet on the side of [math]\displaystyle{ AB }[/math] opposite to [math]\displaystyle{ a }[/math], call this point [math]\displaystyle{ C }[/math]. Thus [math]\displaystyle{ \angle CAB + \angle CBA \lt 2 \text{ right angles} \Rightarrow \angle aAB + \angle bBA \gt 2 \text{ right angles} }[/math]. Contradiction.
See also
- horocycle, In Hyperbolic geometry a curve whose normals are limiting parallels
- angle of parallelism
References
- ↑ Hartshorne, Robin (2000). Geometry: Euclid and beyond (Corr. 2nd print. ed.). New York, NY [u.a.]: Springer. ISBN 978-0-387-98650-0.
 |