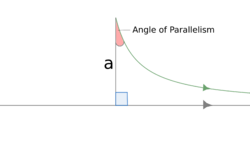
Angle of parallelism
In hyperbolic geometry, angle of parallelism [math]\displaystyle{ \Pi(a) }[/math] is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.
Given a point not on a line, drop a perpendicular to the line from the point. Let a be the length of this perpendicular segment, and [math]\displaystyle{ \Pi(a) }[/math] be the least angle such that the line drawn through the point does not intersect the given line. Since two sides are asymptotically parallel,
- [math]\displaystyle{ \lim_{a\to 0} \Pi(a) = \tfrac{1}{2}\pi\quad\text{ and }\quad\lim_{a\to\infty} \Pi(a) = 0. }[/math]
There are five equivalent expressions that relate [math]\displaystyle{ \Pi(a) }[/math] and a:
- [math]\displaystyle{ \sin\Pi(a) = \operatorname{sech} a = \frac{1}{\cosh a} =\frac{2}{e^a + e^{-a}} \ , }[/math]
- [math]\displaystyle{ \cos\Pi(a) = \tanh a = \frac {e^a - e^{-a}} {e^a + e^{-a}} \ , }[/math]
- [math]\displaystyle{ \tan\Pi(a) = \operatorname{csch} a = \frac{1}{\sinh a} = \frac {2}{e^a - e^{-a}} \ , }[/math]
- [math]\displaystyle{ \tan \left( \tfrac{1}{2}\Pi(a) \right) = e^{-a}, }[/math]
- [math]\displaystyle{ \Pi(a) = \tfrac{1}{2}\pi - \operatorname{gd}(a), }[/math]
where sinh, cosh, tanh, sech and csch are hyperbolic functions and gd is the Gudermannian function.
Construction
János Bolyai discovered a construction which gives the asymptotic parallel s to a line r passing through a point A not on r.[1] Drop a perpendicular from A onto B on r. Choose any point C on r different from B. Erect a perpendicular t to r at C. Drop a perpendicular from A onto D on t. Then length DA is longer than CB, but shorter than CA. Draw a circle around C with radius equal to DA. It will intersect the segment AB at a point E. Then the angle BEC is independent of the length BC, depending only on AB; it is the angle of parallelism. Construct s through A at angle BEC from AB.
- [math]\displaystyle{ \sin BEC = \frac{ \sinh {BC} }{ \sinh {CE} } = \frac{ \sinh {BC} }{ \sinh {DA} } = \frac{ \sinh {BC} }{ \sin {ACD} \sinh {CA} } = \frac{ \sinh {BC} }{ \cos {ACB} \sinh {CA} } = \frac{ \sinh {BC} \tanh {CA} }{ \tanh {CB} \sinh {CA} } = \frac{ \cosh {BC} }{ \cosh {CA} } = \frac{ \cosh {BC} }{ \cosh {CB} \cosh {AB} } = \frac{ 1 }{ \cosh {AB} } \,. }[/math]
See Trigonometry of right triangles for the formulas used here.
History
The angle of parallelism was developed in 1840 in the German publication "Geometrische Untersuchungen zur Theory der Parallellinien" by Nikolai Lobachevsky.
This publication became widely known in English after the Texas professor G. B. Halsted produced a translation in 1891. (Geometrical Researches on the Theory of Parallels)
The following passages define this pivotal concept in hyperbolic geometry:
- The angle HAD between the parallel HA and the perpendicular AD is called the parallel angle (angle of parallelism) which we will here designate by Π(p) for AD = p.[2]:13[3]
Demonstration

This diagram, with yellow ideal triangle, is similar to one found in a book by Smogorzhevsky.[4]
In the Poincaré half-plane model of the hyperbolic plane (see Hyperbolic motions), one can establish the relation of Φ to a with Euclidean geometry. Let Q be the semicircle with diameter on the x-axis that passes through the points (1,0) and (0,y), where y > 1. Since Q is tangent to the unit semicircle centered at the origin, the two semicircles represent parallel hyperbolic lines. The y-axis crosses both semicircles, making a right angle with the unit semicircle and a variable angle Φ with Q. The angle at the center of Q subtended by the radius to (0, y) is also Φ because the two angles have sides that are perpendicular, left side to left side, and right side to right side. The semicircle Q has its center at (x, 0), x < 0, so its radius is 1 − x. Thus, the radius squared of Q is
- [math]\displaystyle{ x^2 + y^2 = (1 - x)^2, }[/math]
hence
- [math]\displaystyle{ x = \tfrac{1}{2}(1 - y^2). }[/math]
The metric of the Poincaré half-plane model of hyperbolic geometry parametrizes distance on the ray {(0, y) : y > 0 } with logarithmic measure. Let log y = a, so y = ea where e is the base of the natural logarithm. Then the relation between φ and a can be deduced from the triangle {(x, 0), (0, 0), (0, y)}, for example:
- [math]\displaystyle{ \tan\phi = \frac{y}{-x} = \frac{2y}{y^2 - 1} = \frac{2e^a}{e^{2a} - 1} = \frac{1}{\sinh a}. }[/math]
References
- ↑ "Non-Euclidean Geometry" by Roberto Bonola, page 104, Dover Publications.
- ↑ Nikolai Lobachevsky (1840) G. B. Halsted translator (1891) Geometrical Researches on the Theory of Parallels
- ↑ Bonola, Roberto (1955). Non-Euclidean geometry : a critical and historical study of its developments (Unabridged and unaltered republ. of the 1. English translation 1912. ed.). New York, NY: Dover. ISBN 0-486-60027-0. https://archive.org/details/noneuclideangeom0000bono.
- ↑ A.S. Smogorzhevsky (1982) Lobachevskian Geometry, §12 Basic formulas of hyperbolic geometry, figure 37, page 60, Mir Publishers, Moscow
- Marvin J. Greenberg (1974) Euclidean and Non-Euclidean Geometries, pp. 211–3, W.H. Freeman & Company.
- Robin Hartshorne (1997) Companion to Euclid pp. 319, 325, American Mathematical Society, ISBN:0821807978.
- Jeremy Gray (1989) Ideas of Space: Euclidean, Non-Euclidean, and Relativistic, 2nd edition, Clarendon Press, Oxford (See pages 113 to 118).
- Béla Kerékjártó (1966) Les Fondements de la Géométry, Tome Deux, §97.6 Angle de parallélisme de la géométry hyperbolique, pp. 411,2, Akademiai Kiado, Budapest.
 |