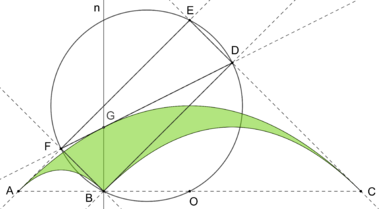
Parbelos
The parbelos is a figure similar to the arbelos but instead of three half circles it uses three parabola segments. More precisely the parbelos consists of three parabola segments, that have a height that is one fourth of the width at their bases. The two smaller parabola segments are placed next to each other with their bases on a common line and the largest parabola is placed over the two smaller ones such that its width is the sum of the widths of the smaller ones (see graphic).
The parbelos has a number of properties which are somewhat similar or even identical to the properties of the Arbelos. For instance, the following two properties are identical to those of the arbelos:[1]
- The arc length of the outer parabola is equal to the sum of the arc lengths of the inner parabolas.
- In a nested arbelos construction with the inner parabola segments being arbeloses themselves the two innermost parabola segments being adjacent to the cusp of the outer arbelos are congruent, that is of equal size.
The quadrilateral [math]\displaystyle{ BM_2MM_1 }[/math] formed by the inner cusp [math]\displaystyle{ B }[/math] and the midpoints [math]\displaystyle{ M, M_1, M_2 }[/math] of the three parabola arcs is a parallelogram the area of which relates to the area of the parbelos as follows:[1]
- [math]\displaystyle{ F_{\text{parallelogram}}=\frac{3}{4}F_{\text{parbelos}} }[/math]
The four tangents at the three cusps of the parabola intersect in four points, which form a rectangle being called the tangent rectangle. The circumcircle of the tangent rectangle intersects the base side of the outer parabola segment in its midpoint, which is the focus of the outer parabola. One diagonal of the tangent rectangle lies on a tangent to the outer parabola and its common point with it is identical to its point of intersection with perpendicular to the base at the inner cusp. For the area of the tangent rectangle the following equation holds:[2]
- [math]\displaystyle{ F_{\text{rectangle}}=\frac{3}{2}F_{\text{parbelos}} }[/math]
References
- ↑ 1.0 1.1 Michał Różański, Alicja Samulewicz, Marcin Szweda, Roman Wituła: "Variations on the arbelos". In: Journal of Applied Mathematics and Computational Mechanics, Volume 16, Issue 2, 2017, pp. 123-133 (online copy)
- ↑ Jonathan Sondow: "The Parbelos, a Parabolic Analog of the Arbelos". In: The American Mathematical Monthly, Vol. 120, No. 10 (December 2013), pp. 929-935 (JSTOR)
Further reading
- Emmanuel Tsukerman: "Solution of Sondow’s Problem: A Synthetic Proof of the Tangency Property of the Parbelos". In: The American Mathematical Monthly** , Vol. 121, No. 5 (May 2014), pp. 438-443
- Antonio M. Oller-Marcén: "The f-belos". In: Forum Geometricorum, 13 (2013), pp. 103-111 (online copy)
- Viktorija Ternar: Arbelos, parabelos in f-belos (master thesis, University of Maribor, 2015)
 |