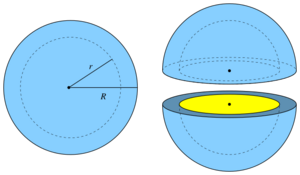
Spherical shell
From HandWiki
In geometry, a spherical shell is a generalization of an annulus to three dimensions. It is the region of a ball between two concentric spheres of differing radii.[1]
Volume
The volume of a spherical shell is the difference between the enclosed volume of the outer sphere and the enclosed volume of the inner sphere:
- [math]\displaystyle{ \begin{align} V &= \tfrac43\pi R^3 - \tfrac43\pi r^3 \\[3mu] &= \tfrac43\pi \bigl(R^3 - r^3\bigr) \\[3mu] &= \tfrac43\pi (R-r)\bigl(R^2 + Rr + r^2\bigr) \end{align} }[/math]
where r is the radius of the inner sphere and R is the radius of the outer sphere.
Approximation
An approximation for the volume of a thin spherical shell is the surface area of the inner sphere multiplied by the thickness t of the shell:[2]
- [math]\displaystyle{ V \approx 4 \pi r^2 t, }[/math]
when t is very small compared to r ([math]\displaystyle{ t \ll r }[/math]).
The total surface area of the spherical shell is [math]\displaystyle{ 4 \pi r^2 }[/math].
See also
References
- ↑ Weisstein, Eric W.. "Spherical Shell" (in en). Wolfram Research, Inc.. http://mathworld.wolfram.com/SphericalShell.html.
- ↑ Znamenski, Andrey Varlamov; Lev Aslamazov (2012). A.A. Abrikosov Jr.. ed. The wonders of physics (3rd ed.). Singapore: World Scientific. p. 78. ISBN 978-981-4374-15-6. https://books.google.com/books?id=xh48DQAAQBAJ&pg=PA78.
 |