Annulus (mathematics)

Short description: Region between two concentric circles

Illustration of Mamikon's visual calculus method showing that the areas of two annuli with the same chord length are the same regardless of inner and outer radii.

In mathematics, an annulus (pl.: annuli or annuluses) is the region between two concentric circles. Informally, it is shaped like a ring or a hardware washer. The word "annulus" is borrowed from the Latin word anulus or annulus meaning 'little ring'. The adjectival form is annular (as in annular eclipse).

The open annulus is topologically equivalent to both the open cylinder S¹ × (0,1) and the punctured plane.

Area

The area of an annulus is the difference in the areas of the larger circle of radius R and the smaller one of radius r:

[math]\displaystyle{ A = \pi R^2 - \pi r^2 = \pi\left(R^2 - r^2\right). }[/math]

As a corollary of the chord formula, the area bounded by the circumcircle and incircle of every unit convex regular polygon is π/4

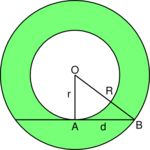
The area of an annulus is determined by the length of the longest line segment within the annulus, which is the chord tangent to the inner circle, 2d in the accompanying diagram. That can be shown using the Pythagorean theorem since this line is tangent to the smaller circle and perpendicular to its radius at that point, so d and r are sides of a right-angled triangle with hypotenuse R, and the area of the annulus is given by

[math]\displaystyle{ A = \pi\left(R^2 - r^2\right) = \pi d^2. }[/math]

The area can also be obtained via calculus by dividing the annulus up into an infinite number of annuli of infinitesimal width dρ and area 2πρ dρ and then integrating from ρ = r to ρ = R:

[math]\displaystyle{ A = \int_r^R\!\! 2\pi\rho\, d\rho = \pi\left(R^2 - r^2\right). }[/math]

The area of an annulus sector of angle θ, with θ measured in radians, is given by

[math]\displaystyle{ A = \frac{\theta}{2} \left(R^2 - r^2\right). }[/math]

Complex structure

In complex analysis an annulus ann(a; r, R) in the complex plane is an open region defined as

[math]\displaystyle{ r \lt |z - a| \lt R. }[/math]

If r is 0, the region is known as the punctured disk (a disk with a point hole in the center) of radius R around the point a.

As a subset of the complex plane, an annulus can be considered as a Riemann surface. The complex structure of an annulus depends only on the ratio r/R. Each annulus ann(a; r, R) can be holomorphically mapped to a standard one centered at the origin and with outer radius 1 by the map

[math]\displaystyle{ z \mapsto \frac{z - a}{R}. }[/math]

The inner radius is then r/R < 1.

The Hadamard three-circle theorem is a statement about the maximum value a holomorphic function may take inside an annulus.

The Joukowsky transform conformally maps an annulus onto an ellipse with a slit cut between foci.

See also

• Engineering:Annular cutter – Form of core drill
• Annulus theorem/conjecture – In mathematics, on the region between two well-behaved spheres
• Spherical shell
• Torus – Doughnut-shaped surface of revolution

External links

• Annulus definition and properties With interactive animation
• Area of an annulus, formula With interactive animation