Isophote
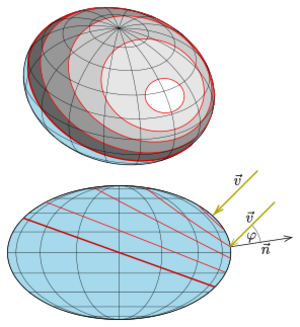
In geometry, an isophote is a curve on an illuminated surface that connects points of equal brightness. One supposes that the illumination is done by parallel light and the brightness b is measured by the following scalar product:
- [math]\displaystyle{ b(P)= \vec n(P)\cdot \vec v=\cos\varphi }[/math]
where [math]\displaystyle{ \vec n(P) }[/math] is the unit normal vector of the surface at point P and [math]\displaystyle{ \vec v }[/math] the unit vector of the light's direction. If b(P) = 0, i.e. the light is perpendicular to the surface normal, then point P is a point of the surface silhouette observed in direction [math]\displaystyle{ \vec v. }[/math] Brightness 1 means that the light vector is perpendicular to the surface. A plane has no isophotes, because every point has the same brightness.
In astronomy, an isophote is a curve on a photo connecting points of equal brightness. [1]
Application and example
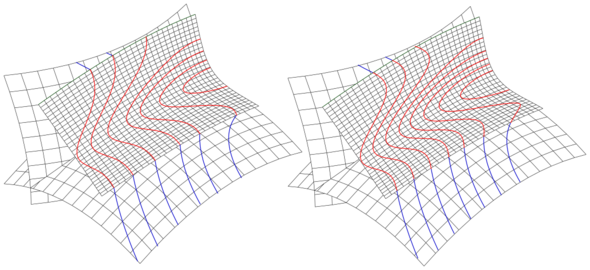
In computer-aided design, isophotes are used for checking optically the smoothness of surface connections. For a surface (implicit or parametric), which is differentiable enough, the normal vector depends on the first derivatives. Hence, the differentiability of the isophotes and their geometric continuity is 1 less than that of the surface. If at a surface point only the tangent planes are continuous (i.e. G1-continuous), the isophotes have there a kink (i.e. is only G0-continuous).
In the following example (s. diagram), two intersecting Bezier surfaces are blended by a third surface patch. For the left picture, the blending surface has only G1-contact to the Bezier surfaces and for the right picture the surfaces have G2-contact. This difference can not be recognized from the picture. But the geometric continuity of the isophotes show: on the left side, they have kinks (i.e. G0-continuity), and on the right side, they are smooth (i.e. G1-continuity).
Determining points of an isophote
On an implicit surface
For an implicit surface with equation [math]\displaystyle{ f(x,y,z)=0, }[/math] the isophote condition is [math]\displaystyle{ \frac{\nabla f \cdot \vec v}{|\nabla f|}= c \ . }[/math] That means: points of an isophote with given parameter c are solutions of the nonlinear system [math]\displaystyle{ \begin{align} f(x,y,z) &= 0, \\[4pt] \nabla f (x,y,z)\cdot \vec v -c\;|\nabla f(x,y,z)| &= 0, \end{align} }[/math] which can be considered as the intersection curve of two implicit surfaces. Using the tracing algorithm of Bajaj et al. (see references) one can calculate a polygon of points.
On a parametric surface
In case of a parametric surface [math]\displaystyle{ \vec x= \vec S(s,t) }[/math] the isophote condition is
[math]\displaystyle{ \frac{(\vec S_s\times\vec S_t)\cdot\vec v}{|\vec S_s\times\vec S_t|}=c\ . }[/math]
which is equivalent to [math]\displaystyle{ \ (\vec S_s\times\vec S_t)\cdot\vec v- c\;|\vec S_s\times\vec S_t|=0 \ . }[/math] This equation describes an implicit curve in the s-t-plane, which can be traced by a suitable algorithm (see implicit curve) and transformed by [math]\displaystyle{ \vec S(s,t) }[/math] into surface points.
See also
References
- J. Hoschek, D. Lasser: Grundlagen der geometrischen Datenverarbeitung, Teubner-Verlag, Stuttgart, 1989, ISBN:3-519-02962-6, p. 31.
- Z. Sun, S. Shan, H. Sang et al.: Biometric Recognition, Springer, 2014, ISBN:978-3-319-12483-4, p. 158.
- C.L. Bajaj, C.M. Hoffmann, R.E. Lynch, J.E.H. Hopcroft: Tracing Surface Intersections, (1988) Comp. Aided Geom. Design 5, pp. 285–307.
- C. T. Leondes: Computer Aided and Integrated Manufacturing Systems: Optimization methods, Vol. 3, World Scientific, 2003, ISBN:981-238-981-4, p. 209.
External links
- Patrikalakis-Maekawa-Cho: Isophotes (engl.)
- A. Diatta, P. Giblin: Geometry of Isophote Curves
- Jin Kim: Computing Isophotes of Surface of Revolution and Canal Surface
 |