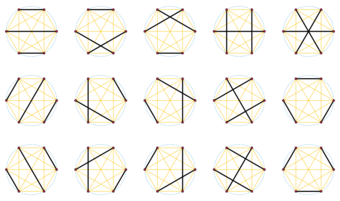
Chord diagram (mathematics)
In mathematics, a chord diagram consists of a cyclic order on a set of objects, together with a one-to-one pairing (perfect matching) of those objects. Chord diagrams are conventionally visualized by arranging the objects in their order around a circle, and drawing the pairs of the matching as chords of the circle.
The number of different chord diagrams that may be given for a set of [math]\displaystyle{ 2n }[/math] cyclically ordered objects is the double factorial [math]\displaystyle{ (2n-1)!! }[/math].[1] There is a Catalan number of chord diagrams on a given ordered set in which no two chords cross each other.[2] The crossing pattern of chords in a chord diagram may be described by a circle graph, the intersection graph of the chords: it has a vertex for each chord and an edge for each two chords that cross.[3]
In knot theory, a chord diagram can be used to describe the sequence of crossings along the planar projection of a knot, with each point at which a crossing occurs paired with the point that crosses it. To fully describe the knot, the diagram should be annotated with an extra bit of information for each pair, indicating which point crosses over and which crosses under at that crossing. With this extra information, the chord diagram of a knot is called a Gauss diagram.[4] In the Gauss diagram of a knot, every chord crosses an even number of other chords, or equivalently each pair in the diagram connects a point in an even position of the cyclic order with a point in an odd position, and sometimes this is used as a defining condition of Gauss diagrams.[5]
In algebraic geometry, chord diagrams can be used to represent the singularities of algebraic plane curves.[6]
See also
References
- ↑ Dale, M. R. T.; Moon, J. W. (1993), "The permuted analogues of three Catalan sets", Journal of Statistical Planning and Inference 34 (1): 75–87, doi:10.1016/0378-3758(93)90035-5
- ↑ Krob, Daniel; Mikhalev, Alexander A.; Mikhalev, Alexander V., eds. (2000), "Analytic combinatorics of chord diagrams", Formal Power Series and Algebraic Combinatorics: 12th International Conference, FPSAC'00, Moscow, Russia, June 2000, Proceedings, Berlin: Springer, pp. 191–201, doi:10.1007/978-3-662-04166-6_17, https://hal.inria.fr/file/index/docid/72739/filename/RR-3914.pdf
- ↑ de Fraysseix, Hubert (1984), "A characterization of circle graphs", European Journal of Combinatorics 5 (3): 223–238, doi:10.1016/S0195-6698(84)80005-0
- ↑ Polyak, Michael (1994), "Gauss diagram formulas for Vassiliev invariants", International Mathematics Research Notices 1994 (11): 445–453, doi:10.1155/S1073792894000486
- ↑ Khan, Abdullah; Lisitsa, Alexei; Vernitski, Alexei (2021), "Gauss-Lintel, an algorithm suite for exploring chord diagrams", in Kamareddine, Fairouz; Coen, Claudio Sacerdoti, Intelligent Computer Mathematics: 14th International Conference, CICM 2021, Timisoara, Romania, July 26-31, 2021, Proceedings, Lecture Notes in Computer Science, 12833, Berlin: Springer, pp. 197–202, doi:10.1007/978-3-030-81097-9_16
- ↑ A singular mathematical promenade, Lyon: ENS Éditions, 2017, ISBN 978-2-84788-939-0
 |