Intersection graph
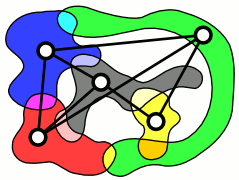
In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types of sets that are used to form an intersection representation of them.
Formal definition
Formally, an intersection graph G is an undirected graph formed from a family of sets
by creating one vertex vi for each set Si, and connecting two vertices vi and vj by an edge whenever the corresponding two sets have a nonempty intersection, that is,
All graphs are intersection graphs
Any undirected graph G may be represented as an intersection graph. For each vertex vi of G, form a set Si consisting of the edges incident to vi; then two such sets have a nonempty intersection if and only if the corresponding vertices share an edge. Therefore, G is the intersection graph of the sets Si.
(Erdős Goodman) provide a construction that is more efficient, in the sense that it requires a smaller total number of elements in all of the sets Si combined. For it, the total number of set elements is at most n2/4, where n is the number of vertices in the graph. They credit the observation that all graphs are intersection graphs to (Szpilrajn-Marczewski 1945), but say to see also (Čulík 1964). The intersection number of a graph is the minimum total number of elements in any intersection representation of the graph.
Classes of intersection graphs
Many important graph families can be described as intersection graphs of more restricted types of set families, for instance sets derived from some kind of geometric configuration:
- An interval graph is defined as the intersection graph of intervals on the real line, or of connected subgraphs of a path graph.
- An indifference graph may be defined as the intersection graph of unit intervals on the real line
- A circular arc graph is defined as the intersection graph of arcs on a circle.
- A polygon-circle graph is defined as the intersection of polygons with corners on a circle.
- One characterization of a chordal graph is as the intersection graph of connected subgraphs of a tree.
- A trapezoid graph is defined as the intersection graph of trapezoids formed from two parallel lines. They are a generalization of the notion of permutation graph, in turn they are a special case of the family of the complements of comparability graphs known as cocomparability graphs.
- A unit disk graph is defined as the intersection graph of unit disks in the plane.
- A circle graph is the intersection graph of a set of chords of a circle.
- The circle packing theorem states that planar graphs are exactly the intersection graphs of families of closed disks in the plane bounded by non-crossing circles.
- Scheinerman's conjecture (now a theorem) states that every planar graph can also be represented as an intersection graph of line segments in the plane. However, intersection graphs of line segments may be nonplanar as well, and recognizing intersection graphs of line segments is complete for the existential theory of the reals (Schaefer 2010).
- The line graph of a graph G is defined as the intersection graph of the edges of G, where we represent each edge as the set of its two endpoints.
- A string graph is the intersection graph of curves on a plane.
- A graph has boxicity k if it is the intersection graph of multidimensional boxes of dimension k, but not of any smaller dimension.
- A clique graph is the intersection graph of maximal cliques of another graph
- A block graph of clique tree is the intersection graph of biconnected components of another graph
(Scheinerman 1985) characterized the intersection classes of graphs, families of finite graphs that can be described as the intersection graphs of sets drawn from a given family of sets. It is necessary and sufficient that the family have the following properties:
- Every induced subgraph of a graph in the family must also be in the family.
- Every graph formed from a graph in the family by replacing a vertex by a clique must also belong to the family.
- There exists an infinite sequence of graphs in the family, each of which is an induced subgraph of the next graph in the sequence, with the property that every graph in the family is an induced subgraph of a graph in the sequence.
If the intersection graph representations have the additional requirement that different vertices must be represented by different sets, then the clique expansion property can be omitted.
Related concepts
An order-theoretic analog to the intersection graphs are the inclusion orders. In the same way that an intersection representation of a graph labels every vertex with a set so that vertices are adjacent if and only if their sets have nonempty intersection, so an inclusion representation f of a poset labels every element with a set so that for any x and y in the poset, x ≤ y if and only if f(x) ⊆ f(y).
See also
References
- Čulík, K. (1964), "Applications of graph theory to mathematical logic and linguistics", Theory of Graphs and its Applications (Proc. Sympos. Smolenice, 1963), Prague: Publ. House Czechoslovak Acad. Sci., pp. 13–20.
- "The representation of a graph by set intersections", Canadian Journal of Mathematics 18 (1): 106–112, 1966, doi:10.4153/CJM-1966-014-3, http://www.renyi.hu/~p_erdos/1966-21.pdf.
- Algorithmic Graph Theory and Perfect Graphs, Academic Press, 1980, ISBN 0-12-289260-7.
- McKee, Terry A.; McMorris, F. R. (1999), Topics in Intersection Graph Theory, SIAM Monographs on Discrete Mathematics and Applications, 2, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 0-89871-430-3.
- "Sur deux propriétés des classes d'ensembles", Fund. Math. 33: 303–307, 1945, doi:10.4064/fm-33-1-303-307.
- Schaefer, Marcus (2010), "Complexity of some geometric and topological problems", Graph Drawing, 17th International Symposium, GS 2009, Chicago, IL, USA, September 2009, Revised Papers, Lecture Notes in Computer Science, 5849, Springer-Verlag, pp. 334–344, doi:10.1007/978-3-642-11805-0_32, ISBN 978-3-642-11804-3, http://ovid.cs.depaul.edu/documents/convex.pdf.
- Scheinerman, Edward R. (1985), "Characterizing intersection classes of graphs", Discrete Mathematics 55 (2): 185–193, doi:10.1016/0012-365X(85)90047-0.
Further reading
- For an overview of both the theory of intersection graphs and important special classes of intersection graphs, see (McKee McMorris).
External links
- Jan Kratochvíl, A video lecture on intersection graphs (June 2007)
- E. Prisner, A Journey through Intersection Graph County
 |
