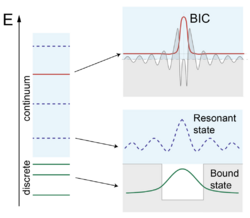
Bound state in the continuum
A bound state in the continuum (BIC) is an eigenstate of some particular quantum system with the following properties:
- Energy lies in the continuous spectrum of propagating modes of the surrounding space;
- The state does not interact with any of the states of the continuum (it cannot emit and cannot be excited by any wave that came from the infinity);
- Energy is real and Q factor is infinite, if there is no absorption in the system.
BICs are observed in electronic, photonic, acoustic systems. Bound states in the forbidden zone, where there are no finite solutions at infinity, are widely known (atoms, quantum dots, defects in semiconductors). For solutions in a continuum that are associated with this continuum, resonant states[1] are known, which decay (lose energy) over time. They can be excited, for example, by an incident wave with the same energy. The bound states in the continuum have real energy eigenvalues and therefore do not interact with the states of the continuous spectrum and cannot decay.[2]
Classification of bound states in the continuum by mechanism of occurrence
Source:[2]
BICs arising when solving the inverse problem
Wigner-von Neumann's BIC (Potential engineering)
The wave function of one of the continuum states is modified to be normalizable and the corresponding potential is selected for it.
| Examples |
|---|
|
In the work of von Neumann and Wigner [4] two types of spherically symmetric potentials are considered, with the potential of [math]\displaystyle{ V(r)=\frac{2}{r^2}-9r^4 }[/math] localization occurs due to the "reflection" from infinity (since the material point goes to infinity for a finite time, rolling down from this potential, and the probability of being there tends to zero). A similar example in 1D considers the exponential dependence of the potential.[5] The second type of potential[6][7] has a complex shape, but is periodically modulated with period [math]\displaystyle{ \pi }[/math]. A wave function with period [math]\displaystyle{ 2\pi }[/math] is reflected from such a potential to the center in analogy to the reflection from a Bragg mirror. In the one-dimensional case, such potentials can be realized using superlattices.[8][9] |
Hopping rate engineering
In the tight binding approximation, the jump rates are modified so that the state becomes localized
| Examples |
|---|
|
BICs of this type have been realized in an array of coupled optical waveguides,[10] with the hopping rate modulated by the spacing between the waveguides. Experimentally, a state with following rates
was realized in the system which consist of 40 waveguides. There are also examples of BICs in PT-symmetric systems.[11][12] |
Boundary shape engineering
Sources for BICs of different types, e.g. Fabry - Perot type are replaced by scatterers so as to create BIC of the same type.
| Examples |
|---|
|
BICs of this type are observed for water waves.[13][14][15][16] |
BICs arising due to parameter tuning
Fabry-Perot BICs
For resonant structures, the reflection coefficient near resonance can reach unity. Two such structures can be arranged in such a way that they radiate in antiphase and compensate each other.
| Examples |
|---|
|
In addition to the waves on water mentioned above, states of this type are found in many systems, such as those of pairs of quantum dots coupled to a waveguide,[17][18] double chains of copper atoms,[19] waveguide pairs of Z- and П- shapes [20] In photonics, states are realized, for example, in pairs of two-dimensional photonic crystal slabs,[21] double arrays of dielectric cylinders[22] etc.[23] |
Friedrich-Wintgen BICs
Two modes of the same symmetry of one and the same structure approach each other when the parameters of the structure are changed, and at some point an anti-crossing occurs. In this case, BIC is formed on one of the branches, since the modes as if compensate each other, being in antiphase and radiating into the same radiation channel.[24][25]
| Examples |
|---|
|
Friedrich-Wintgen BICs (FW BICs) were considered for a hydrogen atom in a magnetic field[26] and experimentally manifested in inhibition of autoionization of barium atom,[27] topological insulators with a defect [28] and many other quantum systmes.[29][30] Also, this type of BIC is found in two-dimensional and three-dimensional cylindrical open acoustic resonators.[31][32] In photonics, accidental BICs in periodic structures can sometimes appear as FW BICs,[33][34] also modes of this type appeared in Bragg waveguide at interaction of TE and TM waves through anisotropic medium.[35] A notable example is the theoretical realization of BIC on a layered spherical nanoparticle of specifically selected materials,[36][37] in this case BICs appear due to the interaction of different dipole modes of the same particle. By the same mechanism high-Q states can be realized in nonspherical dielectric resonators as well,[38][39] but in this case each mode consist of an infinite number of multipoles,[40] and the Q-factor doesn't go to infinity. |
Single-resonance parametric BICs
Occur when a single mode can be represented as a sum of contributions,[41] each of which varies with the structure parameters. At some point, destructive interference of all contributions occurs.
| Examples |
|---|
|
BICs of this type are usually considered in photonic crystals[42] and are also accidental BICs. They can appear in planar structures in [math]\displaystyle{ xy }[/math]-plane, which possess [math]\displaystyle{ {C_2}^z }[/math] and [math]\displaystyle{ \sigma_ z }[/math] symmetries,[43] but their existence is not guaranteed by symmetry, they appear for particular values of structure parameters. In addition to photonic periodic structures,[44][45] BICs of this type can appear for water waves,[46] quantum waveguides,[47] mechanical resonators,[48] as a surface waves[49] etc. |
Symmetry-protected BICs
Arise when the symmetry of the eigenstate differs from any of the possible symmetries of propagating modes in the continuum.
| Examples |
|---|
|
In the simple case, states of this type are observed in the Г-point of planar photonic crystals possessing symmetry [math]\displaystyle{ {C_n}^z }[/math].[50][51][52] Often, other types of BICs exist in the same structures. Also symmetry-protected BICs have been observed in coupled waveguide systems.[53][54] |
Separable BICs
Arise when the eigenvalue problem is solved by the Separation of Variables Method, and the wave function is represented, for example, as [math]\displaystyle{ \psi=\psi_1(x)\psi_2(y) }[/math], where both multipliers correspond to localized states, with the total energy lying in the continuum.
| Examples |
|---|
|
The Hamiltonian for obtaining this type of BIC was first proposed by Robnik[55] and then studied in various quantum systems[56][57] and 2D photonic structures.[58][59] |
Wigner-Von Neumann BICs
Bound states in the continuum were first predicted in 1929 by Eugene Wigner and John von Neumann.[4] Two potentials were described, in which BICs appear for two different reasons.
In this work, a spherically symmetric wave function is first chosen so as to be quadratically integrable over the entire space. Then a potential is chosen such that this wave function corresponds to zero energy.
The potential is spherically symmetric, then the wave equation will be written as follows:
- [math]\displaystyle{ -\frac{h^{2}}{8 \pi^{2} m} \Delta \psi+(V(r)-E) \psi=0, }[/math]
the angle derivatives disappear, since we limit ourselves to considering only spherically symmetric wave functions:
- [math]\displaystyle{ \Delta=\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}}=\frac{\partial^{2}}{\partial r^{2}}+\frac{2}{r} \frac{\partial}{\partial r}, }[/math]
For [math]\displaystyle{ E=0 }[/math] to be the eigenvalue for the spherically symmetric wave function [math]\displaystyle{ \psi=\psi(r) }[/math], the potential must be
- [math]\displaystyle{ V=\frac{h^{2}}{8 \pi^{2} m}\left(\frac{\psi^{\prime \prime}}{\psi}+\frac{2 \psi^{\prime}}{r \psi}\right) }[/math].
We obtain the specific values [math]\displaystyle{ \psi }[/math] and [math]\displaystyle{ V }[/math] for which the BIC will be observed.
First case
Let us consider the function [math]\displaystyle{ \psi=r^\alpha{\sin r^\beta} }[/math]. While the integral [math]\displaystyle{ \int_0^\infty 4\pi r^2|\psi(r)|^2\text{d}r=\int_0^\infty 4\pi r^{2\alpha+2}{\sin^2 r^\beta}\text{d}r }[/math] must be finite, then considering the behavior when [math]\displaystyle{ r=0 }[/math], we get that [math]\displaystyle{ 2\alpha+\beta+2\gt -1 }[/math], then considering the behavior when [math]\displaystyle{ r=\infty }[/math], we get [math]\displaystyle{ 2\alpha+2\lt -1 }[/math]. The regularity [math]\displaystyle{ V(r) }[/math] in [math]\displaystyle{ r\neq0 }[/math] requires [math]\displaystyle{ 2\alpha+\beta+1=0 }[/math]. Finally, we get [math]\displaystyle{ \alpha=-2, \ \beta=3 }[/math].
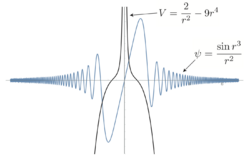
Assuming [math]\displaystyle{ \psi(r)=\frac{\sin r^3}{r^2} }[/math], then the potential will be equal to (discarding the irrelevant multiplier [math]\displaystyle{ {h^{2}}/{8 \pi^{2} m} }[/math]):
- [math]\displaystyle{ V(r)=\frac{2}{r^2}-9r^4 }[/math]
The eigenfunction and the potential curve are shown in the figure. It seems that the electron will simply roll off the potential and the energy will belong to the solid spectrum, but there is a stationary orbit with [math]\displaystyle{ E=0 }[/math].
In the work [4] is given the following interpretation: this behavior can be understood from an analogy with classical mechanics (considerations belong to Leo Szilard). The motion of a material point in the potential [math]\displaystyle{ V=\frac{2}{r^2}-9r^4 }[/math] is described by the following equation:
- [math]\displaystyle{ {\frac{m}{2}\left(\frac{\text{d} r}{\text{d} t}\right)^{2}+V(r)=\mathrm{Const}} }[/math]
- [math]\displaystyle{ {\frac{\text{d} r}{\text{d} t}=\sqrt{\frac{2}{m} \mathrm{Const}-\frac{4}{m} \frac{{1}}{r^{2}}+\frac{18}{m} r^{4}}} }[/math]
It's easy to see that when [math]\displaystyle{ r\rightarrow \infty }[/math], [math]\displaystyle{ \frac{\text{d}r}{\text{d}t}\rightarrow \infty }[/math], so the asymptotic is
- [math]\displaystyle{ \frac{d r}{d t}=\frac{3 \sqrt{2}}{\sqrt{m}} r^{2}; \ \ \ \ \ \ \ \frac{1}{r}=\frac{3 \sqrt{2}}{\sqrt{m}}\left(t_{0}-t\right) , \ \ }[/math] [math]\displaystyle{ r=\frac{\sqrt{m}}{3 \sqrt{2}\left(t_{0}-t\right)} }[/math]
that is, for a finite time [math]\displaystyle{ t=t_0 }[/math] the point goes to infinity. The stationary solution [math]\displaystyle{ \psi(r) }[/math] means that the point returns from infinity again, that it is as if it is reflected from there and starts oscillating. The fact that [math]\displaystyle{ \psi(r) }[/math] at [math]\displaystyle{ r=\infty }[/math] tends to zero follows from the fact that it rolls down a large potential slide and has an enormous speed and therefore a short lifetime. And since the whole oscillatory process (from [math]\displaystyle{ r_{min} }[/math] to infinity and back) is periodic, it is logical that this quantum mechanical problem has a stationary solution.
Second case
Let's move on to the second example, which can no longer be interpreted from such considerations.
First of all, we take a function [math]\displaystyle{ \psi=\frac{\sin r}{r} }[/math], then [math]\displaystyle{ V=-1 }[/math]. These are divergent spherical waves, since the energy [math]\displaystyle{ E=0 }[/math] is greater than the potential [math]\displaystyle{ V=-1 }[/math], the classical kinetic energy remains positive. The wave function belongs to a continuous spectrum, the integral [math]\displaystyle{ \int_0^\infty 4\pi r^2|\psi(r)|^2\text{d}r=4\pi \int_0^\infty \sin^2 r\text{d}r }[/math] diverges. Let's try to change the wave function so that the quadratic integral converges and the potential varies near -1.
Consider the following ansatz:
- [math]\displaystyle{ \psi=\frac{\sin r}{r}f(r) }[/math]
If the function [math]\displaystyle{ f(r) }[/math] is continuous, and at [math]\displaystyle{ r \rightarrow \infty }[/math] the asymptotic is [math]\displaystyle{ r^\alpha, \ \ \alpha\lt -1/2 }[/math] then the integral is finite. The potential would then be equal (with the corrected arithmetical error in the original article):[7]
- [math]\displaystyle{ V=-1+2 \operatorname{ctg} r \frac{f^{\prime}(r)}{f(r)}+\frac{f^{\prime \prime}(r)}{f(r)}. }[/math]
In order for the potential to remain near -1, and at [math]\displaystyle{ r\rightarrow \infty }[/math] tend to -1, we must make the functions [math]\displaystyle{ \operatorname{ctg} r \frac{f^{\prime}(r)}{f(r)}, \ \frac{f^{\prime \prime}(r)}{f(r)} }[/math] small and at [math]\displaystyle{ r\rightarrow \infty }[/math] tend to zero.
In the first case, also [math]\displaystyle{ \frac{f^{\prime}(r)}{f(r)} }[/math] should vanish for [math]\displaystyle{ \operatorname{ctg} r= \infty }[/math], namely for [math]\displaystyle{ r=0,\pi, \ 2\pi, \ 2\pi, \dots }[/math], that is for [math]\displaystyle{ \sin r=0 }[/math]. This is the case when [math]\displaystyle{ f(r)=\int_0^r \sin^2r \text{d}r=\frac{r}2-\frac14\sin2r }[/math] or any other function of this expression.
Let assume [math]\displaystyle{ f(r)=[A^2+(\frac{r}2-\frac14\sin2r)^2]^{-1} }[/math], where [math]\displaystyle{ A }[/math] is arbitrary (here [math]\displaystyle{ f(r) }[/math] tends to [math]\displaystyle{ r^\alpha, \ \ \alpha\lt -1/2 }[/math] when [math]\displaystyle{ r\rightarrow \infty }[/math]). Then
- [math]\displaystyle{ \psi=\frac{\sin r}{r(A^2+(2r-\sin2r)^2)}. }[/math]
The expression for the potential is cumbersome, but the graphs show that for [math]\displaystyle{ r\rightarrow \infty }[/math] the potential tends to -1. Furthermore, it turns out that for any [math]\displaystyle{ \varepsilon\gt 0 }[/math] one can choose such an A that the potential is between [math]\displaystyle{ -1-\varepsilon }[/math] and [math]\displaystyle{ -1+\varepsilon }[/math]. We can see that the potential oscillates with period [math]\displaystyle{ \pi }[/math] and the wave function oscillates with period [math]\displaystyle{ 2\pi }[/math]. It turns out that all reflected waves from the "humps" of such a potential are in phase, and the function is localized in the center, being reflected from the potential by a mechanism similar to the reflection from a Bragg mirror.
Notes
- ↑ Technically, bound states belong to the pure point spectrum, not the discrete spectrum. See Decomposition of spectrum (functional analysis) and "Simon, B. (1978). "An Overview of Rigorous Scattering Theory". p. 3."
- ↑ 1.0 1.1 Maheswari, A. Uma; Prema, P.; Shastry, C. S. (2010). "Resonant states and transmission coefficient oscillations for potential wells and barriers". American Journal of Physics 78 (4): 412–417. doi:10.1119/1.3276053. Bibcode: 2010AmJPh..78..412M.
- ↑ 2.0 2.1 2.2 Hsu, Chia Wei; Zhen, Bo; Stone, A. Douglas; Joannopoulos, John D.; Soljačić, Marin (2016). "Bound states in the continuum". Nature Reviews Materials 1 (9): 16048. doi:10.1038/natrevmats.2016.48. Bibcode: 2016NatRM...116048H.
- ↑ Koshelev, K .; Bogdanov, A .; Kivshar, Y. Engineering with bound states in the continuum. Opt. Photonics News 2020, 31, 38−45
- ↑ 4.0 4.1 4.2 J. von Neumann, E.P. Wigner (1929). "Über merkwürdige diskrete Eigenwerte". Phys. Z. 30: 465–467.
- ↑ Zafar Ahmed et al 2019 Phys. Scr. 94 105214
- ↑ Simon, B. On positive eigenvalues of one-body Schrödinger operators. Commun. Pure Appl. Math. 22, 531-538 (1969)
- ↑ 7.0 7.1 Stillinger, F. H. & Herrick, D. R. Bound states in the continuum. Phys. Rev. A 11, 446-454 (1975)
- ↑ D. R. Herrick, "Construction of bound states in the continuum for epitaxial heterostructure superlattices," Physica B 85, 44-50 (1977).
- ↑ Molina, M. I., Miroshnichenko, A. E. & Kivshar, Y. S. Surface bound states in the continuum. Phys. Rev. Lett. 108, 070401 (2012)
- ↑ Corrielli, G., Della Valle, G., Crespi, A., Osellame, R. & Longhi, S. Observation of surface states with algebraic localization. Phys. Rev. Lett. 111, 220403 (2013)
- ↑ Stefano Longhi. Non-Hermitian tight-binding network engineering. Phys. Rev. A 93, 022102
- ↑ Stefano Longhi, "Bound states in the continuum in PT-symmetric optical lattices, " Opt. Lett. 39, 1697—1700 (2014)
- ↑ McIver, M. An example of non-uniqueness in the two-dimensional linear water wave problem. J. Fluid Mech. 315, 257—266 (1996)
- ↑ Kuznetsov, N. & McIver, P. On uniqueness and trapped modes in the water-wave problem for a surface-piercing axisymmetric body. Q. J. Mech. Appl. Math. 50, 565—580 (1997)
- ↑ Porter, R. & Evans, D. V. Water-wave trapping by floating circular cylinders. J. Fluid Mech. 633, 311—325 (2009).
- ↑ Cobelli, P. J.; Pagneux, V.; Maurel, A.; Petitjeans, P. (2011). "Experimental study on water-wave trapped modes". Journal of Fluid Mechanics 666: 445–476. doi:10.1017/S0022112010004222. Bibcode: 2011JFM...666..445C. https://hal.science/hal-03994541/file/art_59.pdf.
- ↑ Cattapan, G. & Lotti, P. Bound states in the continuum in two-dimensional serial structures. Eur. Phys. J. B 66, 517–523 (2008)
- ↑ Sadreev, A. F., Bulgakov, E. N. & Rotter, I. Trapping of an electron in the transmission through two quantum dots coupled by a wire. JETP Lett. 82, 498–503 (2005)
- ↑ Díaz-Tendero, S., Borisov, A. G. & Gauyacq, J.-P. Extraordinary electron propagation length in a metallic double chain supported on a metal surface. Phys. Rev. Lett. 102, 166807 (2009)
- ↑ Sadreev, A. F., Maksimov, D. N. & Pilipchuk, A. S. Gate controlled resonant widths in double-bend waveguides: bound states in the continuum. J. Phys. Condens. Matter 27, 295303 (2015).
- ↑ Suh, W., Yanik, M. F., Solgaard, O. & Fan, S. Displacement-sensitive photonic crystal structures based on guided resonance in photonic crystal slabs. Appl. Phys. Lett. 82, 1999—2001 (2003)
- ↑ Ndangali, R. F. & Shabanov, S. V. Electromagnetic bound states in the radiation continuum for periodic double arrays of subwavelength dielectric cylinders. J. Math. Phys. 51, 102901 (2010)
- ↑ Chernyak, A. M.; Barsukova, M. G.; Shorokhov, A. S.; Musorin, A. I.; Fedyanin, A. A. (2020). "Bound States in the Continuum in Magnetophotonic Metasurfaces". JETP Letters 111 (1): 46–49. doi:10.1134/S0021364020010105. Bibcode: 2020JETPL.111...46C.
- ↑ Friedrich, H. & Wintgen, D. Interfering resonances and bound states in the continuum. Phys. Rev. A 32, 3231-3242 (1985)
- ↑ Remacle, F.; Munster, M.; Pavlov-Verevkin, V.B.; Desouter-Lecomte, M. (1990). "Trapping in competitive decay of degenerate states". Physics Letters A 145 (5): 265–268. doi:10.1016/0375-9601(90)90361-q. Bibcode: 1990PhLA..145..265R.
- ↑ Friedrich, H. & Wintgen, D. Physical realization of bound states in the continuum. Phys. Rev. A 31, 3964-3966 (1985)
- ↑ Neukammer, J.; Rinneberg, H.; Jönsson, G.; Cooke, W. E.; Hieronymus, H.; König, A.; Vietzke, K.; Spinger-Bolk, H. (1985). "Autoionization Inhibited by Internal Interferences". Physical Review Letters 55 (19): 1979–1982. doi:10.1103/physrevlett.55.1979. PMID 10031978. Bibcode: 1985PhRvL..55.1979N. https://lup.lub.lu.se/record/2259032.
- ↑ Sablikov, V. A. & Sukhanov, A. A. Helical bound states in the continuum of the edge states in two dimensional topological insulators. Phys. Lett. A 379, 1775—1779 (2015)
- ↑ Sadreev, A. F., Bulgakov, E. N. & Rotter, I. Bound states in the continuum in open quantum billiards with a variable shape. Phys. Rev. B 73, 235342 (2006)
- ↑ Texier, C. Scattering theory on graphs: II. The Friedel sum rule. J. Phys. A 35, 3389 (2002).
- ↑ Hein, S., Koch, W. & Nannen, L. Trapped modes and Fano resonances in two-dimensional acoustical duct-cavity systems. J. Fluid Mech. 692, 257—287 (2012)
- ↑ Lyapina, A. A., Maksimov, D. N., Pilipchuk, A. S. & Sadreev, A. F. Bound states in the continuum in open acoustic resonators. J. Fluid Mech. 780, 370—387 (2015)
- ↑ Bulgakov, Evgeny N.; Maksimov, Dmitrii N. (2018). "Avoided crossings and bound states in the continuum in low-contrast dielectric gratings". Physical Review A 98 (5): 053840. doi:10.1103/physreva.98.053840. Bibcode: 2018PhRvA..98e3840B.
- ↑ Lee, Sun-Goo; Kim, Seong-Han; Kee, Chul-Sik (2020). "Bound states in the continuum (BIC) accompanied by avoided crossings in leaky-mode photonic lattices". Nanophotonics 9 (14): 4373–4380. doi:10.1515/nanoph-2020-0346. Bibcode: 2020Nanop...9..346L.
- ↑ Pankin, P. S.; Wu, B.-R.; Yang, J.-H.; Chen, K.-P.; Timofeev, I. V.; Sadreev, A. F. (2020). "One-dimensional photonic bound states in the continuum". Communications Physics 3 (1): 91. doi:10.1038/s42005-020-0353-z. Bibcode: 2020CmPhy...3...91P.
- ↑ Embedded Photonic Eigenvalues in 3D Nanostructures. Francesco Monticone and Andrea Alù. Phys. Rev. Lett. 112, 213903 (2014)
- ↑ M. G. Silveirinha, Phys. Rev. A 89, 023813 (2014).
- ↑ Rybin, Mikhail V.; Koshelev, Kirill L.; Sadrieva, Zarina F.; Samusev, Kirill B.; Bogdanov, Andrey A.; Limonov, Mikhail F.; Kivshar, Yuri S. (2017). "High- [math]\displaystyle{ Q }[/math] Supercavity Modes in Subwavelength Dielectric Resonators". Physical Review Letters 119 (24): 243901. doi:10.1103/physrevlett.119.243901. PMID 29286713.
- ↑ K. Koshelev et al., Science 367, 288—292 (2020).
- ↑ S. Gladyshev, K. Frizyuk, A. Bogdanov Phys. Rev. B 102, 075103 — Published 3 August 2020
- ↑ Gao, Xingwei; Hsu, Chia Wei; Zhen, Bo; Lin, Xiao; Joannopoulos, John D.; Soljačić, Marin; Chen, Hongsheng (2016). "Formation mechanism of guided resonances and bound states in the continuum in photonic crystal slabs". Scientific Reports 6: 31908. doi:10.1038/srep31908. PMID 27557882. Bibcode: 2016NatSR...631908G.
- ↑ Hsu, C. W. et al. Observation of trapped light within the radiation continuum. Nature 499, 188—191 (2013)
- ↑ B. Zhen, C. W. Hsu, L. Lu, A. D. Stone, and M. Soljaˇci ́c, "Topological Nature of Optical Bound States in the Continuum, " Phys. Rev. Lett. 113, 257401 (2014)
- ↑ Porter, R. & Evans, D. V. Embedded Rayleigh-Bloch surface waves along periodic rectangular arrays. Wave Motion 43, 29-50 (2005).
- ↑ Bulgakov, E. N. & Sadreev, A. F. Light trapping above the light cone in a one-dimensional array of dielectric spheres. Phys. Rev. A 92, 023816 (2015)
- ↑ McIver, M., Linton, C. M., McIver, P., Zhang, J. & Porter, R. Embedded trapped modes for obstacles in two-dimensional waveguides. Q. J. Mech. Appl. Math. 54, 273—293 (2001).
- ↑ Linton, C. M. & Ratcliffe, K. Bound states in coupled guides. I. Two dimensions. J. Math. Phys. 45, 1359—1379 (2004).
- ↑ Chen, Y. et al. Mechanical bound state in the continuum for optomechanical microresonators. New J. Phys. 18, 063031 (2016)
- ↑ Yamanouchi, K. & Shibayama, K. Propagation and amplification of rayleigh waves and piezoelectric leaky surface waves in LiNbO3 . J. Appl. Phys. 43, 856—862 (1972).
- ↑ B. Zhen, C. W. Hsu, L. Lu, A. D. Stone, and M. Soljaˇci ́c, "Topological Nature of Optical Bound States in the Continuum, " Phys. Rev. Lett. 113, 257401 (2014).
- ↑ Z. Sadrieva, K. Frizyuk, M. Petrov, Yu. Kivshar, and A.Bogdanov «Multipolar origin of bound states in the continuum» Phys. Rev. B 100, 115303
- ↑ Lee, J. et al. Observation and differentiation of unique high-Q optical resonances near zero wave vector in macroscopic photonic crystal slabs. Phys. Rev. Lett. 109, 067401 (2012)
- ↑ Dreisow, F. et al. Adiabatic transfer of light via a continuum in optical waveguides. Opt. Lett. 34, 2405—2407 (2009)
- ↑ Plotnik, Y. et al. Experimental observation of optical bound states in the continuum. Phys. Rev. Lett. 107, 183901 (2011).
- ↑ Robnik, M. A simple separable Hamiltonian having bound states in the continuum. J. Phys. A 19, 3845 (1986).
- ↑ Duclos, P., Exner, P. & Meller, B. Open quantum dots: resonances from perturbed symmetry and bound states in strong magnetic fields. Rep. Math. Phys. 47, 253—267 (2001).
- ↑ Prodanovic´, N., Milanovic´, V., Ikonic´, Z., Indjin, D. & Harrison, P. Bound states in continuum: quantum dots in a quantum well. Phys. Lett. A 377, 2177—2181 (2013).
- ↑ Čtyroký, J. Photonic bandgap structures in planar waveguides. J. Opt. Soc. Am. A 18, 435—441 (2001).
- ↑ Watts, M. R., Johnson, S. G., Haus, H. A. & Joannopoulos, J. D. Electromagnetic cavity with arbitrary Q and small modal volume without a complete photonic bandgap. Opt. Lett. 27, 1785—1787 (2002).
Literature
- Hsu, Chia Wei; Zhen, Bo; Stone, A. Douglas; Joannopoulos, John D.; Soljačić, Marin (2016). "Bound states in the continuum". Nature Reviews Materials 1 (9). doi:10.1038/natrevmats.2016.48. Bibcode: 2016NatRM...116048H.
- Koshelev, Kirill; Bogdanov, Andrey; Kivshar, Yuri (2020). "Engineering with Bound States in the Continuum". Optics and Photonics News 31 (1): 38. doi:10.1364/OPN.31.1.000038. Bibcode: 2020OptPN..31a..38K.
- Azzam, Shaimaa I.; Kildishev, Alexander V. (2021). "Photonic Bound States in the Continuum: From Basics to Applications". Advanced Optical Materials 9. doi:10.1002/adom.202001469.
- Sadreev, Almas F. (2021). "Interference traps waves in an open system: Bound states in the continuum". Reports on Progress in Physics 84 (5). doi:10.1088/1361-6633/abefb9. PMID 33730696. Bibcode: 2021RPPh...84e5901S.
 |