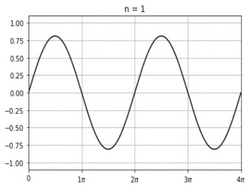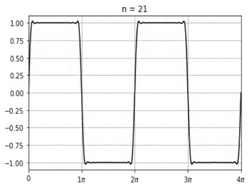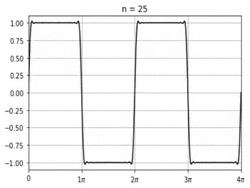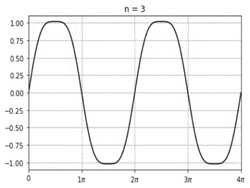
Sigma approximation
In mathematics, σ-approximation adjusts a Fourier summation to greatly reduce the Gibbs phenomenon, which would otherwise occur at discontinuities.[1][2]
A σ-approximated summation for a series of period T can be written as follows: [math]\displaystyle{ s(\theta) = \frac{1}{2} a_0 + \sum_{k=1}^{m-1} \operatorname{sinc} \frac{k}{m} \cdot \left[a_{k} \cos \left( \frac{2 \pi k}{T} \theta \right) + b_k \sin \left( \frac{2 \pi k}{T} \theta \right) \right], }[/math] in terms of the normalized sinc function [math]\displaystyle{ \operatorname{sinc} x = \frac{\sin \pi x}{\pi x}. }[/math]
The term [math]\displaystyle{ \operatorname{sinc} \frac{k}{m} }[/math] is the Lanczos σ factor, which is responsible for eliminating most of the Gibbs phenomenon. It does not do so entirely, however, but one can square or even cube the expression to serially attenuate Gibbs phenomenon in the most extreme cases.
See also
References
- ↑ Chhoa, Jannatul Ferdous (2020-08-01). "An Adaptive Approach to Gibbs' Phenomenon". Master's Theses. https://aquila.usm.edu/masters_theses/762.
- ↑ Recktenwald, Steffen M.; Wagner, Christian; John, Thomas (2021-06-29). "Optimizing pressure-driven pulsatile flows in microfluidic devices" (in en). Lab on a Chip 21 (13): 2605–2613. doi:10.1039/D0LC01297A. ISSN 1473-0189. PMID 34008605.
 |