Process performance index
This article's factual accuracy is disputed. (February 2021) (Learn how and when to remove this template message) |
In process improvement efforts, the process performance index is an estimate of the process capability of a process during its initial set-up, before it has been brought into a state of statistical control.[1]
Formally, if the upper and lower specifications of the process are USL and LSL, the estimated mean of the process is [math]\displaystyle{ \hat{\mu} }[/math], and the estimated variability of the process (expressed as a standard deviation) is [math]\displaystyle{ \hat{\sigma} }[/math], then the process performance index is defined as:
- [math]\displaystyle{ \hat{P}_{pk} = \min \Bigg[ {USL - \hat{\mu} \over 3 \hat{\sigma}}, { \hat{\mu} - LSL \over 3 \hat{\sigma}} \Bigg] }[/math]
[math]\displaystyle{ \hat{\sigma} }[/math] is estimated using the sample standard deviation. Ppk may be negative if the process mean falls outside the specification limits (because the process is producing a large proportion of defective output).
Some specifications may only be one sided (for example, strength). For specifications that only have a lower limit, [math]\displaystyle{ \hat{P}_{p,lower} = {\hat{\mu} - LSL \over 3 \hat{\sigma}} }[/math]; for those that only have an upper limit, [math]\displaystyle{ \hat{P}_{p,upper} = {USL - \hat{\mu} \over 3 \hat{\sigma}} }[/math].
Practitioners may also encounter [math]\displaystyle{ \hat{P}_{p} = \frac{USL - LSL} {6 \hat{\sigma}} }[/math], a metric that does not account for process performance not exactly centered between the specification limits, and therefore is interpreted as what the process would be capable of achieving if it could be centered and stabilized.
Interpretation
Larger values of Ppk may be interpreted to indicate that a process is more capable of producing output within the specification limits, though this interpretation is controversial.[citation needed] Strictly speaking, from a statistical standpoint, Ppk is meaningless if the process under study is not in control because one cannot reliably estimate the process underlying probability distribution, let alone parameters like [math]\displaystyle{ \hat{\mu} }[/math] and [math]\displaystyle{ \hat{\sigma} }[/math].[2][disputed ] Furthermore, using this metric of past process performance to predict future performance is highly suspect.[3][disputed ]
From a management standpoint, when an organization is under pressure to set up a new process quickly and economically, Ppk is a convenient metric to gauge how set-up is progressing (increasing Ppk being interpreted as "the process capability is improving"). The risk is that Ppk is taken to mean a process is ready for production before all the kinks have been worked out of it.
Once a process is put into a state of statistical control, process capability is described using process capability indices, which are formulaically identical to Ppk (and Pp).[disputed ] The indices are named differently in order to call attention to whether the process under study is believed to be in control or not.
Example
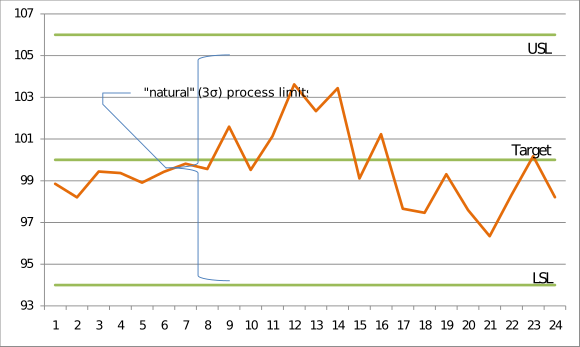
Consider a quality characteristic with a target of 100.00 μm and upper and lower specification limits of 106.00 μm and 94.00 μm, respectively. If, after carefully monitoring the process for a while, it appears that the process is out of control and producing output unpredictably (as depicted in the run chart below), one can't meaningfully estimate its mean and standard deviation. In the example below, the process mean appears to drift upward, settle for a while, and then drift downward.
If [math]\displaystyle{ \hat{\mu} }[/math] and [math]\displaystyle{ \hat{\sigma} }[/math] are estimated to be 99.61 μm and 1.84 μm, respectively, then
| Index |
|---|
| [math]\displaystyle{ \hat{P}_p = \frac{USL - LSL} {6 \hat{\sigma}} = \frac{106.00 - 94.00} {6 \times 1.84} = 1.09 }[/math] |
| [math]\displaystyle{ \hat{P}_{pk} = \min \Bigg[ {USL - \hat{\mu} \over 3 \hat{\sigma}}, { \hat{\mu} - LSL \over 3 \hat{\sigma}} \Bigg] = \min \Bigg[ {106.00 - 99.61 \over 3 \times 1.84}, { 99.61 - 94 \over 3 \times 1.84} \Bigg] = 1.02 }[/math] |
That the process mean appears to be unstable is reflected in the relatively low values for Pp and Ppk. The process is producing a significant number of defectives, and, until the cause of the unstable process mean is identified and eliminated, one really can't meaningfully quantify how this process will perform.
See also
References
- ↑ Montgomery, Douglas (2005), Introduction to Statistical Quality Control, Hoboken, New Jersey: John Wiley & Sons, pp. 348–349, ISBN 978-0-471-65631-9, OCLC 56729567, archived from the original on 2008-06-20, https://web.archive.org/web/20080620095346/http://www.eas.asu.edu/~masmlab/montgomery/
- ↑ Montgomery, Douglas (2005), Introduction to Statistical Quality Control, Hoboken, New Jersey: John Wiley & Sons, p. 349, ISBN 978-0-471-65631-9, OCLC 56729567, archived from the original on 2008-06-20, https://web.archive.org/web/20080620095346/http://www.eas.asu.edu/~masmlab/montgomery/, "However, please note that if the process is not in control, the indices Pp and Ppk have no meaningful interpretation relative to process capability, because they cannot predict process performance."
- ↑ Montgomery, Douglas (2005), Introduction to Statistical Quality Control, Hoboken, New Jersey: John Wiley & Sons, p. 349, ISBN 978-0-471-65631-9, OCLC 56729567, archived from the original on 2008-06-20, https://web.archive.org/web/20080620095346/http://www.eas.asu.edu/~masmlab/montgomery/, "Unless the process is stable (in control), no index is going to carry useful predictive information about process capability or convey any information about future performance."
 |