Soddy circles of a triangle
In geometry, the Soddy circles of a triangle are two circles associated with any triangle in the plane. Their centers are the Soddy centers of the triangle. They are all named for Frederick Soddy, who rediscovered Descartes' theorem on the radii of mutually tangent quadruples of circles.
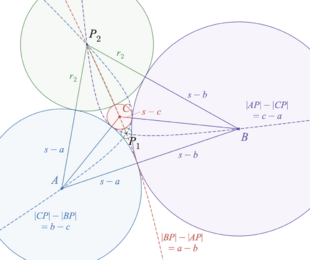
Any triangle has three externally tangent circles centered at its vertices. Two more circles, its Soddy circles, are tangent to the three circles centered at the vertices; their centers are called Soddy centers. The line through the Soddy centers is the Soddy line of the triangle. These circles are related to many other notable features of the triangle. They can be generalized to additional triples of tangent circles centered at the vertices in which one circle surrounds the other two.
Construction
Let [math]\displaystyle{ A, B, C }[/math] be the three vertices of a triangle, and let [math]\displaystyle{ a, b, c }[/math] be the lengths of the opposite sides, and [math]\displaystyle{ s = \tfrac12(a + b + c) }[/math] be the semiperimeter. Then the three Soddy circles centered at [math]\displaystyle{ A, B, C }[/math] have radii [math]\displaystyle{ s-a, s-b, s-c }[/math], respectively. By Descartes' theorem, two more circles, sometimes also called Soddy circles, are tangent to these three circles. The centers of these two tangent circles are the Soddy centers of the triangle.
Related features
Each of the three circles centered at the vertices crosses two sides of the triangle at right angles, at one of the three intouch points of the triangle, where its incircle is tangent to the side. The two circles tangent to these three circles are separated by the incircle, one interior to it and one exterior. The Soddy centers lie at the common intersections of three hyperbolas, each having two triangle vertices as foci and passing through the third vertex.[1][2][3]
The inner Soddy center is an equal detour point: the polyline connecting any two triangle vertices through the inner Soddy point is longer than the line segment connecting those vertices directly, by an amount that does not depend on which two vertices are chosen.[4] By Descartes' theorem, the inner Soddy circle's curvature is [math]\displaystyle{ (4R + r + 2s) / \Delta }[/math], where [math]\displaystyle{ \Delta }[/math] is the triangle's area, [math]\displaystyle{ R }[/math] is its circumradius, and [math]\displaystyle{ r }[/math] is its inradius. The outer Soddy circle has curvature [math]\displaystyle{ (4R + r - 2s) / \Delta }[/math].[5] When this curvature is positive, the outer Soddy center is another equal detour point; otherwise the equal detour point is unique.[4] When the outer Soddy circle has negative curvature, its center is the isoperimetric point of the triangle: the three triangles formed by this center and two vertices of the starting triangle all have the same perimeter.[4] Triangles whose outer Soddy circle degenerates to a straight line with curvature zero have been called "Soddyian triangles".[5] This happens when [math]\displaystyle{ 4R + r = 2s }[/math] and causes the curvature of the inner Soddy circle to be [math]\displaystyle{ 4/r }[/math].
Excentric circles
As well as the three externally tangent circles formed from a triangle, three more triples of tangent circles also have their centers at the triangle vertices, but with one of the circles surrounding the other two. Their triples of radii are [math]\displaystyle{ (-s, s-c, s-b), }[/math] [math]\displaystyle{ (s-c, -s, s-a), }[/math] or [math]\displaystyle{ (s-b, s-a, -s), }[/math] where a negative radius indicates that the circle is tangent to the other two in its interior. Their points of tangency lie on the lines through the sides of the triangle, with each triple of circles having tangencies at the points where one of the three excircles is tangent to these lines. The pairs of tangent circles to these three triples of circles behave in analogous ways to the pair of inner and outer circles, and are also sometimes called Soddy circles.[6] Instead of lying on the intersection of the three hyperbolas, the centers of these circles lie where the opposite branch of one hyperbola with foci at the two vertices and passing through the third intersects the two ellipses with foci at other pairs of vertices and passing through the third.[1]
Soddy lines
The line through both Soddy centers, called the Soddy line, also passes through the incenter of the triangle, which is the homothetic center of the two Soddy circles,[6] and through the Gergonne point, the intersection of the three lines connecting the intouch points of the triangle to the opposite vertices.[7] Four mutually tangent circles define six points of tangency, which can be grouped in three pairs of tangent points, each pair coming from two disjoint pairs of circles. The three lines through these three pairs of tangent points are concurrent, and the points of concurrency defined in this way from the inner and outer circles define two more triangle centers called the Eppstein points that also lie on the Soddy line.[7][8]
The three additional pairs of excentric Soddy circles each are associated with a Soddy line through their centers. Each passes through the corresponding excenter of the triangle, which is the center of similitude for the two circles. Each Soddy line also passes through an analog of the Gergonne point and the Eppstein points. The four Soddy lines concur at the de Longchamps point, the reflection of the orthocenter of the triangle about the circumcenter.[6][7][9]
References
- ↑ 1.0 1.1 "Compte rendu de la 19me session de l'association française pour l'avancement des sciences, pt. 2" (in fr). Congrès de Limoges 1890. Paris: Secrétariat de l'association. 1891. Template:Pgs, especially §4 "Sur les intersections deux a deux des coniques qui ont pour foyers-deux sommets d'un triangle et passent par le troisième" [On the intersections in pairs of the conics which have as foci two vertices of a triangle and pass through the third], Template:Pgs.
- ↑ Veldkamp, G. R. (1985), "The Isoperimetric Point and the Point(s) of Equal Detour in a Triangle", The American Mathematical Monthly 92 (8): 546–558, doi:10.1080/00029890.1985.11971677
- ↑ Garcia, Ronaldo; Reznik, Dan; Moses, Peter; Gheorghe, Liliana (2022), "Triads of conics associated with a triangle", KoG (Croatian Society for Geometry and Graphics) (26): 16–32, doi:10.31896/k.26.2, https://hrcak.srce.hr/file/417127
- ↑ 4.0 4.1 4.2 Hajja, Mowaffaq; Yff, Peter (2007), "The isoperimetric point and the point(s) of equal detour in a triangle", Journal of Geometry 87 (1–2): 76–82, doi:10.1007/s00022-007-1906-y, https://www.researchgate.net/publication/225560690
- ↑ 5.0 5.1 Jackson, Frank M. (2013), "Soddyian Triangles", Forum Geometricorum 13: 1–6, https://forumgeom.fau.edu/FG2013volume13/FG201301.pdf
- ↑ 6.0 6.1 6.2 Vandeghen, A. (1964), "Soddy's circles and the De Longchamps point of a triangle", The American Mathematical Monthly 71 (2): 176–179, doi:10.2307/2311750
- ↑ 7.0 7.1 7.2 Gisch, David; Ribando, Jason M. (2004), "Apollonius' problem: a study of solutions and their connections", American Journal of Undergraduate Research 3 (1), doi:10.33697/ajur.2004.010, https://www.ajuronline.org/uploads/Volume%203/Issue%201/31D-GischArt.pdf
- ↑ Eppstein, David (2001), "Tangent spheres and triangle centers", The American Mathematical Monthly 108 (1): 63–66, doi:10.1080/00029890.2001.11919724
- ↑ "A fourfold point of concurrence lying on the Euler line of a triangle", The Mathematical Intelligencer 22 (1): 54–59, 2000, doi:10.1007/bf03024448
External links
- Bogomolny, Alexander, "Soddy circles and David Eppstein's centers", Cut-the-knot, http://www.cut-the-knot.org/Curriculum/Geometry/Eppstein.shtml
 |