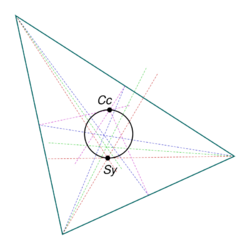
Brocard circle
In geometry, the Brocard circle (or seven-point circle) for a triangle is a circle defined from a given triangle. It passes through the circumcenter and symmedian of the triangle, and is centered at the midpoint of the line segment joining them (so that this segment is a diameter).
Equation
In terms of the side lengths [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math], and [math]\displaystyle{ c }[/math] of the given triangle, and the areal coordinates [math]\displaystyle{ (x,y,z) }[/math] for points inside the triangle (where the [math]\displaystyle{ x }[/math]-coordinate of a point is the area of the triangle made by that point with the side of length [math]\displaystyle{ a }[/math], etc), the Brocard circle consists of the points satisfying the equation[1]
- [math]\displaystyle{ a^2yz+b^2zx+c^2xy=\frac{a^2b^2c^2(x+y+z)}{a^2+b^2+c^2}\left(\frac{x}{a^2}+\frac{y}{b^2}+\frac{z}{c^2}\right). }[/math]
Related points
The two Brocard points lie on this circle, as do the vertices of the Brocard triangle.[2] These five points, together with the other two points on the circle (the circumcenter and symmedian), justify the name "seven-point circle".
The Brocard circle is concentric with the first Lemoine circle.[3]
Special cases
If the triangle is equilateral, the circumcenter and symmedian coincide and therefore the Brocard circle reduces to a single point.[4]
History
The Brocard circle is named for Henri Brocard,[5] who presented a paper on it to the French Association for the Advancement of Science in Algiers in 1881.[6]
References
- ↑ Moses, Peter J. C. (2005), "Circles and triangle centers associated with the Lucas circles", Forum Geometricorum 5: 97–106, https://forumgeom.fau.edu/FG2005volume5/FG200513.pdf, retrieved 2019-01-05
- ↑ A history of elementary mathematics: with hints on methods of teaching, The Macmillan company, 1917, p. 261, https://books.google.com/books?id=vgYCAAAAYAAJ&pg=PA261.
- ↑ Episodes in Nineteenth and Twentieth Century Euclidean Geometry, New Mathematical Library, 37, Cambridge University Press, 1995, p. 110, ISBN 9780883856390, https://books.google.com/books?id=6oduPgvOAhwC&pg=PA110.
- ↑ Smart, James R. (1997), Modern Geometries (5th ed.), Brooks/Cole, p. 184, ISBN 0-534-35188-3
- ↑ Guggenbuhl, Laura (1953), "Henri Brocard and the geometry of the triangle", The Mathematical Gazette 37 (322): 241–243.
- ↑ O'Connor, John J.; Robertson, Edmund F., "Henri Brocard", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Brocard.html.
External links
See also