Ramanujan–Soldner constant

Ramanujan–Soldner constant as seen on the logarithmic integral function.

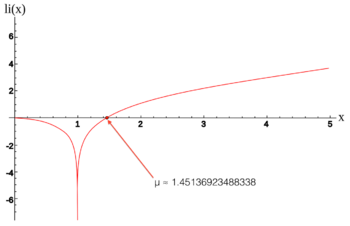
In mathematics, the Ramanujan–Soldner constant (also called the Soldner constant) is a mathematical constant defined as the unique positive zero of the logarithmic integral function. It is named after Srinivasa Ramanujan and Johann Georg von Soldner.

Its value is approximately μ ≈ 1.45136923488338105028396848589202744949303228… (sequence A070769 in the OEIS)

Since the logarithmic integral is defined by

[math]\displaystyle{ \mathrm{li}(x) = \int_0^x \frac{dt}{\ln t}, }[/math]

then using [math]\displaystyle{ \mathrm{li}(\mu) = 0, }[/math] we have

[math]\displaystyle{ \mathrm{li}(x)\;=\;\mathrm{li}(x) - \mathrm{li}(\mu) = \int_0^x \frac{dt}{\ln t} - \int_0^{\mu} \frac{dt}{\ln t} = \int_{\mu}^x \frac{dt}{\ln t}, }[/math]

thus easing calculation for numbers greater than μ. Also, since the exponential integral function satisfies the equation

[math]\displaystyle{ \mathrm{li}(x)\;=\;\mathrm{Ei}(\ln{x}), }[/math]

the only positive zero of the exponential integral occurs at the natural logarithm of the Ramanujan–Soldner constant, whose value is approximately ln(μ) ≈ 0.372507410781366634461991866… (sequence A091723 in the OEIS)

External links

• Weisstein, Eric W.. "Soldner's Constant". http://mathworld.wolfram.com/SoldnersConstant.html.