Maxwell's theorem (geometry)

Short description: Given a triangle and a point, constructs a second triangle with a special point

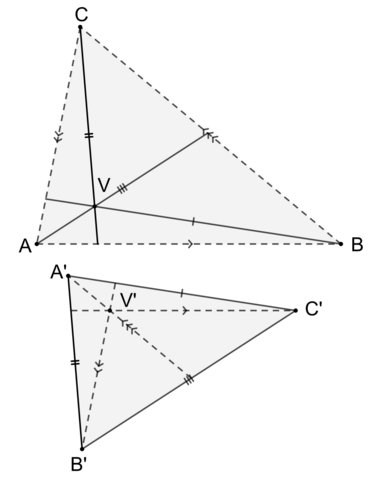
Line segments with identical markings are parallel.
If the sides of the triangle[math]\displaystyle{ A'B'C' }[/math] are parallel to the according cevians of triangle [math]\displaystyle{ ABC }[/math], which are intersecting in a common point [math]\displaystyle{ V' }[/math], then the cevians of triangle [math]\displaystyle{ A'B'C' }[/math], which are parallel to the according sides of triangle [math]\displaystyle{ ABC }[/math] intersect in a common point [math]\displaystyle{ V' }[/math] as well

Maxwell's theorem is the following statement about triangles in the plane.

For a given triangle [math]\displaystyle{ ABC }[/math] and a point [math]\displaystyle{ V }[/math] not on the sides of that triangle construct a second triangle [math]\displaystyle{ A'B'C' }[/math], such that the side [math]\displaystyle{ A'B' }[/math] is parallel to the line segment [math]\displaystyle{ CV }[/math], the side [math]\displaystyle{ A'C' }[/math] is parallel to the line segment [math]\displaystyle{ BV }[/math] and the side [math]\displaystyle{ B'C' }[/math] is parallel to the line segment [math]\displaystyle{ AV }[/math]. Then the parallel to [math]\displaystyle{ AB }[/math] through [math]\displaystyle{ C' }[/math], the parallel to [math]\displaystyle{ BC }[/math] through [math]\displaystyle{ A' }[/math] and the parallel to [math]\displaystyle{ AC }[/math] through [math]\displaystyle{ B' }[/math] intersect in a common point [math]\displaystyle{ V' }[/math].

The theorem is named after the physicist James Clerk Maxwell (1831–1879), who proved it in his work on reciprocal figures, which are of importance in statics.

References

• Daniel Pedoe: Geometry: A Comprehensive Course. Dover, 1970, pp. 35–36, 114–115
• Daniel Pedoe: "On (what should be) a Well-Known Theorem in Geometry." The American Mathematical Monthly, Vol. 74, No. 7 (August – September, 1967), pp. 839–841 (JSTOR)
• Dao Thanh Oai, Cao Mai Doai, Quang Trung, Kien Xuong, Thai Binh: "Generalizations of some famous classical Euclidean geometry theorems." International Journal of Computer Discovered Mathematics, Vol. 1, No. 3, pp. 13–20

External links

• Maxwell's Theorem at cut-the-knot.org