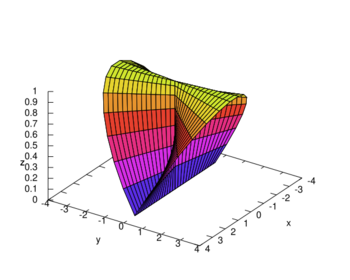
Wallis's conical edge
From HandWiki
Revision as of 06:41, 31 July 2022 by imported>Steve Marsio (link)
Short description: Right conoid ruled surface
In geometry, Wallis's conical edge is a ruled surface given by the parametric equations
- [math]\displaystyle{ x=v\cos u,\quad y=v\sin u,\quad z=c\sqrt{a^2-b^2\cos^2u} }[/math]
where a, b and c are constants.
Wallis's conical edge is also a kind of right conoid. It is named after the English mathematician John Wallis, who was one of the first to use Cartesian methods to study conic sections.[1]
See also
References
- ↑ Abbena, Elsa; Salamon, Simon; Gray, Alfred (21 June 2006). Modern Differential Geometry of Curves and Surfaces with Mathematica, Third Edition. ISBN 9781584884484. https://books.google.com/books?id=owEj9TMYo7IC&dq=John+Wallis+%22conical+edge%22&pg=PA450.
- A. Gray, E. Abbena, S. Salamon, Modern differential geometry of curves and surfaces with Mathematica, 3rd ed. Boca Raton, Florida:CRC Press, 2006. [1] (ISBN 978-1-58488-448-4)
External links
- Wallis's Conical Edge from MathWorld.
 |