Ruled surface
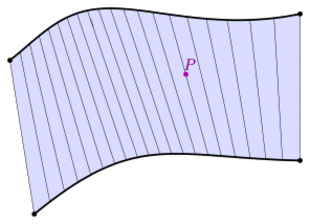
In geometry, a surface S is ruled (also called a scroll) if through every point of S there is a straight line that lies on S. Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space.
A ruled surface can be described as the set of points swept by a moving straight line. For example, a cone is formed by keeping one point of a line fixed whilst moving another point along a circle. A surface is doubly ruled if through every one of its points there are two distinct lines that lie on the surface. The hyperbolic paraboloid and the hyperboloid of one sheet are doubly ruled surfaces. The plane is the only surface which contains at least three distinct lines through each of its points (Fuchs Tabachnikov).
The properties of being ruled or doubly ruled are preserved by projective maps, and therefore are concepts of projective geometry. In algebraic geometry, ruled surfaces are sometimes considered to be surfaces in affine or projective space over a field, but they are also sometimes considered as abstract algebraic surfaces without an embedding into affine or projective space, in which case "straight line" is understood to mean an affine or projective line.
Definition and parametric representation
A two dimensional differentiable manifold is called a ruled surface if it is the union of one parametric family of lines. The lines of this family are the generators of the ruled surface.
A ruled surface can be described by a parametric representation of the form
- (CR) [math]\displaystyle{ \quad \mathbf x(u,v)= {\color{red}\mathbf c(u)} + v\;{\color{blue}\mathbf r(u)}\ ,\ v\in \R \ , }[/math].
Any curve [math]\displaystyle{ \;v\mapsto \mathbf x(u_0,v)\; }[/math] with fixed parameter [math]\displaystyle{ u=u_0 }[/math] is a generator (line) and the curve [math]\displaystyle{ \; u\mapsto \mathbf c(u) \; }[/math] is the directrix of the representation. The vectors [math]\displaystyle{ \; \mathbf r(u)\ne \bf 0\; }[/math] describe the directions of the generators.
The directrix may collapse to a point (in case of a cone, see example below).
Alternatively the ruled surface (CR) can be described by
- (CD) [math]\displaystyle{ \quad \mathbf x(u,v)= (1-v)\;{\color{red}\mathbf c(u)} + v\; {\color{green}\mathbf d(u)}\ }[/math]
with the second directrix [math]\displaystyle{ \; \mathbf d(u)= \mathbf c(u) + \mathbf r(u)\; }[/math].
Alternatively, one can start with two non intersecting curves [math]\displaystyle{ \mathbf c(u), \mathbf d(u) }[/math] as directrices, and get by (CD) a ruled surface with line directions [math]\displaystyle{ \; \mathbf r(u)= \mathbf d(u) - \mathbf c(u)\ . }[/math]
For the generation of a ruled surface by two directrices (or one directrix and the vectors of line directions) not only the geometric shape of these curves are essential but also the special parametric representations of them influence the shape of the ruled surface (see examples a), d)).
For theoretical investigations representation (CR) is more advantageous, because the parameter [math]\displaystyle{ v }[/math] appears only once.
Examples
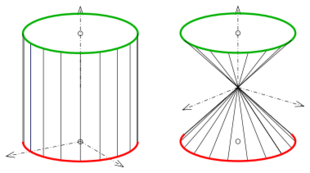
Right circular cylinder
[math]\displaystyle{ \ x^2+y^2=a^2\ }[/math]:
- [math]\displaystyle{ \mathbf x(u,v)=(a\cos u,a\sin u,v)^T }[/math]
- [math]\displaystyle{ = {\color{red}(a\cos u,a\sin u,0)^T}\; +\; v\;{\color{blue}(0,0,1)^T} }[/math]
- [math]\displaystyle{ = (1-v)\;{\color{red}(a\cos u,a\sin u,0)^T}\; + \; v\;{\color{green}(a\cos u,a\sin u,1)^T} \ . }[/math]
with
- [math]\displaystyle{ \mathbf c(u) =(a\cos u,a\sin u,0)^T\ , \ \mathbf r(u)=(0,0,1)^T \ , \ \mathbf d(u)= (a\cos u,a\sin u,1)^T \ . }[/math]
Right circular cone
[math]\displaystyle{ \ x^2+y^2=z^2\ }[/math]:
- [math]\displaystyle{ \mathbf x(u,v)=(\cos u,\sin u,1)^T\; +\; v\;(\cos u,\sin u,1)^T }[/math]
- [math]\displaystyle{ = (1-v)\;(\cos u,\sin u,1)^T\; + \; v\;(2\cos u,2\sin u,2)^T . }[/math]
with [math]\displaystyle{ \quad \mathbf c(u) =(\cos u,\sin u,1)^T\; = \; \mathbf r(u) \ , \quad \mathbf d(u)= (2\cos u,2\sin u,2)^T \ . }[/math]
In this case one could have used the apex as the directrix, i.e.: [math]\displaystyle{ \ \mathbf c(u) = (0,0,0)^T\ }[/math] and [math]\displaystyle{ \ \mathbf r(u)=(\cos u,\sin u,1)^T\ }[/math] as the line directions.
For any cone one can choose the apex as the directrix. This case shows: The directrix of a ruled surface may degenerate to a point.
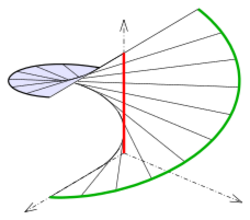
Helicoid
- [math]\displaystyle{ \mathbf x(u,v)=\;(v\cos u,v\sin u, ku)^T\; }[/math]
- [math]\displaystyle{ = \; (0,0,ku)^T \; +\; v\;(\cos u, \sin u,0)^T\ }[/math]
- [math]\displaystyle{ = \; (1-v)\;(0,0,ku)^T \; + \; v\; (\cos u,\sin u, ku)^T \ . }[/math]
The directrix [math]\displaystyle{ \ \mathbf c(u) =(0,0,ku)^T\; }[/math] is the z-axis, the line directions are [math]\displaystyle{ \; \mathbf r(u) =\ (\cos u, \sin u,0)^T \; }[/math] and the second directrix [math]\displaystyle{ \ \mathbf d(u)=(\cos u,\sin u, ku)^T \ }[/math] is a helix.
The helicoid is a special case of the ruled generalized helicoids.
Cylinder, cone and hyperboloids
The parametric representation
- [math]\displaystyle{ \mathbf x(u,v)= (1-v)\;(\cos (u-\varphi),\sin (u-\varphi),-1)^T\; + \; v\;(\cos (u+\varphi),\sin(u+\varphi),1)^T }[/math]
has two horizontal circles as directrices. The additional parameter [math]\displaystyle{ \varphi }[/math] allows to vary the parametric representations of the circles. For
- [math]\displaystyle{ \varphi=0 \ }[/math] one gets the cylinder [math]\displaystyle{ x^2+y^2=1 }[/math], for
- [math]\displaystyle{ \varphi=\pi/2 \ }[/math] one gets the cone [math]\displaystyle{ x^2+y^2=z^2 }[/math] and for
- [math]\displaystyle{ 0\lt \varphi\lt \pi/2 \ }[/math] one gets a hyperboloid of one sheet with equation [math]\displaystyle{ \ \tfrac{x^2+y^2}{a^2}-\tfrac{z^2}{c^2}=1 \ }[/math] and the semi axes [math]\displaystyle{ \ a=\cos\varphi\;,\; c=\cot\varphi }[/math].
A hyperboloid of one sheet is a doubly ruled surface.
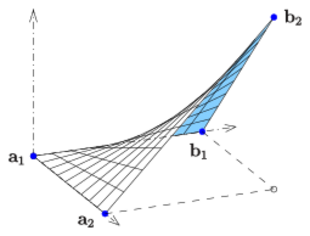
Hyperbolic paraboloid
If the two directrices in (CD) are the lines
- [math]\displaystyle{ \mathbf c(u) =(1-u)\mathbf a_1 + u\mathbf a_2, \quad \mathbf d(u)=(1-u)\mathbf b_1 + u\mathbf b_2 }[/math]
one gets
- [math]\displaystyle{ \mathbf x(u,v)=(1-v)\big((1-u)\mathbf a_1 + u\mathbf a_2\big)\ +\ v\big((1-u)\mathbf b_1 + u\mathbf b_2\big)\ }[/math],
which is the hyperbolic paraboloid that interpolates the 4 points [math]\displaystyle{ \ \mathbf a_1,\;\mathbf a_2,\;\mathbf b_1,\;\mathbf b_2\ }[/math] bilinearly.[1]
Obviously the ruled surface is a doubly ruled surface, because any point lies on two lines of the surface.
For the example shown in the diagram:
- [math]\displaystyle{ \ \mathbf a_1=(0,0,0)^T,\;\mathbf a_2=(1,0,0)^T,\;\mathbf b_1=(0,1,0)^T,\;\mathbf b_2=(1,1,1)^T\ }[/math].
The hyperbolic paraboloid has the equation [math]\displaystyle{ z=xy }[/math].
Möbius strip
The ruled surface
- [math]\displaystyle{ \mathbf x(u,v)= \mathbf c(u) + v\;\mathbf r(u) }[/math]
with
- [math]\displaystyle{ \mathbf c(u) =(\cos2u,\sin2u,0)^T\ }[/math] (circle as directrix),
- [math]\displaystyle{ \mathbf r(u)=( \cos u \cos 2 u , \cos u \sin 2 u, \sin u )^T \ , \quad 0\le u\lt \pi\ , }[/math]
contains a Möbius strip.
The diagram shows the Möbius strip for [math]\displaystyle{ -0.3\le v \le 0.3 }[/math].
A simple calculation shows [math]\displaystyle{ \det(\mathbf \dot c(0)\;,\;\mathbf \dot r(0)\;, \;\mathbf r(0)) \; \ne \; 0 \ }[/math] (see next section). Hence the given realization of a Möbius strip is not developable. But there exist developable Möbius strips.[2]
Further examples
Tangent planes, developable surfaces
For the considerations below any necessary derivative is assumed to exist.
For the determination of the normal vector at a point one needs the partial derivatives of the representation [math]\displaystyle{ \quad \mathbf x(u,v)= \mathbf c(u) + v\;\mathbf r(u) }[/math] :
- [math]\displaystyle{ \mathbf x_u= \mathbf \dot c(u)+ v\;\mathbf \dot r(u)\ }[/math] ,[math]\displaystyle{ \quad \mathbf x_v= \;\mathbf r(u) }[/math]
Hence the normal vector is
- [math]\displaystyle{ \mathbf n= \mathbf x_u \times \mathbf x_v = \mathbf \dot c\times \mathbf r + v( \mathbf \dot r \times \mathbf r) \ . }[/math]
Because of [math]\displaystyle{ \mathbf n \cdot \mathbf r = 0 }[/math] (A mixed product with two equal vectors is always 0 !), vector [math]\displaystyle{ \mathbf r (u_0) }[/math] is a tangent vector at any point [math]\displaystyle{ \mathbf x(u_0,v) }[/math]. The tangent planes along this line are all the same, if [math]\displaystyle{ \mathbf \dot r \times \mathbf r }[/math] is a multiple of [math]\displaystyle{ \mathbf \dot c\times \mathbf r }[/math] . This is possible only, if the three vectors [math]\displaystyle{ \mathbf \dot c\; ,\; \mathbf \dot r\;,\; \mathbf r\ }[/math] lie in a plane, i.e. they are linearly dependent. The linear dependency of three vectors can be checked using the determinant of these vectors:
- The tangent planes along the line [math]\displaystyle{ \mathbf x(u_0,v)= \mathbf c(u_0) + v\;\mathbf r(u_0) }[/math] are equal, if
- [math]\displaystyle{ \det(\mathbf \dot c(u_0)\;,\;\mathbf \dot r(u_0)\;, \;\mathbf r(u_0)) \; = \; 0 \ . }[/math]
The importance of this determinant condition shows the following statement:
- A ruled surface [math]\displaystyle{ \quad \mathbf x(u,v)= \mathbf c(u) + v\;\mathbf r(u) }[/math] is developable into a plane, if for every point the Gauss curvature vanishes. This is exactly the case if
- [math]\displaystyle{ \det(\mathbf \dot c\;,\;\mathbf \dot r\;, \;\mathbf r) \; = \; 0 \quad }[/math]
- at every point is true.[3]
The generators of any ruled surface coalesce with one family of its asymptotic lines. For developable surfaces they also form one family of its lines of curvature. It can be shown that any developable surface is a cone, a cylinder or a surface formed by all tangents of a space curve.[4]
Application and history of developable surfaces
The determinant condition for developable surfaces is used to determine numerically developable connections between space curves (directrices). The diagram shows a developable connection between two ellipses contained in different planes (one horizontal, the other vertical) and its development.[5]
An impression of the usage of developable surfaces in Computer Aided Design (CAD) is given in Interactive design of developable surfaces[6]
A historical survey on developable surfaces can be found in Developable Surfaces: Their History and Application[7]
Ruled surfaces in algebraic geometry
In algebraic geometry, ruled surfaces were originally defined as projective surfaces in projective space containing a straight line through any given point. This immediately implies that there is a projective line on the surface through any given point, and this condition is now often used as the definition of a ruled surface: ruled surfaces are defined to be abstract projective surfaces satisfying this condition that there is a projective line through any point. This is equivalent to saying that they are birational to the product of a curve and a projective line. Sometimes a ruled surface is defined to be one satisfying the stronger condition that it has a fibration over a curve with fibers that are projective lines. This excludes the projective plane, which has a projective line though every point but cannot be written as such a fibration.
Ruled surfaces appear in the Enriques classification of projective complex surfaces, because every algebraic surface of Kodaira dimension [math]\displaystyle{ -\infty }[/math] is a ruled surface (or a projective plane, if one uses the restrictive definition of ruled surface). Every minimal projective ruled surface other than the projective plane is the projective bundle of a 2-dimensional vector bundle over some curve. The ruled surfaces with base curve of genus 0 are the Hirzebruch surfaces.
Ruled surfaces in architecture
Doubly ruled surfaces are the inspiration for curved hyperboloid structures that can be built with a latticework of straight elements, namely:
- Hyperbolic paraboloids, such as saddle roofs.
- Hyperboloids of one sheet, such as cooling towers and some trash bins.
The RM-81 Agena rocket engine employed straight cooling channels that were laid out in a ruled surface to form the throat of the nozzle section.
Cooling hyperbolic towers at Didcot Power Station, UK; the surface can be doubly ruled.
Doubly ruled water tower with toroidal tank, by Jan Bogusławski in Ciechanów, Poland
A hyperboloid Kobe Port Tower, Kobe, Japan, with a double ruling.
Hyperboloid water tower, 1896 in Nizhny Novgorod.
The gridshell of Shukhov Tower in Moscow, whose sections are doubly ruled.
A ruled helicoid spiral staircase inside Cremona's Torrazzo.
Village church in Selo, Slovenia: both the roof (conical) and the wall (cylindrical) are ruled surfaces.
A hyperbolic paraboloid roof of Warszawa Ochota railway station in Warsaw, Poland.
A ruled conical hat.
Corrugated roof tiles ruled by parallel lines in one direction, and sinusoidal in the perpendicular direction
Construction of a planar surface by ruling (screeding) concrete
References
- ↑ G. Farin: Curves and Surfaces for Computer Aided Geometric Design, Academic Press, 1990, ISBN:0-12-249051-7, p. 250
- ↑ W. Wunderlich: Über ein abwickelbares Möbiusband, Monatshefte für Mathematik 66, 1962, S. 276-289.
- ↑ W. Kühnel: Differentialgeometrie, p. 58–60
- ↑ G. Farin: p. 380
- ↑ E. Hartmann: Geometry and Algorithms for CAD, lecture note, TU Darmstadt, p. 113
- ↑ Tang, Bo, Wallner, Pottmann: Interactive design of developable surfaces, ACM Trans. Graph. (MONTH 2015), DOI: 10.1145/2832906
- ↑ Snezana Lawrence: Developable Surfaces: Their History and Application, in Nexus Network Journal 13(3) · October 2011, doi:10.1007/s00004-011-0087-z
- Do Carmo, Manfredo P. : Differential Geometry of Curves and Surfaces, Prentice-Hall; 1 edition, 1976 ISBN:978-0132125895
- Barth, Wolf P.; Hulek, Klaus; Peters, Chris A.M.; Van de Ven, Antonius (2004), Compact Complex Surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge., 4, Springer-Verlag, Berlin, doi:10.1007/978-3-642-57739-0, ISBN 978-3-540-00832-3
- Beauville, Arnaud (1996), Complex algebraic surfaces, London Mathematical Society Student Texts, 34 (2nd ed.), Cambridge University Press, doi:10.1017/CBO9780511623936, ISBN 978-0-521-49510-3
- Edge, W. L. (1931), The Theory of Ruled Surfaces, Cambridge University Press, https://archive.org/details/theoryofruledsur029537mbp. Review: Bulletin of the American Mathematical Society 37 (1931), 791-793, doi:10.1090/S0002-9904-1931-05248-4
- Fuchs, D.; Tabachnikov, Serge (2007), "16.5 There are no non-planar triply ruled surfaces", Mathematical Omnibus: Thirty Lectures on Classic Mathematics, American Mathematical Society, p. 228, ISBN 9780821843161, https://books.google.com/books?id=IiG9AwAAQBAJ&pg=PA228.
- Li, Ta-chʻien (ed.) (2011), Problems and Solutions in Mathematics, 3103 (2nd ed.), World Scientific Publishing Company, ISBN 9789810234805, https://books.google.com/books?id=lrMOjbLhR2IC&pg=PA156.
- Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, ISBN 978-0-8284-1087-8.
- Hazewinkel, Michiel, ed. (2001), "Ruled surface", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=R/r082790
- Sharp, John (2008), D-Forms: surprising new 3-D forms from flat curved shapes, Tarquin, ISBN 978-1-899618-87-3. Review: Séquin, Carlo H. (2009), Journal of Mathematics and the Arts 3: 229–230, doi:10.1080/17513470903332913
External links
- Weisstein, Eric W.. "Ruled Surface". http://mathworld.wolfram.com/RuledSurface.html.
- Ruled surface pictures from the University of Arizona
- Examples of developable surfaces on the Rhino3DE website
 |  |
