Flexible polyhedron

Steffen's polyhedron, the simplest possible non-self-crossing flexible polyhedron

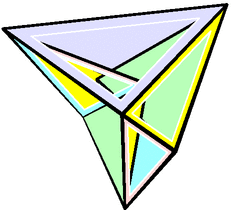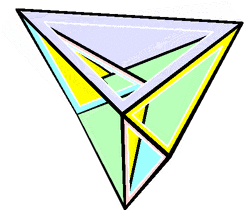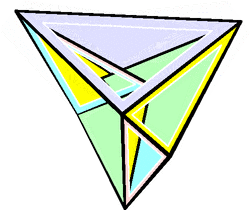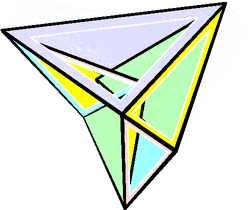
In geometry, a flexible polyhedron is a polyhedral surface without any boundary edges, whose shape can be continuously changed while keeping the shapes of all of its faces unchanged. The Cauchy rigidity theorem shows that in dimension 3 such a polyhedron cannot be convex (this is also true in higher dimensions).

The first examples of flexible polyhedra, now called Bricard octahedra, were discovered by Raoul Bricard (1897). They are self-intersecting surfaces isometric to an octahedron. The first example of a flexible non-self-intersecting surface in [math]\displaystyle{ \mathbb{R}^3 }[/math], the Connelly sphere, was discovered by Robert Connelly (1977). Steffen's polyhedron is another non-self-intersecting flexible polyhedron derived from Bricard's octahedra.

Bellows conjecture

In the late 1970s Connelly and D. Sullivan formulated the bellows conjecture stating that the volume of a flexible polyhedron is invariant under flexing. This conjecture was proved for polyhedra homeomorphic to a sphere by I. Kh. Sabitov (1995) using elimination theory, and then proved for general orientable 2-dimensional polyhedral surfaces by Robert Connelly, I. Sabitov, and Anke Walz (1997). The proof extends Piero della Francesca's formula for the volume of a tetrahedron to a formula for the volume of any polyhedron. The extended formula shows that the volume must be a root of a polynomial whose coefficients depend only on the lengths of the polyhedron's edges. Since the edge lengths cannot change as the polyhedron flexes, the volume must remain at one of the finitely many roots of the polynomial, rather than changing continuously.

Scissor congruence

Connelly conjectured that the Dehn invariant of a flexible polyhedron is invariant under flexing. This was known as the strong bellows conjecture or (after it was proven in 2018) the strong bellows theorem. Because all configurations of a flexible polyhedron have both the same volume and the same Dehn invariant, they are scissors congruent to each other, meaning that for any two of these configurations it is possible to dissect one of them into polyhedral pieces that can be reassembled to form the other. The total mean curvature of a flexible polyhedron, defined as the sum of the products of edge lengths with exterior dihedral angles, is a function of the Dehn invariant that is also known to stay constant while a polyhedron flexes.

Generalizations

Flexible 4-polytopes in 4-dimensional Euclidean space and 3-dimensional hyperbolic space were studied by Hellmuth Stachel (2000). In dimensions [math]\displaystyle{ n\geq 5 }[/math], flexible polytopes were constructed by (Gaifullin 2014).

See also

• Flexagon
• Rigid origami

References

Primary sources

• Alexander, Ralph (1985), "Lipschitzian mappings and total mean curvature of polyhedral surfaces. I", Transactions of the American Mathematical Society 288 (2): 661–678, doi:10.2307/1999957 .
• Alexandrov, Victor (2010), "The Dehn invariants of the Bricard octahedra", Journal of Geometry 99 (1–2): 1–13, doi:10.1007/s00022-011-0061-7 .
• Bricard, R. (1897), "Mémoire sur la théorie de l'octaèdre articulé", J. Math. Pures Appl. 5 (3): 113–148, http://portail.mathdoc.fr/JMPA/afficher_notice.php?id=JMPA_1897_5_3_A5_0, retrieved 2008-07-27 
• Connelly, Robert (1977), "A counterexample to the rigidity conjecture for polyhedra", Publications Mathématiques de l'IHÉS 47 (47): 333–338, doi:10.1007/BF02684342, ISSN 1618-1913, http://www.numdam.org/item?id=PMIHES_1977__47__333_0 
• Connelly, Robert; Sabitov, I.; Walz, Anke (1997), "The bellows conjecture", Beiträge zur Algebra und Geometrie 38 (1): 1–10, ISSN 0138-4821, https://emis.de/journals/BAG/vol.38/no.1/1.html 
• Gaifullin, Alexander A. (2014), "Flexible cross-polytopes in spaces of constant curvature", Proceedings of the Steklov Institute of Mathematics 286 (1): 77–113, doi:10.1134/S0081543814060066 .
• Gaĭfullin, A. A.; Ignashchenko, L. S. (2018), "Dehn invariant and scissors congruence of flexible polyhedra", Trudy Matematicheskogo Instituta Imeni V. A. Steklova 302 (Topologiya i Fizika): 143–160, doi:10.1134/S0371968518030068, ISBN 5-7846-0147-4 .
• Sabitov, I. Kh. (1995), "On the problem of the invariance of the volume of a deformable polyhedron", Rossiĭskaya Akademiya Nauk. Moskovskoe Matematicheskoe Obshchestvo. Uspekhi Matematicheskikh Nauk 50 (2): 223–224, ISSN 0042-1316 
• A. Prékopa, ed. (2006), "Flexible octahedra in the hyperbolic space", Non-Euclidean geometries (János Bolyai memorial volume), Mathematics and its Applications, 581, New York: Springer, pp. 209–225, doi:10.1007/0-387-29555-0_11, ISBN 978-0-387-29554-1 .
• "Flexible cross-polytopes in the Euclidean 4-space", Journal for Geometry and Graphics 4 (2): 159–167, 2000, http://www.geometrie.tuwien.ac.at/stachel/cross.pdf .

Secondary sources

• "The rigidity of polyhedral surfaces", Mathematics Magazine 52 (5): 275–283, 1979, doi:10.2307/2689778 .
• Klarner, David A., ed. (1981), "Flexing surfaces", The Mathematical Gardner, Springer, pp. 79–89, doi:10.1007/978-1-4684-6686-7_10, ISBN 978-1-4684-6688-1 .
• "Rigidity", Handbook of convex geometry, Vol. A, B, Amsterdam: North-Holland, 1993, pp. 223–271, http://www.math.cornell.edu/~web7620/Rigidity-Connelly.pdf .
• "23.2 Flexible polyhedra", Geometric Folding Algorithms: Linkages, origami, polyhedra, Cambridge University Press, Cambridge, 2007, pp. 345–348, doi:10.1017/CBO9780511735172, ISBN 978-0-521-85757-4 .
• Fuchs, Dmitry; Tabachnikov, Serge (2007), "Lecture 25. Flexible polyhedra", Mathematical Omnibus: Thirty lectures on classic mathematics, Providence, RI: American Mathematical Society, pp. 345–360, doi:10.1090/mbk/046, ISBN 978-0-8218-4316-1 

External links

• Eric W. Weisstein, Flexible polyhedron (Bellows conjecture) at MathWorld.