Adams spectral sequence

In mathematics, the Adams spectral sequence is a spectral sequence introduced by J. Frank Adams (1958) which computes the stable homotopy groups of topological spaces. Like all spectral sequences, it is a computational tool; it relates homology theory to what is now called stable homotopy theory. It is a reformulation using homological algebra, and an extension, of a technique called 'killing homotopy groups' applied by the French school of Henri Cartan and Jean-Pierre Serre.

Motivation

For everything below, once and for all, we fix a prime p. All spaces are assumed to be CW complexes. The ordinary cohomology groups [math]\displaystyle{ H^*(X) }[/math] are understood to mean [math]\displaystyle{ H^*(X; \Z/p\Z) }[/math].

The primary goal of algebraic topology is to try to understand the collection of all maps, up to homotopy, between arbitrary spaces X and Y. This is extraordinarily ambitious: in particular, when X is [math]\displaystyle{ S^n }[/math], these maps form the nth homotopy group of Y. A more reasonable (but still very difficult!) goal is to understand the set [math]\displaystyle{ [X, Y] }[/math] of maps (up to homotopy) that remain after we apply the suspension functor a large number of times. We call this the collection of stable maps from X to Y. (This is the starting point of stable homotopy theory; more modern treatments of this topic begin with the concept of a spectrum. Adams' original work did not use spectra, and we avoid further mention of them in this section to keep the content here as elementary as possible.)

The set [math]\displaystyle{ [X, Y] }[/math] turns out to be an abelian group, and if X and Y are reasonable spaces this group is finitely generated. To figure out what this group is, we first isolate a prime p. In an attempt to compute the p-torsion of [math]\displaystyle{ [X, Y] }[/math], we look at cohomology: send [math]\displaystyle{ [X, Y] }[/math] to Hom(H^*(Y), H^*(X)). This is a good idea because cohomology groups are usually tractable to compute.

The key idea is that [math]\displaystyle{ H^*(X) }[/math] is more than just a graded abelian group, and more still than a graded ring (via the cup product). The representability of the cohomology functor makes H^*(X) a module over the algebra of its stable cohomology operations, the Steenrod algebra A. Thinking about H^*(X) as an A-module forgets some cup product structure, but the gain is enormous: Hom(H^*(Y), H^*(X)) can now be taken to be A-linear! A priori, the A-module sees no more of [X, Y] than it did when we considered it to be a map of vector spaces over F_p. But we can now consider the derived functors of Hom in the category of A-modules, Ext_A^r(H^*(Y), H^*(X)). These acquire a second grading from the grading on H^*(Y), and so we obtain a two-dimensional "page" of algebraic data. The Ext groups are designed to measure the failure of Hom's preservation of algebraic structure, so this is a reasonable step.

The point of all this is that A is so large that the above sheet of cohomological data contains all the information we need to recover the p-primary part of [X, Y], which is homotopy data. This is a major accomplishment because cohomology was designed to be computable, while homotopy was designed to be powerful. This is the content of the Adams spectral sequence.

Classical formulation

Formulation for computing homotopy groups of spectra

The classical Adams spectral sequence can be stated for any connective spectrum [math]\displaystyle{ X }[/math] of finite type, meaning [math]\displaystyle{ \pi_i(X)=0 }[/math] for [math]\displaystyle{ i \lt 0 }[/math] and [math]\displaystyle{ \pi_i(X) }[/math] is a finitely generated Abelian group in each degree. Then, there is a spectral sequence [math]\displaystyle{ E_*^{*,*}(X) }[/math] such that

1. [math]\displaystyle{ E_2^{s,t} = \text{Ext}_{A_p}^{s,t}(H^*(X), \Z/p) }[/math] for [math]\displaystyle{ A_p }[/math] the mod [math]\displaystyle{ p }[/math] Steenrod algebra
2. For [math]\displaystyle{ X }[/math] of finite type, [math]\displaystyle{ E_\infty^{*,*} }[/math] is a bigraded group associated with a filtration of [math]\displaystyle{ \pi_*(X)\otimes \Z_p }[/math] (the p-adic integers)

Note that this implies for [math]\displaystyle{ X = \mathbb{S} }[/math], this computes the [math]\displaystyle{ p }[/math]-torsion of the homotopy groups of the sphere spectrum, i.e. the stable homotopy groups of the spheres. Also, because for any CW-complex [math]\displaystyle{ Y }[/math] we can consider the suspension spectrum [math]\displaystyle{ \Sigma^\infty Y }[/math], this gives the statement of the previous formulation as well.

This statement generalizes a little bit further by replacing the [math]\displaystyle{ \mathcal{A}_p }[/math]-module [math]\displaystyle{ \mathbb{Z}/p }[/math] with the cohomology groups [math]\displaystyle{ H^*(Y) }[/math] for some connective spectrum [math]\displaystyle{ Y }[/math] (or topological space [math]\displaystyle{ Y }[/math]). This is because the construction of the spectral sequence uses a "free" resolution of [math]\displaystyle{ H^*(X) }[/math] as an [math]\displaystyle{ \mathcal{A}_p }[/math]-module, hence we can compute the Ext groups with [math]\displaystyle{ H^*(Y) }[/math] as the second entry. We therefore get a spectral sequence with [math]\displaystyle{ E_2 }[/math]-page given by

[math]\displaystyle{ E_2^{t,s} = \text{Ext}_{\mathcal{A}_p}^{s,t}(H^*(X),H^*(Y)) }[/math]

which has the convergence property of being isomorphic to the graded pieces of a filtration of the [math]\displaystyle{ p }[/math]-torsion of the stable homotopy group of homotopy classes of maps between [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], that is

[math]\displaystyle{ E_2^{s,t} \Rightarrow \pi_k^{\mathbb{S}}([X,Y])\otimes \mathbb{Z}_{p} }[/math]

Spectral sequence for the stable homotopy groups of spheres

For example, if we let both spectra be the sphere spectrum, so [math]\displaystyle{ X = Y = \mathbb{S} }[/math], then the Adams spectral sequence has the convergence property

[math]\displaystyle{ E_2^{t,s} = \text{Ext}_{\mathcal{A}_p}^{s,t}(H^*(\mathbb{S}),H^*(\mathbb{S})) \Rightarrow \pi_*(\mathbb{S})\otimes \mathbb{Z}_p }[/math]

giving a technical tool for approaching a computation of the stable homotopy groups of spheres. It turns out that many of the first terms can be computed explicitly from purely algebraic information^{pp 23–25}. Also note that we can rewrite [math]\displaystyle{ H^*(\mathbb{S}) = \mathbb{Z}/p }[/math], so the [math]\displaystyle{ E_2 }[/math]-page is

[math]\displaystyle{ E_2^{t,s} = \operatorname{Ext}_{\mathcal{A}_p}^{s,t}(\mathbb{Z}/p,\mathbb{Z}/p) \Rightarrow \pi_*(\mathbb{S})\otimes \mathbb{Z}_p }[/math]

We include this calculation information below for [math]\displaystyle{ p=2 }[/math].

Ext terms from the resolution

Given the Adams resolution

[math]\displaystyle{ \cdots \to H^*(F_2) \to H^*(F_1) \to H^*(F_0) \to H^*(X) }[/math]

we have the [math]\displaystyle{ E_1 }[/math]-terms as

[math]\displaystyle{ E_1^{s,t} = \operatorname{Hom}^t_{\mathcal{A}_p}(H^*(F_s),H^*(Y)) }[/math]

for the graded Hom-groups. Then the [math]\displaystyle{ E_1 }[/math]-page can be written as

[math]\displaystyle{ E_1 = \begin{array}{c|ccc} 3 & \vdots & \vdots & \vdots\\ 2 & \text{Hom}^2(H^*(F_0), H^*(Y)) & \text{Hom}^2(H^*(F_1), H^*(Y)) & \text{Hom}^2(H^*(F_2), H^*(Y)) & \cdots \\ 1 & \text{Hom}^1(H^*(F_0), H^*(Y)) & \text{Hom}^1(H^*(F_1), H^*(Y)) & \text{Hom}^1(H^*(F_2), H^*(Y)) & \cdots \\ 0 & \text{Hom}^0(H^*(F_0), H^*(Y)) & \text{Hom}^0(H^*(F_1), H^*(Y)) & \text{Hom}^0(H^*(F_2), H^*(Y)) & \cdots \\ \hline & 0 & 1 & 2 \end{array} }[/math]

so the degree of [math]\displaystyle{ s }[/math] can be thought of how "deep" in the Adams resolution we go before we can find the generators.

Calculations

The sequence itself is not an algorithmic device, but lends itself to problem solving in particular cases.

Grading of the Differential

The [math]\displaystyle{ r }[/math]th Adams differential always goes to the left 1, and up [math]\displaystyle{ r }[/math]. That is,

[math]\displaystyle{ d_r \colon E_r^{s, t} \to E_r^{s+r,t+r-1} }[/math].

Examples with Eilenberg–Maclane spectra

Some of the simplest calculations are with Eilenberg–Maclane spectra such as [math]\displaystyle{ X = H\Z }[/math] and [math]\displaystyle{ X = H\Z/(p^k) }[/math]. For the first case, we have the [math]\displaystyle{ E_1 }[/math] page

[math]\displaystyle{ E_1^{s,t} = \begin{cases} \Z/p & \text{ if } t = s \\ 0 & \text{ otherwise } \end{cases} }[/math]

giving a collapsed spectral sequence, hence [math]\displaystyle{ E_1 = E_\infty }[/math]. This can be rewritten as

[math]\displaystyle{ \text{Ext}^{s,t}_{\mathcal{A}_p}(H^*(H\Z), \Z/p) = \begin{cases} \Z/p & \text{ if } t = s \\ 0 & \text{ if } t \neq s \end{cases} }[/math]

giving the [math]\displaystyle{ E_2 }[/math]-page. For the other case, note there is a cofiber sequence

[math]\displaystyle{ H\Z\xrightarrow{\cdot p^k} H\Z \to H\Z/p^k \to \Sigma H\Z }[/math]

which ends up giving a splitting in cohomology, so [math]\displaystyle{ H^*(H\Z/p^k) = H^*(H\Z)\oplus H^*(\Sigma H\Z) }[/math] as [math]\displaystyle{ \mathcal{A}_p }[/math]-modules. Then, the [math]\displaystyle{ E_2 }[/math]-page of [math]\displaystyle{ H^*(H\Z/p) }[/math] can be read as

[math]\displaystyle{ E_2^{s,t} = \begin{cases} \Z/p & \text{if } t-s = 0,1 \\ 0 & \text{otherwise } \end{cases} }[/math]

The expected [math]\displaystyle{ E_\infty }[/math]-page is

[math]\displaystyle{ E_\infty^{s,t} = \begin{cases} \mathbb{Z}/p^k & \text{ if } t = s \\ 0 & \text{ otherwise } \end{cases} }[/math].

The only way for this spectral sequence to converge to this page is if is there are non-trivial differentials supported on every element with Adams grading [math]\displaystyle{ (s, s+1) }[/math].

Other applications

Adams' original use for his spectral sequence was the first proof of the Hopf invariant 1 problem: [math]\displaystyle{ \R^n }[/math] admits a division algebra structure only for n = 1, 2, 4, or 8. He subsequently found a much shorter proof using cohomology operations in K-theory.

The Thom isomorphism theorem relates differential topology to stable homotopy theory, and this is where the Adams spectral sequence found its first major use: in 1960, John Milnor and Sergei Novikov used the Adams spectral sequence to compute the coefficient ring of complex cobordism. Further, Milnor and C. T. C. Wall used the spectral sequence to prove Thom's conjecture on the structure of the oriented cobordism ring: two oriented manifolds are cobordant if and only if their Pontryagin and Stiefel–Whitney numbers agree.

Stable homotopy groups of spheres

Visual diagram demonstrating the [math]\displaystyle{ E_2 }[/math] page of the Adams spectral sequence computing the stable homotopy groups of spheres. The dots represent elements left over from the [math]\displaystyle{ E_1 }[/math] page and the diagonal lines moving up and to the left represent various differentials in the spectral sequence. The differential [math]\displaystyle{ d_r }[/math] moves one unit to the left and [math]\displaystyle{ r }[/math] units upward. The vertical lines are used as a book-keeping tool for determining the structure of the torsion groups. Moreover, they represent multiplication by [math]\displaystyle{ 2 }[/math]. The lines moving up and right by one unit represent multiplication by [math]\displaystyle{ h_1 }[/math].

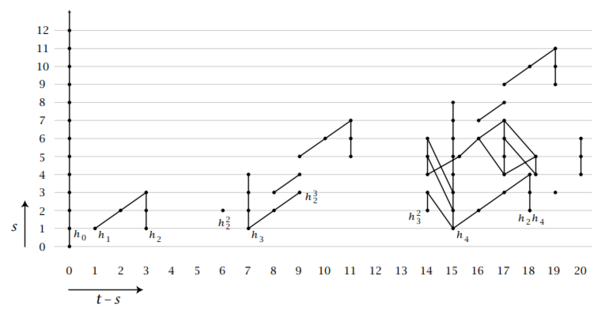
Using the spectral sequence above for [math]\displaystyle{ X = Y = \mathbb{S} }[/math] we can compute several terms explicitly, giving some of the first stable homotopy groups of spheres. For [math]\displaystyle{ p=2 }[/math] this amounts to looking at the [math]\displaystyle{ E_2 }[/math]-page with

[math]\displaystyle{ E_2^{s,t} = \text{Ext}_{\mathcal{A}_2}^{s,t}(\mathbb{Z}/2,\mathbb{Z}/2) }[/math]

This can be done by first looking at the Adams resolution of [math]\displaystyle{ \mathbb{Z}/2 }[/math]. Since [math]\displaystyle{ \mathbb{Z}/2 }[/math] is in degree [math]\displaystyle{ 0 }[/math], we have a surjection

[math]\displaystyle{ \mathcal{A}_2\cdot \iota \to \mathbb{Z}/2 }[/math]

where [math]\displaystyle{ \mathcal{A}_2 }[/math] has a generator in degree [math]\displaystyle{ 0 }[/math] denoted [math]\displaystyle{ \iota }[/math]. The kernel [math]\displaystyle{ K_0 }[/math] consists of all elements [math]\displaystyle{ Sq^I\iota }[/math] for admissible monomials [math]\displaystyle{ Sq^I }[/math] generating [math]\displaystyle{ \mathcal{A}_2 }[/math], hence we have a map

[math]\displaystyle{ \bigoplus_{I \text{ admissible}} \mathcal{A}_2\cdot Sq^I\iota \to K_0 }[/math]

and we denote each of the generators mapping to [math]\displaystyle{ Sq^i\iota }[/math] in the direct sum as [math]\displaystyle{ \alpha_i }[/math], and the rest of the generators as [math]\displaystyle{ Sq^I\alpha_j }[/math] for some [math]\displaystyle{ j }[/math]. For example,

[math]\displaystyle{ \begin{align} \alpha_1 \mapsto Sq^1\iota & &Sq^2\alpha_1 \mapsto Sq^{2,1}\iota \\ \alpha_2 \mapsto Sq^2\iota & & Sq^1\alpha_2 \mapsto Sq^3\iota \\ \alpha_4 \mapsto Sq^4\iota & & Sq^3\alpha_1 \mapsto Sq^{3,1}\iota \\ \alpha_8 \mapsto Sq^8 & & Sq^2\alpha_2 \mapsto Sq^{3,1}\iota \end{align} }[/math]

Notice that the last two elements of [math]\displaystyle{ \alpha_i }[/math] map to the same element, which follows from the Adem relations. Also, there are elements in the kernel, such as [math]\displaystyle{ Sq^1\alpha_1 }[/math] since

[math]\displaystyle{ Sq^1\alpha_1 \mapsto Sq^1Sq^1\iota = 0 }[/math]

because of the Adem relation. We call the generator of this element in [math]\displaystyle{ F_2 }[/math], [math]\displaystyle{ \beta_2 }[/math]. We can apply the same process and get a kernel [math]\displaystyle{ K_1 }[/math], resolve it, and so on. When we do, we get an [math]\displaystyle{ E_1 }[/math]-page which looks like

[math]\displaystyle{ E_1^{s,t} = \begin{array}{c|ccc} \vdots & \vdots & \vdots & \vdots\\ 4 & Sq^4\iota, Sq^{3,1}\iota & Sq^{2,1}\alpha_1, Sq^{3}\alpha_1, Sq^2\alpha_2, \alpha_4 & Sq^2\beta_2 & \cdots \\ 3 & Sq^3\iota, Sq^{2,1}\iota &Sq^2\alpha_1, Sq^1\alpha_2 & Sq^1\beta_2& \cdots \\ 2 & Sq^2\iota & \alpha_2, Sq^1\alpha_1 & \beta_2 & \cdots \\ 1 & Sq^1\iota & \alpha_1 & 0 & \cdots \\ 0 & \iota & 0 & 0 & \cdots \\ \hline & 0 & 1 & 2 \end{array} }[/math]

which can be expanded by computer up to degree [math]\displaystyle{ 100 }[/math] with relative ease. Using the found generators and relations, we can calculate the [math]\displaystyle{ E_2 }[/math]-page with relative ease. Sometimes homotopy theorists like to rearrange these elements by having the horizontal index denote [math]\displaystyle{ s }[/math] and the vertical index denote [math]\displaystyle{ t - s }[/math] giving a different type of diagram for the [math]\displaystyle{ E_2 }[/math]-page^{pg 21}. See the diagram above for more information.

Generalizations

The Adams–Novikov spectral sequence is a generalization of the Adams spectral sequence introduced by (Novikov 1967) where ordinary cohomology is replaced by a generalized cohomology theory, often complex bordism or Brown–Peterson cohomology. This requires knowledge of the algebra of stable cohomology operations for the cohomology theory in question, but enables calculations which are completely intractable with the classical Adams spectral sequence.

See also

• Postnikov system
• Steenrod algebra
• Spectrum (topology)
• Adams resolution
• Ravenel's conjectures

References

• Adams, J. Frank (1958), "On the structure and applications of the Steenrod algebra", Commentarii Mathematici Helvetici 32 (1): 180–214, doi:10.1007/BF02564578, ISSN 0010-2571 
• Adams, J. Frank (2013), Stable homotopy theory, Lecture Notes in Mathematics, 3, Springer, ISBN 9783662159422, https://books.google.com/books?id=-vHtCAAAQBAJ 
• Botvinnik, Boris (1992), Manifolds with Singularities and the Adams–Novikov Spectral Sequence, London Mathematical Society Lecture Note Series, Cambridge University Press, ISBN 0-521-42608-1, https://books.google.com/books?id=a3AFRbZ1JnIC 
• McCleary, John (February 2001), A User's Guide to Spectral Sequences, Cambridge Studies in Advanced Mathematics, 58 (2nd ed.), Cambridge University Press, ISBN 978-0-521-56759-6 
• Novikov, Sergei (1967), "Methods of algebraic topology from the point of view of cobordism theory" (in Russian), Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya 31: 855–951 
• Ravenel, Douglas C. (1978), "A novice's guide to the Adams–Novikov spectral sequence", in Barratt, M. G.; Mahowald, Mark E., Geometric applications of homotopy theory (Proc. Conf., Evanston, Ill., 1977), II, Lecture Notes in Mathematics, 658, Springer, pp. 404–475, doi:10.1007/BFb0068728, ISBN 978-3-540-08859-2 
• Ravenel, Douglas C. (2003), Complex cobordism and stable homotopy groups of spheres (2nd ed.), AMS Chelsea, ISBN 978-0-8218-2967-7, http://www.math.rochester.edu/people/faculty/doug/mu.html .

Overviews of computations

• Isaksen, D.C.; Wang, G.; Xu, Z. (2020). "More stable stems". arXiv:2001.04511 [math.AT]. – computes all Adams spectral sequences for the stable homotopy groups of spheres up to degree 90

Higher-order terms

• Baues, H.J.; Jibladze, M. (2004). "Computation of the E_3-term of the Adams spectral sequence". arXiv:math/0407045.
• Baues, H.J.; Blanc, D. (2015). "Higher order derived functors and the Adams spectral sequence". Journal of Pure and Applied Algebra 219 (2): 199–239. doi:10.1016/j.jpaa.2014.04.018. 
• Baues, H.J.; Frankland, M. (2016). "2-track algebras and the Adams spectral sequence". J. Homotopy Relat. Struct. 11 (4): 679–713. doi:10.1007/s40062-016-0147-x. 

External links

• Bruner, Robert R. (June 2, 2009), An Adams Spectral Sequence Primer, http://www.uio.no/studier/emner/matnat/math/MAT9580/v12/undervisningsmateriale/bruner-primer-2009.pdf 
• Hatcher, Allen, "The Adams Spectral Sequence", Spectral Sequences, http://www.math.cornell.edu/~hatcher/SSAT/SSch2.pdf