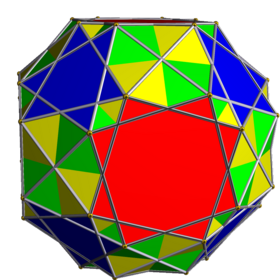
Compound of two snub cubes
| Compound of two snub cubes | |
|---|---|
| |
| Type | Uniform compound |
| Index | UC68 |
| Schläfli symbol | βr{4,3} |
| Coxeter diagram | |
| Polyhedra | 2 snub cubes |
| Faces | 16+48 triangles 12 squares |
| Edges | 120 |
| Vertices | 48 |
| Symmetry group | octahedral (Oh) |
| Subgroup restricting to one constituent | chiral octahedral (O) |
This uniform polyhedron compound is a composition of the 2 enantiomers of the snub cube. As a holosnub, it is represented by Schläfli symbol βr{4,3} and Coxeter diagram ![]()
![]()
![]()
![]()
![]() .
.
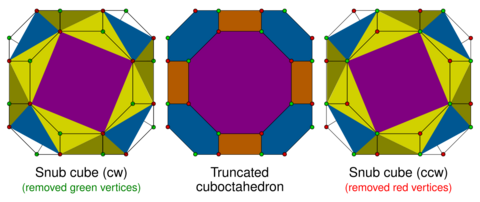
The vertex arrangement of this compound is shared by a convex nonuniform truncated cuboctahedron, having rectangular faces, alongside irregular hexagons and octagons, each alternating with two edge lengths.
Together with its convex hull, it represents the snub cube-first projection of the nonuniform snub cubic antiprism.
Cartesian coordinates
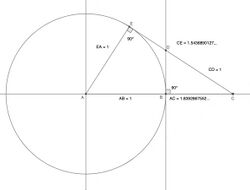
Cartesian coordinates for the vertices are all the permutations of
- (±1, ±ξ, ±1/ξ)
where ξ is the real solution to
- [math]\displaystyle{ \xi^3+\xi^2+\xi=1, \, }[/math]
which can be written
- [math]\displaystyle{ \xi = \frac{1}{3}\left(\sqrt[3]{17+3\sqrt{33}} - \sqrt[3]{-17+3\sqrt{33}} - 1\right) }[/math]
or approximately 0.543689. ξ is the reciprocal of the tribonacci constant.
Equally, the tribonacci constant, t, just like the snub cube, can compute the coordinates as:
- (±1, ±t, ±1/t)
Truncated cuboctahedron
This compound can be seen as the union of the two chiral alternations of a truncated cuboctahedron:
See also
References
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society 79: 447–457, doi:10.1017/S0305004100052440.
 |