Subgroup

Short description: Subset of a group that forms a group itself

In group theory, a branch of mathematics, given a group $G$ under a binary operation ∗, a subset $H$ of $G$ is called a subgroup of $G$ if $H$ also forms a group under the operation ∗. More precisely, $H$ is a subgroup of $G$ if the restriction of ∗ to $H \times H$ is a group operation on $H$ . This is often denoted $H \leq G$ , read as " $H$ is a subgroup of $G$ ".

The trivial subgroup of any group is the subgroup {e} consisting of just the identity element.^[1]

A proper subgroup of a group $G$ is a subgroup $H$ which is a proper subset of $G$ (that is, $H \neq G$ ). This is often represented notationally by $H < G$ , read as " $H$ is a proper subgroup of $G$ ". Some authors also exclude the trivial group from being proper (that is, $H \neq {e$ }).^[2]^[3]

If $H$ is a subgroup of $G$ , then $G$ is sometimes called an overgroup of $H$ .

The same definitions apply more generally when $G$ is an arbitrary semigroup, but this article will only deal with subgroups of groups.

Subgroup tests

Suppose that $G$ is a group, and $H$ is a subset of $G$ . For now, assume that the group operation of $G$ is written multiplicatively, denoted by juxtaposition.

Then $H$ is a subgroup of $G$ if and only if $H$ is nonempty and closed under products and inverses. Closed under products means that for every $a$ and $b$ in $H$ , the product $ab$ is in $H$ . Closed under inverses means that for every $a$ in $H$ , the inverse $a -1$ is in $H$ . These two conditions can be combined into one, that for every $a$ and $b$ in $H$ , the element $ab -1$ is in $H$ , but it is more natural and usually just as easy to test the two closure conditions separately.^[4]
When $H$ is finite, the test can be simplified: $H$ is a subgroup if and only if it is nonempty and closed under products. These conditions alone imply that every element $a$ of $H$ generates a finite cyclic subgroup of $H$ , say of order $n$ , and then the inverse of $a$ is $a n -1$ .^[4]

If the group operation is instead denoted by addition, then closed under products should be replaced by closed under addition, which is the condition that for every $a$ and $b$ in $H$ , the sum $a + b$ is in $H$ , and closed under inverses should be edited to say that for every $a$ in $H$ , the inverse $- a$ is in $H$ .

Basic properties of subgroups

The identity of a subgroup is the identity of the group: if $G$ is a group with identity $e G$ , and $H$ is a subgroup of $G$ with identity $e H$ , then $e H = e G$ .
The inverse of an element in a subgroup is the inverse of the element in the group: if $H$ is a subgroup of a group $G$ , and $a$ and $b$ are elements of $H$ such that $ab = ba = e H$ , then $ab = ba = e G$ .
If $H$ is a subgroup of $G$ , then the inclusion map $H \to G$ sending each element $a$ of $H$ to itself is a homomorphism.
The intersection of subgroups $A$ and $B$ of $G$ is again a subgroup of $G$ .^[5] For example, the intersection of the $x$ -axis and $y$ -axis in [math]\displaystyle{ \R^2 }[/math] under addition is the trivial subgroup. More generally, the intersection of an arbitrary collection of subgroups of $G$ is a subgroup of $G$ .
The union of subgroups $A$ and $B$ is a subgroup if and only if $A \subseteq B$ or $B \subseteq A$ . A non-example: [math]\displaystyle{ 2\Z \cup 3\Z }[/math] is not a subgroup of [math]\displaystyle{ \Z, }[/math] because 2 and 3 are elements of this subset whose sum, 5, is not in the subset. Similarly, the union of the $x$ -axis and the $y$ -axis in [math]\displaystyle{ \R^2 }[/math] is not a subgroup of [math]\displaystyle{ \R^2. }[/math]
If $S$ is a subset of $G$ , then there exists a smallest subgroup containing $S$ , namely the intersection of all of subgroups containing $S$ ; it is denoted by $⟨ S ⟩$ and is called the subgroup generated by $S$ . An element of $G$ is in $⟨ S ⟩$ if and only if it is a finite product of elements of $S$ and their inverses, possibly repeated.^[6]
Every element $a$ of a group $G$ generates a cyclic subgroup $⟨ a ⟩$ . If $⟨ a ⟩$ is isomorphic to [math]\displaystyle{ \Z/n\Z }[/math] (the integers $mod n$ ) for some positive integer $n$ , then $n$ is the smallest positive integer for which $a n = e$ , and $n$ is called the order of $a$ . If $⟨ a ⟩$ is isomorphic to [math]\displaystyle{ \Z, }[/math] then $a$ is said to have infinite order.
The subgroups of any given group form a complete lattice under inclusion, called the lattice of subgroups. (While the infimum here is the usual set-theoretic intersection, the supremum of a set of subgroups is the subgroup generated by the set-theoretic union of the subgroups, not the set-theoretic union itself.) If $e$ is the identity of $G$ , then the trivial group ${e}$ is the minimum subgroup of $G$ , while the maximum subgroup is the group $G$ itself.

G

is the group [math]\displaystyle{ \Z/8\Z, }[/math] the integers mod 8 under addition. The subgroup

H

contains only 0 and 4, and is isomorphic to [math]\displaystyle{ \Z/2\Z. }[/math] There are four left cosets of

H

:

H

itself,

1 + H

,

2 + H

, and

3 + H

(written using additive notation since this is an additive group). Together they partition the entire group

G

into equal-size, non-overlapping sets. The index

[G : H]

is 4.

Cosets and Lagrange's theorem

Main pages: Coset and Lagrange's theorem (group theory)

Given a subgroup $H$ and some $a$ in $G$ , we define the left coset $aH = {ah : h in H}.$ Because $a$ is invertible, the map $φ : H \to aH$ given by $φ(h) = ah$ is a bijection. Furthermore, every element of $G$ is contained in precisely one left coset of $H$ ; the left cosets are the equivalence classes corresponding to the equivalence relation $a 1 ~ a 2$ if and only if [math]\displaystyle{ a_1^{-1}a_2 }[/math] is in $H$ . The number of left cosets of $H$ is called the index of $H$ in $G$ and is denoted by $[G : H]$ .

Lagrange's theorem states that for a finite group $G$ and a subgroup $H$ ,

[math]\displaystyle{ [ G : H ] = { |G| \over |H| } }[/math]

where $| G |$ and $| H |$ denote the orders of $G$ and $H$ , respectively. In particular, the order of every subgroup of $G$ (and the order of every element of $G$ ) must be a divisor of $| G |$ .^[7]^[8]

Right cosets are defined analogously: $Ha = {ha : h in H}.$ They are also the equivalence classes for a suitable equivalence relation and their number is equal to $[G : H]$ .

If $aH = Ha$ for every $a$ in $G$ , then $H$ is said to be a normal subgroup. Every subgroup of index 2 is normal: the left cosets, and also the right cosets, are simply the subgroup and its complement. More generally, if $p$ is the lowest prime dividing the order of a finite group $G$ , then any subgroup of index $p$ (if such exists) is normal.

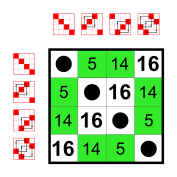
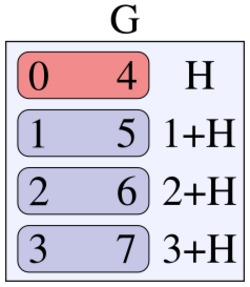
Example: Subgroups of Z₈

Let $G$ be the cyclic group $Z 8$ whose elements are

[math]\displaystyle{ G = \left\{0, 4, 2, 6, 1, 5, 3, 7\right\} }[/math]

and whose group operation is addition modulo 8. Its Cayley table is

+	0	4	2	6	1	5	3	7
0	0	4	2	6	1	5	3	7
4	4	0	6	2	5	1	7	3
2	2	6	4	0	3	7	5	1
6	6	2	0	4	7	3	1	5
1	1	5	3	7	2	6	4	0
5	5	1	7	3	6	2	0	4
3	3	7	5	1	4	0	6	2
7	7	3	1	5	0	4	2	6

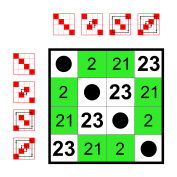
This group has two nontrivial subgroups: $■ J = {0, 4}$ and $■ H = {0, 4, 2, 6}$ , where $J$ is also a subgroup of $H$ . The Cayley table for $H$ is the top-left quadrant of the Cayley table for $G$ ; The Cayley table for $J$ is the top-left quadrant of the Cayley table for $H$ . The group $G$ is cyclic, and so are its subgroups. In general, subgroups of cyclic groups are also cyclic.^[9]

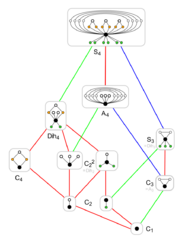
Example: Subgroups of S₄

$S 4$ is the symmetric group whose elements correspond to the permutations of 4 elements.
Below are all its subgroups, ordered by cardinality.
Each group (except those of cardinality 1 and 2) is represented by its Cayley table.

24 elements

Like each group, $S 4$ is a subgroup of itself.

Symmetric group

S 4

All 30 subgroups

Simplified

Hasse diagrams of the lattice of subgroups of

S 4

12 elements

The alternating group contains only the even permutations.
It is one of the two nontrivial proper normal subgroups of $S 4$ . (The other one is its Klein subgroup.)

Alternating group

A 4

Subgroups:
70px
60px60px 60px 60px

8 elements

Dihedral group of order 8

Subgroups:
70px70px70px

233px|Dihedral group of order 8

Subgroups:

6 elements

Symmetric group

S 3

Subgroup:60px

187px|Symmetric group

S 3

Subgroup:

187px|Symmetric group

S 3

Subgroup:

187px|Symmetric group

S 3

Subgroup:

4 elements

Klein four-group

142px|Klein four-group

142px|Klein four-group
(normal subgroup)

Cyclic group

Z 4

142px|Cyclic group

Z 4

Cyclic group

Z 4

3 elements

Cyclic group

Z 3

120px|Cyclic group

Z 3

Cyclic group

Z 3

Cyclic group

Z 3

2 elements

Each permutation $p$ of order 2 generates a subgroup ${1, p$ }. These are the permutations that have only 2-cycles:

There are the 6 transpositions with one 2-cycle. (green background)
And 3 permutations with two 2-cycles. (white background, bold numbers)

1 element

The trivial subgroup is the unique subgroup of order 1.

Other examples

The even integers form a subgroup [math]\displaystyle{ 2\Z }[/math] of the integer ring [math]\displaystyle{ \Z: }[/math] the sum of two even integers is even, and the negative of an even integer is even.
An ideal in a ring $R$ is a subgroup of the additive group of $R$ .
A linear subspace of a vector space is a subgroup of the additive group of vectors.
In an abelian group, the elements of finite order form a subgroup called the torsion subgroup.

Notes

↑ Gallian 2013, p. 61.
↑ Hungerford 1974, p. 32.
↑ Artin 2011, p. 43.
↑ ^4.0 ^4.1 Kurzweil & Stellmacher 1998, p. 4.
↑ Jacobson 2009, p. 41.
↑ Ash 2002.
↑ See a didactic proof in this video.
↑ Dummit & Foote 2004, p. 90.
↑ Gallian 2013, p. 81.

References

Jacobson, Nathan (2009), Basic algebra, 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1 .
Hungerford, Thomas (1974), Algebra (1st ed.), Springer-Verlag, ISBN 9780387905181 .
Artin, Michael (2011), Algebra (2nd ed.), Prentice Hall, ISBN 9780132413770 .
Dummit, David S.; Foote, Richard M. (2004). Abstract algebra (3rd ed.). Hoboken, NJ: Wiley. ISBN 9780471452348. OCLC 248917264.
Gallian, Joseph A. (2013). Contemporary abstract algebra (8th ed.). Boston, MA: Brooks/Cole Cengage Learning. ISBN 978-1-133-59970-8. OCLC 807255720. https://www.worldcat.org/oclc/807255720.
Kurzweil, Hans; Stellmacher, Bernd (1998). Theorie der endlichen Gruppen. Springer-Lehrbuch. doi:10.1007/978-3-642-58816-7. http://dx.doi.org/10.1007/978-3-642-58816-7.
Ash, Robert B. (2002) (in en). Abstract Algebra: The Basic Graduate Year. Department of Mathematics University of Illinois. https://faculty.math.illinois.edu/~r-ash/Algebra.html.

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Subgroup. Read more

[FOOTNOTEGallian201361-1] Gallian 2013, p. 61.

[FOOTNOTEHungerford197432-2] Hungerford 1974, p. 32.

[FOOTNOTEArtin201143-3] Artin 2011, p. 43.

[FOOTNOTEKurzweilStellmacher19984-4] 4.0 ^4.1 Kurzweil & Stellmacher 1998, p. 4.

[FOOTNOTEJacobson200941-5] Jacobson 2009, p. 41.

[FOOTNOTEAsh2002-6] Ash 2002.

[7] See a didactic proof in this video.

[FOOTNOTEDummitFoote200490-8] Dummit & Foote 2004, p. 90.

[FOOTNOTEGallian201381-9] Gallian 2013, p. 81.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

v t e Groups
Basic notions	Subgroup Normal subgroup Commutator subgroup Quotient group Group homomorphism (Semi-) direct product direct sum
Types of groups	Finite groups Abelian groups Cyclic groups Infinite group Simple groups Solvable groups Symmetry group Space group Point group Wallpaper group Trivial group
Discrete groups	Classification of finite simple groups Cyclic group Z_n Alternating group A_n Sporadic groups Mathieu group M_11..12,M_22..24 Conway group Co_1..3 Janko groups J₁, J₂, J₃, J₄ Fischer group F_22..24 Baby monster group B Monster group M Other finite groups Symmetric group S_n Dihedral group D_n Rubik's Cube group
Lie groups	General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) Exceptional Lie groups G₂ F₄ E₆ E₇ E₈ Circle group Lorentz group Poincaré group Quaternion group
Infinite dimensional groups	Conformal group Diffeomorphism group Loop group Quantum group O(∞) SU(∞) Sp(∞)
History Applications Abstract algebra

Anonymous

Search

Subgroup

Namespaces

More

Page actions

Contents

Subgroup tests

Basic properties of subgroups

Cosets and Lagrange's theorem

Example: Subgroups of Z₈