Estermann measure
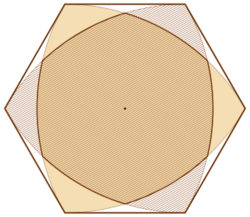
In plane geometry the Estermann measure is a number defined for any bounded convex set describing how close to being centrally symmetric it is. It is the ratio of areas between the given set and its smallest centrally symmetric convex superset. It is one for a set that is centrally symmetric, and less than one for sets whose closure is not centrally symmetric. It is invariant under affine transformations of the plane.[1]
Properties
If [math]\displaystyle{ c }[/math] is the center of symmetry of the smallest centrally-symmetric set containing a given convex body [math]\displaystyle{ K }[/math], then the centrally-symmetric set itself is the convex hull of the union of [math]\displaystyle{ K }[/math] with its reflection across [math]\displaystyle{ c }[/math].[1]
Minimizers
The shapes of minimum Estermann measure are the triangles, for which this measure is 1/2.[1][2] The curve of constant width with the smallest possible Estermann measure is the Reuleaux triangle.[3]
History
The Estermann measure is named after Theodor Estermann, who first proved in 1928 that this measure is always at least 1/2, and that a convex set with Estermann measure 1/2 must be a triangle.[4][1][2] Subsequent proofs were given by Friedrich Wilhelm Levi, by István Fáry, and by Isaak Yaglom and Vladimir Boltyansky.[1]
See also
- Kovner–Besicovitch measure, a measure of central symmetry defined using subsets in place of supersets
References
- ↑ 1.0 1.1 1.2 1.3 1.4 "Measures of symmetry for convex sets", Convexity, Proceedings of Symposia in Pure Mathematics, 7, Providence, Rhode Island: American Mathematical Society, 1963, pp. 233–270
- ↑ 2.0 2.1 Makeev, V. V. (2007), "Some extremal problems for vector bundles", St. Petersburg Mathematical Journal 19 (2): 131–155, doi:10.1090/S1061-0022-08-00998-9
- ↑ Finch, Steven R. (2003), "8.10 Reuleaux Triangle Constants", Mathematical Constants, Encyclopedia of Mathematics and its Applications, Cambridge University Press, pp. 513–514, ISBN 978-0-521-81805-6, http://www.people.fas.harvard.edu/~sfinch/csolve/rx.pdf.
- ↑ "Über den Vektorenbereich eines konvexen Körpers", Mathematische Zeitschrift 28 (1): 471–475, 1928, doi:10.1007/BF01181177
 |

