Finance:Solvency cone
This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (December 2013) (Learn how and when to remove this template message) |
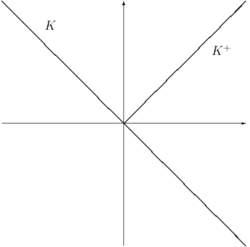
The solvency cone is a concept used in financial mathematics which models the possible trades in the financial market. This is of particular interest to markets with transaction costs. Specifically, it is the convex cone of portfolios that can be exchanged to portfolios of non-negative components (including paying of any transaction costs).
Mathematical basis
If given a bid-ask matrix [math]\displaystyle{ \Pi }[/math] for [math]\displaystyle{ d }[/math] assets such that [math]\displaystyle{ \Pi = \left(\pi^{ij}\right)_{1 \leq i,j \leq d} }[/math] and [math]\displaystyle{ m \leq d }[/math] is the number of assets which with any non-negative quantity of them can be "discarded" (traditionally [math]\displaystyle{ m = d }[/math]), then the solvency cone [math]\displaystyle{ K(\Pi) \subset \mathbb{R}^d }[/math] is the convex cone spanned by the unit vectors [math]\displaystyle{ e^i, 1 \leq i \leq m }[/math] and the vectors [math]\displaystyle{ \pi^{ij}e^i-e^j, 1 \leq i,j \leq d }[/math].[1]
Definition
A solvency cone [math]\displaystyle{ K }[/math] is any closed convex cone such that [math]\displaystyle{ K \subseteq \mathbb{R}^d }[/math] and [math]\displaystyle{ K \supseteq \mathbb{R}^d_+ }[/math].[2]
Uses
A process of (random) solvency cones [math]\displaystyle{ \left\{K_t(\omega)\right\}_{t=0}^T }[/math] is a model of a financial market. This is sometimes called a market process.
The negative of a solvency cone is the set of portfolios that can be obtained starting from the zero portfolio. This is intimately related to self-financing portfolios.[citation needed]
The dual cone of the solvency cone ([math]\displaystyle{ K^+ = \left\{w \in \mathbb{R}^d: \forall v \in K: 0 \leq w^Tv\right\} }[/math]) are the set of prices which would define a friction-less pricing system for the assets that is consistent with the market. This is also called a consistent pricing system.[1][3]
Examples
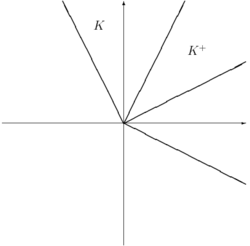
Assume there are 2 assets, A and M with 1 to 1 exchange possible.
Frictionless market
In a frictionless market, we can obviously make (1A,-1M) and (-1A,1M) into non-negative portfolios, therefore [math]\displaystyle{ K = \{x \in \mathbb{R}^2: (1,1)x \geq 0\} }[/math]. Note that (1,1) is the "price vector."
With transaction costs
Assume further that there is 50% transaction costs for each deal. This means that (1A,-1M) and (-1A,1M) cannot be exchanged into non-negative portfolios. But, (2A,-1M) and (-1A,2M) can be traded into non-negative portfolios. It can be seen that [math]\displaystyle{ K = \{x \in \mathbb{R}^2: (2,1)x \geq 0, (1,2)x \geq 0\} }[/math].
The dual cone of prices is thus easiest to see in terms of prices of A in terms of M (and similarly done for price of M in terms of A):
- someone offers 1A for tM: [math]\displaystyle{ (0,t) \rightarrow (1,0) \rightarrow (0,\frac{1}{2}) }[/math] therefore there is arbitrage if [math]\displaystyle{ t \lt \frac{1}{2} }[/math]
- someone offers tM for 1A: [math]\displaystyle{ (1,0) \rightarrow (0,t) \rightarrow (\frac{t}{2},0) }[/math] therefore there is arbitrage if [math]\displaystyle{ t \gt 2 }[/math]
Properties
If a solvency cone [math]\displaystyle{ K }[/math]:
- contains a line, then there is an exchange possible without transaction costs.
- [math]\displaystyle{ K = \mathbb{R}^d_+ }[/math], then there is no possible exchange, i.e. the market is completely illiquid.
References
- ↑ 1.0 1.1 Schachermayer, Walter (November 15, 2002). The Fundamental Theorem of Asset Pricing under Proportional Transaction Costs in Finite Discrete Time.
- ↑ Hamel, A. H.; Heyde, F. (2010). "Duality for Set-Valued Measures of Risk". SIAM Journal on Financial Mathematics 1 (1): 66–95. doi:10.1137/080743494.
- ↑ Löhne, Andreas; Rudloff, Birgit (2015). "On the dual of the solvency cone". Discrete Applied Mathematics 186: 176–185. doi:10.1016/j.dam.2015.01.030. ISSN 0166-218X.
 |