Physics:White's illusion
White's illusion is a brightness illusion in which certain stripes of a black-and-white grating are replaced by gray rectangles (see the figure). Both of the gray bars of A and B have the same color, luminance, and opacity. The brightness of the gray rectangles appears to be closer to the brightness of the top and bottom bordering stripes. This is opposite to any explanation based on lateral inhibition; hence it cannot explain the illusion.[1] A similar illusion occurs when the horizontal stripes have different colors; this is known as the Munker–White illusion or the Munker illusion, based on the Bezold effect.[2][3]
Lateral inhibition
The amount of each bipolar cell response depends on the amount of the stimulation it receives from the receptor and the amount that this response is decreased by the lateral inhibition it receives from its neighboring cells.[4]
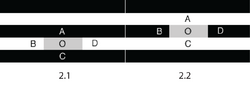
Lateral inhibition cannot explain White's illusion.[1][better source needed] In Figure 2.1 lateral inhibition sent by black cells A and C should make cell O lighter; in Figure 2.2 lateral inhibition sent by white cells A and C should make cell O darker. It is suggested that brightness induction follows the brightness contrast in the direction of the bar not the surrounding area.
Lateral inhibition explained
In Figure 2.1 we assume that light dropping on cells B and D generates a response of 100 units. Since the points A and C are darker we assume that only 20 units are generated from these points. Another assumption is that the lateral inhibition sent by each cell is 10% of its response; cells B and D send an inhibition of 10 units each and cells A and C send an inhibition of 2 units each. The inhibition sent by cells A and C is larger since their size is bigger than the size of cells B and D (let's say 2 times). This concludes that cell O receives an inhibition I = 10 + 10 + 2 × 2 + 2 × 2 = 28.
In Figure 2.2 with the same assumptions as above stated, cell O receives an inhibition of I = 10 × 2 + 10 × 2 + 2 + 2 = 44.
Because point O in Figure 2.1 receives an inhibition smaller than the point O in Figure 2.2 the gray cell should be lighter.
Experiments on lateral inhibition
White and White (1985) concluded that at a higher spatial frequency the grating of White's illusion could be described by brightness assimilation. They also concluded that at lower spatial frequencies White's illusion is still present.[citation needed]
Blakeslee and McCourt (2004) suggested that patterns whose scales are larger compared to the encoding filters (low spatial frequency) are represented with a loss of low frequency information exhibiting brightness contrast; patterns whose scales are smaller compared to encoding filters (high spatial frequency), are represented with a loss of high frequency information exhibiting brightness assimilation.[5]
Belongingness
Our perception of an area's lightness is influenced by the part of the surroundings to which the area appears to belong.
A disc example consists of four discs on the left which are identical to four discs on the right in terms of how much light is reflected from the discs, that is to say, they are physically identical. The theory to explain the different psychological experiences is called belongingness.
The discs on the left appear dark and the ones on the right appear light, this is because of the two displays. In the display on the left, the dark area on the left seemingly belongs to the discs, and the discs are obscured by the light mist. On the right side, the same dark areas are interpreted as belonging to the dark mist. In the meanwhile, the white parts are seen as the color of the discs. Therefore, our perception of the lightness of the discs is significantly influenced by the display, which is the mist in this case (Anderson & Winawer, 2005).
The belongingness theory has been suggested as an explanation of White's illusion. According to belongingness theory, the lightness of rectangle A is influenced by the white display, which should be the white bars that surround it. Similarly, the rectangle B on the right side is surrounded by the dark bars, and the lightness of rectangle B is affected by the dark background. As a result, area A which rests on the white background appears darker than area B which rests on the dark background.[6]
Belongingness theory only explains why rectangle A looks darker than rectangle B and does not discuss why the gray area on rectangle A looks darker than in rectangle B; secondly, when talking about the background, Belongingness theory appears quite the same as simultaneous contrast theory, they just use different names.[1] Kelly and Grossberg (2000, P&P, 62, 1596-1619) explain and simulate these perceived differences and various other surface brightness and figure-ground percepts, such as those arising from Bregman-Kanizsa, Benary cross, and checkerboard displays, using the FACADE theory of 3-D vision and figure-ground perception.
See also
References
- ↑ 1.0 1.1 1.2 Anderson, L. Barton (2003). "Perceptual organization and White's Illusion". Perception 32 (3): 269–284. doi:10.1068/p3216. PMID 12729379. http://www.psych.usyd.edu.au/staff/barta/lab/TexturedWhites.pdf. Retrieved 2016-07-18.
- ↑ Bach, Michael. "Munker Illusion". http://www.michaelbach.de/ot/col_Munker/index.html.
- ↑ Bach, Michael. "Munker-White Illusion". http://www.michaelbach.de/ot/lum-white/index.html.
- ↑ Sensation and perception, E. Bruce Goldstein, Edition 8, illustrated, Publisher Cengage Learning, 2009
- ↑ Blakeslee, Barbara; McCourt, Mark E. (1999). "A multiscale spatial filtering account of the White effect, simultaneous brightness contrast and grating induction". Vision Research 39 (26): 4361–4377. doi:10.1016/s0042-6989(99)00119-4. PMID 10789430. http://cseweb.ucsd.edu/~gary/cs200/w04/papers/blakeslee-99.pdf. Retrieved 9 October 2014.
- ↑ Gilchrist, A (1999). "An Anchoring Theory of Lightness Perception". Psychological Review 106 (4): 795–834. doi:10.1037/0033-295x.106.4.795. PMID 10560329. http://wexler.free.fr/library/files/gilchrist%20(1999)%20an%20anchoring%20theory%20of%20lightness%20perception.pdf. Retrieved 9 October 2014.
External links
- "These skulls look purple and orange. They are both red", by Nicole Wetsman, December 18, 2018, Popular Science magazine
- The Early History of White's Illusion, Michael White, Colour: Design & Creativity (5) (2010): 7, 1–7, 2010
 |