Triangle wave
Template:Infobox mathematical function
A triangular wave or triangle wave is a non-sinusoidal waveform named for its triangular shape. It is a periodic, piecewise linear, continuous real function.
Like a square wave, the triangle wave contains only odd harmonics. However, the higher harmonics roll off much faster than in a square wave (proportional to the inverse square of the harmonic number as opposed to just the inverse).
Definitions
Definition
A triangle wave of period p that spans the range [0,1] is defined as: [math]\displaystyle{ x(t)= 2 \left| \frac{t}{p} - \left \lfloor \frac{t}{p} + \frac{1}{2} \right \rfloor \right| }[/math] where [math]\displaystyle{ \lfloor\,\ \rfloor }[/math] is the floor function. This can be seen to be the absolute value of a shifted sawtooth wave.
For a triangle wave spanning the range [−1,1] the expression becomes: [math]\displaystyle{ x(t)= 2 \left | 2 \left ( \frac{t}{p} - \left \lfloor {t \over p} + {1 \over 2} \right \rfloor \right) \right | - 1. }[/math]
A more general equation for a triangle wave with amplitude [math]\displaystyle{ a }[/math] and period [math]\displaystyle{ p }[/math] using the modulo operation and absolute value is:
[math]\displaystyle{ y(x) = \frac{4a}{p} \left| \left( \left(x - \frac{p}{4}\right) \bmod p \right) - \frac{p}{2} \right| - a. }[/math]
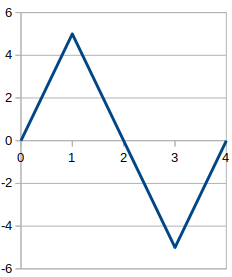
For example, for a triangle wave with amplitude 5 and period 4: [math]\displaystyle{ y(x) = 5 \left | \bigl( (x - 1) \bmod 4 \bigr) - 2 \right | - 5. }[/math]
A phase shift can be obtained by altering the value of the [math]\displaystyle{ - p/4 }[/math] term, and the vertical offset can be adjusted by altering the value of the [math]\displaystyle{ - a }[/math] term.
As this only uses the modulo operation and absolute value, it can be used to simply implement a triangle wave on hardware electronics.
Note that in many programming languages, the % operator is a remainder operator (with result the same sign as the dividend), not a modulo operator; the modulo operation can be obtained by using ((x % p) + p) % p in place of x % p. In e.g. JavaScript, this results in an equation of the form 4*a/p * Math.abs((((x-p/4)%p)+p)%p - p/2) - a.
Relation to the square wave
The triangle wave can also be expressed as the integral of the square wave: [math]\displaystyle{ x(t) = \int_0^t \sgn\left(\sin\frac{u}{p}\right)\,du. }[/math]
Expression in trigonometric functions
A triangle wave with period p and amplitude a can be expressed in terms of sine and arcsine (whose value ranges from −π/2 to π/2): [math]\displaystyle{ y(x) = \frac{2a}{\pi} \arcsin\left(\sin\left(\frac{2\pi}{p}x\right)\right). }[/math] The identity [math]\displaystyle{ \cos{x} = \sin\left(\frac{p}{4}-x\right) }[/math] can be used to convert from a triangle "sine" wave to a triangular "cosine" wave. This phase-shifted triangle wave can also be expressed with cosine and arccosine: [math]\displaystyle{ y(x) = a - \frac{2a}{\pi} \arccos\left(\cos\left(\frac{2\pi}{p}x\right)\right). }[/math]
Expressed as alternating linear functions
Another definition of the triangle wave, with range from −1 to 1 and period p, is: [math]\displaystyle{ x(t) = \frac{4}{p} \left (t-\frac{p}{2} \left \lfloor\frac{2 t}{p}+\frac{1}{2} \right \rfloor \right )(-1)^\left \lfloor\frac{2 t}{p} + \frac{1}{2} \right \rfloor }[/math]
Harmonics
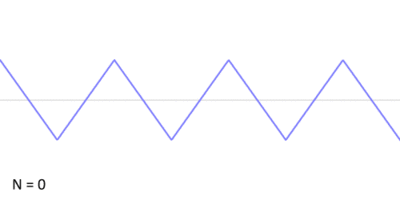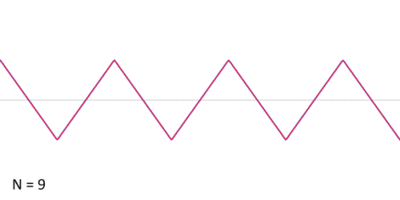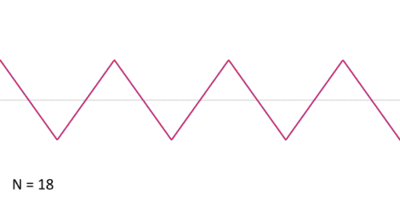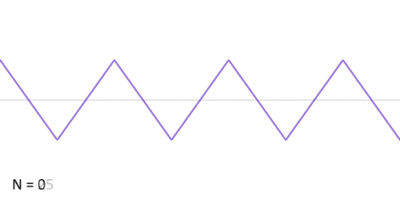
It is possible to approximate a triangle wave with additive synthesis by summing odd harmonics of the fundamental while multiplying every other odd harmonic by −1 (or, equivalently, changing its phase by π) and multiplying the amplitude of the harmonics by one over the square of their mode number, n (which is equivalent to one over the square of their relative frequency to the fundamental).
The above can be summarised mathematically as follows: [math]\displaystyle{ \begin{align} x_\mathrm{triangle}(t) & {} = \frac8{\pi^2}\sum_{i=0}^{N - 1} (-1)^i n^{-2} \sin\left(2\pi f_0 n t\right) \end{align} }[/math] where N is the number of harmonics to include in the approximation, t is the independent variable (e.g. time for sound waves), [math]\displaystyle{ f_0 }[/math] is the fundamental frequency, and i is the harmonic label which is related to its mode number by [math]\displaystyle{ n = 2i + 1 }[/math].
This infinite Fourier series converges quickly to the triangle wave as N tends to infinity, as shown in the animation.
Arc length
The arc length per period for a triangle wave, denoted by s, is given in terms of the amplitude a and period length p by [math]\displaystyle{ s = \sqrt{(4a)^2 + p^2}. }[/math]
See also
- List of periodic functions
- Sine wave
- Square wave
- Sawtooth wave
- Pulse wave
- Sound
- Triangle function
- Wave
- Zigzag
References
- Weisstein, Eric W.. "Fourier Series - Triangle Wave". http://mathworld.wolfram.com/FourierSeriesTriangleWave.html.
 |