Addition principle

Short description: Counting principle in combinatorics

5+0=5 illustrated with collections of dots.

In combinatorics, the addition principle or rule of sum is a basic counting principle. Stated simply, it is the intuitive idea that if we have A number of ways of doing something and B number of ways of doing another thing and we can not do both at the same time, then there are [math]\displaystyle{ A + B }[/math] ways to choose one of the actions. In mathematical terms, the addition principle states that, for disjoint sets A and B, we have [math]\displaystyle{ |A\cup B| = |A| + |B| }[/math].

The rule of sum is a fact about set theory.

The addition principle can be extended to several sets. If [math]\displaystyle{ S_1, S_2,\ldots, S_n }[/math] are pairwise disjoint sets, then we have:[math]\displaystyle{ |S_1|+|S_2|+\cdots+|S_{n}| = |S_1 \cup S_2 \cup \cdots \cup S_n|. }[/math]This statement can be proven from the addition principle by induction on n.

Simple example

3+2=5 illustrated with shapes.

A person has decided to shop at one store today, either in the north part of town or the south part of town. If they visit the north part of town, they will shop at either a mall, a furniture store, or a jewelry store (3 ways). If they visit the south part of town then they will shop at either a clothing store or a shoe store (2 ways).

Thus there are [math]\displaystyle{ 3 + 2 = 5 }[/math] possible shops the person could end up shopping at today.

Inclusion–exclusion principle

A series of Venn diagrams illustrating the principle of inclusion-exclusion.

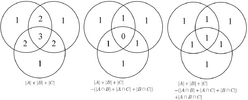
The inclusion–exclusion principle (also known as the sieve principle) can be thought of as a generalization of the rule of sum in that it too enumerates the number of elements in the union of some sets (but does not require the sets to be disjoint). It states that if A₁, ..., A_n are finite sets, then [math]\displaystyle{ \left|\bigcup_{i=1}^n A_i\right| =\sum_{i=1}^n\left|A_i\right| -\sum_{i,j\,:\,1 \le i \lt j \le n}\left|A_i\cap A_j\right| + \sum_{i,j,k\,:\,1 \le i \lt j \lt k \le n}\left|A_i\cap A_j\cap A_k\right|-\ \cdots\ + (-1)^{n-1} \left|A_1\cap\cdots\cap A_n\right|. }[/math]

Subtraction principle

Similarly, for a given finite set S, and given another set A, if [math]\displaystyle{ A \subset S }[/math], then [math]\displaystyle{ |A^c| = |S| - |A| }[/math]. To prove this, notice that [math]\displaystyle{ |A^c| + |A| = |S| }[/math] by the addition principle.

Applications

The addition principle can be used to prove Pascal's rule combinatorially. To calculate [math]\displaystyle{ \binom{n + 1}{k} }[/math], one can view it as the number of ways to choose k people from a room containing n children and 1 teacher. Then there are [math]\displaystyle{ \binom{n}{k} }[/math] ways to choose people without choosing the teacher, and [math]\displaystyle{ \binom{n}{k-1} }[/math] ways to choose people that includes the teacher. Thus [math]\displaystyle{ \binom{n+1}{k} = \binom{n}{k} + \binom{n}{k-1} }[/math].

The addition principle can also be used to prove the multiplication principle.

References

Bibliography

• Biggs, Norman L. (2002). Discrete Mathematics. India: Oxford University Press. ISBN 978-0-19-871369-2. 

See also

• Combinatorial principle
• Rule of product
• Inclusion–exclusion principle

fi:Todennäköisyysteoria#Tuloperiaate ja summaperiaate