Approximate entropy
In statistics, an approximate entropy (ApEn) is a technique used to quantify the amount of regularity and the unpredictability of fluctuations over time-series data.[1] For example, consider two series of data:
- Series A: (0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, ...), which alternates 0 and 1.
- Series B: (0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, ...), which have either a value of 0 or 1, chosen randomly, each with probability 1/2.
Moment statistics, such as mean and variance, will not distinguish between these two series. Nor will rank order statistics distinguish between these series. Yet series A is perfectly regular: knowing a term has the value of 1 enables one to predict with certainty that the next term will have the value of 0. In contrast, series B is randomly valued: knowing a term has the value of 1 gives no insight into what value the next term will have.
Regularity was originally measured by exact regularity statistics, which has mainly centered on various entropy measures.[1] However, accurate entropy calculation requires vast amounts of data, and the results will be greatly influenced by system noise,[2] therefore it is not practical to apply these methods to experimental data. ApEn was first proposed (under a different name) by Aviad Cohen and Itamar Procaccia,[3] as an approximate algorithm to compute an exact regularity statistic, Kolmogorov–Sinai entropy, and later popularized by Steve M. Pincus. ApEn was initially used to analyze chaotic dynamics and medical data, such as heart rate,[1] and later spread its applications in finance,[4] physiology,[5] human factors engineering,[6] and climate sciences.[7]
Algorithm
A comprehensive step-by-step tutorial with an explanation of the theoretical foundations of Approximate Entropy is available.[8] The algorithm is:
- Step 1
- Assume a time series of data . These are raw data values from measurements equally spaced in time.
- Step 2
- Let be a positive integer, with , which represents the length of a run of data (essentially a window).
Let be a positive real number, which specifies a filtering level.
Let . - Step 3
- Define for each where . In other words, is an -dimensional vector that contains the run of data starting with .
Define the distance between two vectors and as the maximum of the distances between their respective components, given by - for .
- Step 4
- Define a count as
- for each where . Note that since takes on all values between 1 and , the match will be counted when (i.e. when the test subsequence, , is matched against itself, ).
- Step 5
- Define
- where is the natural logarithm, and for a fixed , , and as set in Step 2.
- Step 6
- Define approximate entropy () as
- Parameter selection
- Typically, choose or , whereas depends greatly on the application.
An implementation on Physionet,[9] which is based on Pincus,[2] use instead of in Step 4. While a concern for artificially constructed examples, it is usually not a concern in practice.
Example
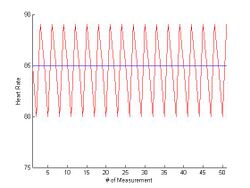
Consider a sequence of samples of heart rate equally spaced in time:
Note the sequence is periodic with a period of 3. Let's choose and (the values of and can be varied without affecting the result).
Form a sequence of vectors:
Distance is calculated repeatedly as follows. In the first calculation,
- which is less than .
In the second calculation, note that , so
- which is greater than .
Similarly,
The result is a total of 17 terms such that . These include . In these cases, is
Note in Step 4, for . So the terms such that include , and the total number is 16.
At the end of these calculations, we have
Then we repeat the above steps for . First form a sequence of vectors:
By calculating distances between vector , we find the vectors satisfying the filtering level have the following characteristic:
Therefore,
At the end of these calculations, we have
Finally,
The value is very small, so it implies the sequence is regular and predictable, which is consistent with the observation.
Python implementation
import math
def approx_entropy(time_series, run_length, filter_level) -> float:
"""
Approximate entropy
>>> import random
>>> regularly = [85, 80, 89] * 17
>>> print(f"{approx_entropy(regularly, 2, 3):e}")
1.099654e-05
>>> randomly = [random.choice([85, 80, 89]) for _ in range(17*3)]
>>> 0.8 < approx_entropy(randomly, 2, 3) < 1
True
"""
def _maxdist(x_i, x_j):
return max(abs(ua - va) for ua, va in zip(x_i, x_j))
def _phi(m):
n = len(time_series) - m + 1
x = [
[time_series[j] for j in range(i, i + m)]
for i in range(n)
]
counts = [
sum(1 for x_j in x if _maxdist(x_i, x_j) <= filter_level) / n for x_i in x
]
return sum(math.log(c) for c in counts) / n
return abs(_phi(run_length + 1) - _phi(run_length))
if __name__ == "__main__":
import doctest
doctest.testmod()
MATLAB implementation
- Fast Approximate Entropy from MatLab Central
- approximateEntropy
Interpretation
The presence of repetitive patterns of fluctuation in a time series renders it more predictable than a time series in which such patterns are absent. ApEn reflects the likelihood that similar patterns of observations will not be followed by additional similar observations.[10] A time series containing many repetitive patterns has a relatively small ApEn; a less predictable process has a higher ApEn.
Advantages
The advantages of ApEn include:[2]
- Lower computational demand. ApEn can be designed to work for small data samples ( points) and can be applied in real time.
- Less effect from noise. If data is noisy, the ApEn measure can be compared to the noise level in the data to determine what quality of true information may be present in the data.
Limitations
The ApEn algorithm counts each sequence as matching itself to avoid the occurrence of in the calculations. This step might introduce bias in ApEn, which causes ApEn to have two poor properties in practice:[11]
- ApEn is heavily dependent on the record length and is uniformly lower than expected for short records.
- It lacks relative consistency. That is, if ApEn of one data set is higher than that of another, it should, but does not, remain higher for all conditions tested.
Applications
ApEn has been applied to classify electroencephalography (EEG) in psychiatric diseases, such as schizophrenia,[12] epilepsy,[13] and addiction.[14]
See also
References
- ↑ 1.0 1.1 1.2 Pincus, S. M.; Gladstone, I. M.; Ehrenkranz, R. A. (1991). "A regularity statistic for medical data analysis". Journal of Clinical Monitoring and Computing 7 (4): 335–345. doi:10.1007/BF01619355. PMID 1744678.
- ↑ 2.0 2.1 2.2 Pincus, S. M. (1991). "Approximate entropy as a measure of system complexity". Proceedings of the National Academy of Sciences 88 (6): 2297–2301. doi:10.1073/pnas.88.6.2297. PMID 11607165. Bibcode: 1991PNAS...88.2297P.
- ↑ Cohen, A.; Procaccia, I. (1985). "Computing the Kolmogorov entropy from time signals of dissipative and conservative dynamical systems". Physical Review A 28 (3): 2591(R). doi:10.1103/PhysRevA.31.1872. PMID 9895695. Bibcode: 1985PhRvA..31.1872C.
- ↑ Pincus, S.M.; Kalman, E.K. (2004). "Irregularity, volatility, risk, and financial market time series". Proceedings of the National Academy of Sciences 101 (38): 13709–13714. doi:10.1073/pnas.0405168101. PMID 15358860. Bibcode: 2004PNAS..10113709P.
- ↑ Pincus, S.M.; Goldberger, A.L. (1994). "Physiological time-series analysis: what does regularity quantify?". The American Journal of Physiology 266 (4): 1643–1656. doi:10.1152/ajpheart.1994.266.4.H1643. PMID 8184944.
- ↑ McKinley, R.A.; McIntire, L.K.; Schmidt, R; Repperger, D.W.; Caldwell, J.A. (2011). "Evaluation of Eye Metrics as a Detector of Fatigue". Human Factors 53 (4): 403–414. doi:10.1177/0018720811411297. PMID 21901937.
- ↑ Delgado-Bonal, Alfonso; Marshak, Alexander; Yang, Yuekui; Holdaway, Daniel (2020-01-22). "Analyzing changes in the complexity of climate in the last four decades using MERRA-2 radiation data". Scientific Reports 10 (1): 922. doi:10.1038/s41598-020-57917-8. ISSN 2045-2322. PMID 31969616. Bibcode: 2020NatSR..10..922D.
- ↑ Delgado-Bonal, Alfonso; Marshak, Alexander (June 2019). "Approximate Entropy and Sample Entropy: A Comprehensive Tutorial" (in en). Entropy 21 (6): 541. doi:10.3390/e21060541. PMID 33267255. Bibcode: 2019Entrp..21..541D.
- ↑ "PhysioNet". http://physionet.org/physiotools/ApEn/.
- ↑ Ho, K. K.; Moody, G. B.; Peng, C.K.; Mietus, J. E.; Larson, M. G.; levy, D; Goldberger, A. L. (1997). "Predicting survival in heart failure case and control subjects by use of fully automated methods for deriving nonlinear and conventional indices of heart rate dynamics". Circulation 96 (3): 842–848. doi:10.1161/01.cir.96.3.842. PMID 9264491.
- ↑ Richman, J.S.; Moorman, J.R. (2000). "Physiological time-series analysis using approximate entropy and sample entropy". American Journal of Physiology. Heart and Circulatory Physiology 278 (6): 2039–2049. doi:10.1152/ajpheart.2000.278.6.H2039. PMID 10843903.
- ↑ Sabeti, Malihe (2009). "Entropy and complexity measures for EEG signal classification of schizophrenic and control participants". Artificial Intelligence in Medicine 47 (3): 263–274. doi:10.1016/j.artmed.2009.03.003. PMID 19403281.
- ↑ Yuan, Qi (2011). "Epileptic EEG classification based on extreme learning machine and nonlinear features". Epilepsy Research 96 (1–2): 29–38. doi:10.1016/j.eplepsyres.2011.04.013. PMID 21616643.
- ↑ Yun, Kyongsik (2012). "Decreased cortical complexity in methamphetamine abusers". Psychiatry Research: Neuroimaging 201 (3): 226–32. doi:10.1016/j.pscychresns.2011.07.009. PMID 22445216.
 |
