Astronomy:Maclaurin spheroid
A Maclaurin spheroid is an oblate spheroid which arises when a self-gravitating fluid body of uniform density rotates with a constant angular velocity. This spheroid is named after the Scottish mathematician Colin Maclaurin, who formulated it for the shape of Earth in 1742.[1] In fact the figure of the Earth is far less oblate than Maclaurin's formula suggests, since the Earth is not homogeneous, but has a dense iron core. The Maclaurin spheroid is considered to be the simplest model of rotating ellipsoidal figures in hydrostatic equilibrium since it assumes uniform density.
Maclaurin formula
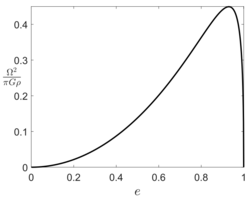
For a spheroid with equatorial semi-major axis [math]\displaystyle{ a }[/math] and polar semi-minor axis [math]\displaystyle{ c }[/math], the angular velocity [math]\displaystyle{ \Omega }[/math] about [math]\displaystyle{ c }[/math] is given by Maclaurin's formula[2]
- [math]\displaystyle{ \frac{\Omega^2}{\pi G\rho} = \frac{2\sqrt{1-e^2}}{e^3}(3-2e^2) \sin^{-1}e - \frac{6}{e^2}(1-e^2), \quad e^2 = 1-\frac{c^2}{a^2}, }[/math]
where [math]\displaystyle{ e }[/math] is the eccentricity of meridional cross-sections of the spheroid, [math]\displaystyle{ \rho }[/math] is the density and [math]\displaystyle{ G }[/math] is the gravitational constant. The formula predicts two possible equilibrium figures when [math]\displaystyle{ \Omega\rightarrow 0 }[/math], one is a sphere ([math]\displaystyle{ e\rightarrow 0 }[/math]) and the other is a very flattened spheroid ([math]\displaystyle{ e\rightarrow 1 }[/math]). The maximum angular velocity occurs at eccentricity [math]\displaystyle{ e=0.92996 }[/math] and its value is [math]\displaystyle{ \Omega^2/(\pi G\rho)=0.449331 }[/math], so that above this speed, no equilibrium figures exist. The angular momentum [math]\displaystyle{ L }[/math] is
- [math]\displaystyle{ \frac{L}{\sqrt{GM^3\bar{a}}} = \frac{\sqrt 3}{5} \left(\frac{a}{\bar{a}}\right)^2 \sqrt{\frac{\Omega^2}{\pi G\rho}} \ , \quad \bar{a} = (a^2c)^{1/3} }[/math]
where [math]\displaystyle{ M }[/math] is the mass of the spheroid and [math]\displaystyle{ \bar{a} }[/math] is the mean radius, the radius of a sphere of the same volume as the spheroid.
Stability
For a Maclaurin spheroid of eccentricity greater than 0.812670,[3] a Jacobi ellipsoid of the same angular momentum has lower total energy. If such a spheroid is composed of a viscous fluid, and if it suffers a perturbation which breaks its rotational symmetry, then it will gradually elongate into the Jacobi ellipsoidal form, while dissipating its excess energy as heat. This is termed secular instability. However, for a similar spheroid composed of an inviscid fluid, the perturbation will merely result in an undamped oscillation. This is described as dynamic (or ordinary) stability.
A Maclaurin spheroid of eccentricity greater than 0.952887[3] is dynamically unstable. Even if it is composed of an inviscid fluid and has no means of losing energy, a suitable perturbation will grow (at least initially) exponentially. Dynamic instability implies secular instability (and secular stability implies dynamic stability).[4]
See also
References
- ↑ Maclaurin, Colin. A Treatise of Fluxions: In Two Books. 1. Vol. 1. Ruddimans, 1742.
- ↑ Chandrasekhar, Subrahmanyan. Ellipsoidal figures of equilibrium. Vol. 10. New Haven: Yale University Press, 1969.
- ↑ 3.0 3.1 Poisson, Eric; Will, Clifford (2014). Gravity: Newtonian, Post-Newtonian, Relativistic. Cambridge University Press. pp. 102–104. ISBN 978-1107032866. https://books.google.com/books?id=lWBzAwAAQBAJ&pg=PA103.
- ↑ Lyttleton, Raymond Arthur (1953). The Stability Of Rotating Liquid Masses. Cambridge University Press. ISBN 9781316529911. https://archive.org/details/stabilityofrotat032172mbp.
 |  |
