Astronomy:Tides in marginal seas

From HandWiki
Short description: Dynamics of tidal wave deformation in the shallow waters of the marginal seas

Tides in marginal seas are tides affected by their location in semi-enclosed areas along the margins of continents and differ from tides in the open oceans. Tides are water level variations caused by the gravitational interaction between the Moon, the Sun and the Earth. The resulting tidal force is a secondary effect of gravity: it is the difference between the actual gravitational force and the centrifugal force. While the centrifugal force is constant across the Earth, the gravitational force is dependent on the distance between the two bodies and is therefore not constant across the Earth. The tidal force is thus the difference between these two forces on each location on the Earth.[1]

In an idealized situation, assuming a planet with no landmasses (an aqua planet), the tidal force would result in two tidal bulges on opposite sides of the earth. This is called the equilibrium tide. However, due to global and local ocean responses different tidal patterns are generated. The complicated ocean responses are the result of the continental barriers, resonance due to the shape of the ocean basin, the tidal waves impossibility to keep up with the Moons tracking, the Coriolis acceleration and the elastic response of the solid earth.[2]

In addition, when the tide arrives in the shallow seas it interacts with the sea floor which leads to the deformation of the tidal wave. As a results, tides in shallow waters tend to be larger, of shorter wavelength, and possibly nonlinear relative to tides in the deep ocean.[3]

Tides on the continental shelf

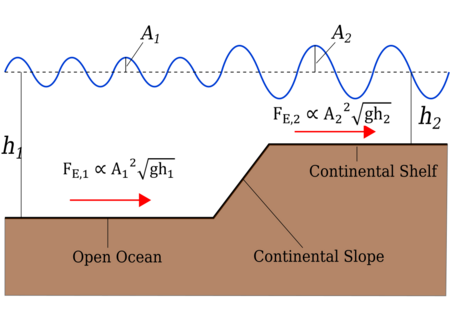
The transition from the deep ocean to the continental shelf, known as the continental slope, is characterized by a sudden decrease in water depth. In order to apply to the conservation of energy, the tidal wave has to deform as a result of the decrease in water depth. The total energy of a linear progressive wave per wavelength is the sum of the potential energy (PE) and the kinetic energy (KE). The potential and kinetic energy integrated over a complete wavelength are the same, under the assumption that the water level variations are small compared to the water depth ([math]\displaystyle{ \eta \lt \lt H }[/math]).[4]

[math]\displaystyle{ \int_{0}^{\lambda}PE = \int_{0}^{\lambda}KE = \frac{1}{2}\rho g\int_{0}^{\lambda}\eta^2 dx }[/math]

Figure 1: Tidal wave transmission on the continental shelf. At the transition from the open ocean to the continental shelf, the water depth decreases abruptly. As a result the tidal wave speed decreases as its phase and group speed are dependent on depth. In order to conserve the energy flux, the amplitude of the tidal wave has to increase on the continental shelf.

where [math]\displaystyle{ \rho }[/math] is the density, [math]\displaystyle{ g }[/math] the gravitation acceleration and [math]\displaystyle{ \eta }[/math] the vertical tidal elevation. The total wave energy becomes:

[math]\displaystyle{ E =\rho g\int_{0}^{\lambda}\eta^2 dx }[/math]

If we now solve for a harmonic wave [math]\displaystyle{ \eta(x) = Acos(kx) }[/math], where [math]\displaystyle{ k }[/math] is the wave number and [math]\displaystyle{ A }[/math] the amplitude, the total energy per unit area of surface becomes:[5]

[math]\displaystyle{ E_{s} = \frac{1}{2}\rho g A^2 }[/math]

A tidal wave has a wavelength that is much larger than the water depth. And thus according to the dispersion of gravity waves, they travel with the phase and group velocity of a shallow water wave: [math]\displaystyle{ c_p = c_g = \sqrt{gh} }[/math]. The wave energy is transmitted by the group velocity of a wave[6] and thus the energy flux ([math]\displaystyle{ F_E }[/math]) is given by:

[math]\displaystyle{ F_E = \frac{1}{2}\rho g A^2 \sqrt{gh} }[/math]

The energy flux needs to be conserved and with [math]\displaystyle{ \rho }[/math] and [math]\displaystyle{ g }[/math] constant, this leads to:

[math]\displaystyle{ F_{E,1}=F_{E,2}\Longrightarrow{A_1}^{2}\sqrt{gh_1} = {A_2}^{2}\sqrt{gh_2} }[/math]

where [math]\displaystyle{ h2\lt h1 }[/math] and thus [math]\displaystyle{ A_2 \gt A_1 }[/math].

When the tidal wave propagates onto the continental shelf, the water depth [math]\displaystyle{ (h) }[/math] decreases. In order to conserve the energy flux, the amplitude of the wave needs to increase (see figure 1).

Transmission coefficient

The above explanation is a simplification as not all tidal wave energy is transmitted, but it is partly reflected at the continental slope. The transmission coefficient of the tidal wave is given by:

[math]\displaystyle{ \frac{A_2}{A_1}=\frac{2 c_1}{(c_1+c_2)} }[/math][4]

This equation indicates that when [math]\displaystyle{ c_1 = c_2 }[/math] the transmitted tidal wave has the same amplitude as the original wave. Furthermore, the transmitted wave will be larger than the original wave when [math]\displaystyle{ c_1\gt c_2 }[/math] as is the case for the transition to the continental shelf.

The reflected wave amplitude ([math]\displaystyle{ A^' }[/math]) is determined by the reflection coefficient of the tidal wave:

[math]\displaystyle{ \frac{A^'}{A_1}=\frac{c_1-c_2}{(c_1+c_2)} }[/math][4]

This equation indicates that when [math]\displaystyle{ c_1 = c_2 }[/math] there is no reflected wave and if [math]\displaystyle{ c_1\gt c_2 }[/math] the reflected tidal wave will be smaller than the original tidal wave.

Internal tide and mixing

At the continental shelf the reflection and transmission of the tidal wave can lead to the generation of internal tides on the pycnocline. The surface (i.e. barotropic) tide generates these internal tides where stratified waters are forced upwards over a sloping bottom topography.[7] The internal tide extracts energy from the surface tide and propagates both in shoreward and seaward direction.[8] The shoreward propagating internal waves shoals when reaching shallower water where the wave energy is dissipated by wave breaking. The shoaling of the internal tide drives mixing across the pycnocline, high levels carbon sequestration and sediment resuspension.[9][10] Furthermore, through nutrient mixing the shoaling of the internal tide has a fundamental control on the functioning of ecosystems on the continental margin.[11]

Tidal propagation along coasts

After entering the continental shelf, a tidal wave quickly faces a boundary in the form of a landmass. When the tidal wave reaches a continental margin, it continues as a boundary trapped Kelvin wave. Along the coast, a boundary trapped Kelvin is also known as a coastal Kelvin wave or Edge wave. A Kelvin wave is a special type of gravity wave that can exist when there is (1) gravity and stable stratification, (2) sufficient Coriolis force and (3) the presence of a vertical boundary.[12] Kelvin waves are important in the ocean and shelf seas, they form a balance between inertia, the Coriolis force and the pressure gradient force. The simplest equations that describe the dynamics of Kelvin waves are the linearized shallow water equations for homogeneous, in-viscid flows. These equations can be linearized for a small Rossby number, no frictional forces and under the assumption that the wave height is small compared to the water depth ([math]\displaystyle{ \eta\lt \lt h }[/math]). The linearized depth-averaged shallow water equations become:

u momentum equation:

  • [math]\displaystyle{ \frac{\partial u}{\partial t} - fv = -g \frac{\partial\eta}{\partial x} }[/math]

v momentum equation:

  • [math]\displaystyle{ \frac{\partial v}{\partial t} + fu = -g \frac{\partial\eta}{\partial y} }[/math]

the continuity equation:

  • [math]\displaystyle{ \frac{\partial \eta}{\partial t} + h(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}) = 0 }[/math]

where [math]\displaystyle{ u }[/math] is the zonal velocity ([math]\displaystyle{ x }[/math] direction), [math]\displaystyle{ v }[/math] the meridional velocity ([math]\displaystyle{ y }[/math] direction), [math]\displaystyle{ t }[/math] is time and [math]\displaystyle{ f }[/math] is the Coriolis frequency.

Kelvin waves are named after Lord Kelvin, who first described them after finding solutions to the linearized shallow water equations with the boundary condition [math]\displaystyle{ u(x,y,t) = 0 }[/math].[13] When this assumption is made the linearized depth-averaged shallow water equations that can describe a Kelvin wave become:

u momentum equation:

  • [math]\displaystyle{ v = \frac{-g}{f} \frac{\partial\eta}{\partial x} }[/math]

v momentum equation:

  • [math]\displaystyle{ \frac{\partial v}{\partial t} = -g \frac{\partial\eta}{\partial y} }[/math]

the continuity equation:

  • [math]\displaystyle{ \frac{\partial \eta}{\partial t} + h\frac{\partial v}{\partial y} = 0 }[/math]

Now it is possible to get an expression for [math]\displaystyle{ \eta }[/math], by taking the time derivative of the continuity equation and substituting the momentum equation:

  • [math]\displaystyle{ \frac{\partial^2 \eta}{\partial t^2} - gh\frac{\partial^2 \eta}{\partial y^2} = 0 }[/math]

The same can be done for [math]\displaystyle{ v }[/math], by taking the time derivative of the v momentum equation and substituting the continuity equation

  • [math]\displaystyle{ \frac{\partial^2 v}{\partial t^2} - gh\frac{\partial^2 v}{\partial y^2} = 0 }[/math]

Both of these equations take the form of the classical wave equation, where [math]\displaystyle{ c = \sqrt{gh} }[/math]. Which is the same velocity as the tidal wave and thus of a shallow water wave. These preceding equations govern the dynamics of a one-dimensional non-dispersive wave, for which the following general solution exist:

  • [math]\displaystyle{ \eta = -h \ F(y + ct) \ e^{\frac{-x}{R}} }[/math]
  • [math]\displaystyle{ v = \sqrt{gh}\ F(y + ct) \ e^{\frac{-x}{R}} }[/math]

where length [math]\displaystyle{ R = \frac{\sqrt{gh}}{f} }[/math] is the Rossby radius of deformation and [math]\displaystyle{ F(y + ct) }[/math] is an arbitrary function describing the wave motion. In the most simple form [math]\displaystyle{ F }[/math] is a cosine or sine function which describes a wave motion in the positive and negative direction. The Rossby radius of deformation is a typical length scale in the ocean and atmosphere that indicates when rotational effects become important. The Rossby radius of deformation is a measure for the trapping distance of a coastal Kelvin wave.[14] The exponential term results in an amplitude that decays away from the coast.

The expression of tides as a bounded Kelvin wave is well observable in enclosed shelf seas around the world (e.g. the English channel, the North Sea or the Yellow sea). Animation 1 shows the behaviour of a simplified case of a Kelvin wave in an enclosed shelf sea for the case with (lower panel) and without friction (upper panel). The shape of an enclosed shelf sea is represented as a simple rectangular domain in the Northern Hemisphere which is open on the left hand side and closed on the right hand side. The tidal wave, a Kelvin wave, enters the domain in the lower left corner and travels to the right with the coast on its right. The sea surface height (SSH, left panels of animation 1), the tidal elevation, is maximum at the coast and decreases towards the centre of the domain. The tidal currents (right panels of animation 1) are in the direction of wave propagation under the crest and in the opposite direction under the through. They are both maximum under the crest and the trough of the waves and decrease towards the centre. This was expected as the equations for [math]\displaystyle{ \eta }[/math] and [math]\displaystyle{ v }[/math] are in phase as they both depend on the same arbitrary function describing the wave motion and exponential decay term. Therefore this set of equations describes a wave that travels along the coast with a maximum amplitude at the coast which declines towards the ocean. These solutions also indicate that a Kelvin wave always travels with the coast on their right hand side in the Northern Hemisphere and with the coast at their left hand side in the Southern Hemisphere. In the limit of no rotation where [math]\displaystyle{ f \rightarrow 0 }[/math], the exponential term increase without a bound and the wave will become a simple gravity wave orientated perpendicular to the coast.[14] In the next section, it will be shown how these Kelvin waves behaves when traveling along a coast, in an enclosed shelf seas or in estuaries and basins.

Tides in enclosed shelf seas

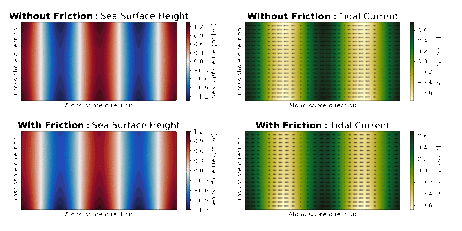
Animation 1: A traveling Kelvin wave is shown for the Northern hemisphere with (lower panel) and without (upper panel) friction, the coast is always at the right of the direction of motion. The domain is closed on the right hand side, to mimic an enclosed shelf sea. The wave enters the domain on the lower left hand side and travels towards the right. On the right hand side the wave is reflected and travels back towards the left. On the closed side the reflection happens through the creation of Poincare waves which are not modelled here. The panels on the left shows the sea surface height and the panels on the right the velocity. The colours are indicated in the colour bar, the arrows are scaled velocity vectors

thumb|462x462px|Figure 2: The time averaged sea surface height is shown in red shading and the dashed lines are cotidal lines at intervals of roughly an hour. The Amphidromic points are located at the intersect of all lines. The upper panel shows the case for without friction and the lower panel for the case with frictionThe expression of tides as a bounded Kelvin wave is well observable in enclosed shelf seas around the world (e.g. the English channel, the North Sea or the Yellow sea). Animation 1 shows the behaviour of a simplified case of a Kelvin wave in an enclosed shelf sea for the case with (lower panel) and without friction (upper panel). The shape of an enclosed shelf sea is represented as a simple rectangular domain in the Northern Hemisphere which is open on the left hand side and closed on the right hand side. The tidal wave, a Kelvin wave, enters the domain in the lower left corner and travels to the right with the coast on its right. The sea surface height (SSH, left panels of animation 1), the tidal elevation, is maximum at the coast and decreases towards the centre of the domain. The tidal currents (right panels of animation 1) are in the direction of wave propagation under the crest and in the opposite direction under the through. They are both maximum under the crest and the trough of the waves and decrease towards the centre. This was expected as the equations for [math]\displaystyle{ \eta }[/math] and [math]\displaystyle{ v }[/math] are in phase as they both depend on the same arbitrary function describing the wave motion and exponential decay term.

On the enclosed right hand side, the Kelvin wave is reflected and because it always travels with the coast on its right, it will now travel in the opposite direction. The energy of the incoming Kelvin wave is transferred through Poincare waves along the enclosed side of the domain to the outgoing Kelvin wave. The final pattern of the SSH and the tidal currents is made up of the sum of the two Kelvin waves. These two can amplify each other and this amplification is maximum when the length of the shelf sea is a quarter wavelength of the tidal wave.[2] Next to that, the sum of the two Kelvin waves result in several static minima's in the centre of the domain which hardly experience any tidal motion, these are called Amphidromic points. In the upper panel of figure 2, the absolute time averaged SSH is shown in red shading and the dotted lines show the zero tidal elevation level at roughly hourly intervals, also known as cotidal lines. Where these lines intersect the tidal elevation is zero during a full tidal period and thus this is the location of the Amphidromic points.

In the real world, the reflected Kelvin wave has a lower amplitude due to energy loss as a result of friction and through the transfer via Poincare waves (lower left panel of animation 1). The tidal currents are proportional to the wave amplitude and therefore also decrease on the side of the reflected wave (lower right panel of animation 1). Finally, the static minima's are no longer in the centre of the domain as wave amplitude is no longer symmetric. Therefore, the Amphidromic points shift towards the side of the reflected wave (lower panel figure 2).

The dynamics of a tidal Kelvin wave in enclosed shelf sea is well manifested and studied in the North Sea.[15]

Tides in estuaries and basins

When tides enter estuaries or basins, the boundary conditions change as the geometry changes drastically. The water depth becomes shallower and the width decreases, next to that the depth and width become significantly variable over the length and width of the estuary or basin. As a result the tidal wave deforms which affects the tidal amplitude, phase speed and the relative phase between tidal velocity and elevation. The deformation of the tide is largely controlled by the competition between bottom friction and channel convergence.[16] Channel convergence increases the tidal amplitude and phase speed as the energy of the tidal wave is traveling through a smaller area while bottom friction decrease the amplitude through energy loss.[17] The modification of the tide leads to the creation of overtides (e.g. [math]\displaystyle{ M_{4} }[/math] tidal constituents) or higher harmonics. These overtides are multiples, sums or differences of the astronomical tidal constituents and as a result the tidal wave can become asymmetric.[18] A tidal asymmetry is a difference between the duration of the rise and the fall of the tidal water elevation and this can manifest itself as a difference in flood/ebb tidal currents.[19] The tidal asymmetry and the resulting currents are important for the sediment transport and turbidity in estuaries and tidal basins.[20] Each estuary and basin has its own distinct geometry and these can be subdivided in several groups of similar geometries with its own tidal dynamics.[16]

See also

References

  1. ↑ https://beltoforion.de/en/tides/simulation.php Tidal forces explained
  2. ↑ 2.0 2.1 Pugh, David; Woodworth, Philip (2014). Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes. Cambridge: Cambridge University Press. pp. 97–132. doi:10.1017/cbo9781139235778. ISBN 978-1-107-02819-7. https://www.cambridge.org/core/books/sealevel-science/C5E551D95DA4E8AF116FED9F0DEB289B. 
  3. ↑ Parker, Bruce B.; Davies, Alan M.; Xing, Jiuxing (1999), "Tidal height and current prediction", Coastal and Estuarine Studies (Washington, D. C.: American Geophysical Union): pp. 277–327, doi:10.1029/ce056p0277, ISBN 0-87590-270-7, http://dx.doi.org/10.1029/ce056p0277, retrieved 2021-05-13 
  4. ↑ 4.0 4.1 4.2 Pugh, David; Woodworth, Philip (2014). Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes. Cambridge: Cambridge University Press. pp. 370–375. doi:10.1017/cbo9781139235778. ISBN 978-1-107-02819-7. https://www.cambridge.org/core/books/sealevel-science/C5E551D95DA4E8AF116FED9F0DEB289B. 
  5. ↑ "Wave Energy - Energy associated with wave motion.". http://web.mit.edu/fluids-modules/www/potential_flows/LecturesHTML/lec20/node3.html. 
  6. ↑ Cushman-Roisin, Benoit; Beckers, Jean-Marie (2011). Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects. Academic Press. pp. 778–780. doi:10.1016/c2009-0-00052-x. ISBN 978-0-12-088759-0. 
  7. ↑ Garrett, Chris; Kunze, Eric (2007-01-21). "Internal Tide Generation in the Deep Ocean" (in en). Annual Review of Fluid Mechanics 39 (1): 57–87. doi:10.1146/annurev.fluid.39.050905.110227. ISSN 0066-4189. Bibcode: 2007AnRFM..39...57G. http://www.annualreviews.org/doi/10.1146/annurev.fluid.39.050905.110227. 
  8. ↑ Holloway, Peter E.; Chatwin, Paul G.; Craig, Peter (2001-06-06). "Internal Tide Observations from the Australian North West Shelf in Summer 1995". Journal of Physical Oceanography 31 (5): 1182–1199. doi:10.1175/1520-0485(2001)031<1182:itofta>2.0.co;2. ISSN 0022-3670. Bibcode: 2001JPO....31.1182H. 
  9. ↑ Palmer, M.R.; Stephenson, G.R.; Inall, M.E.; Balfour, C.; Düsterhus, A.; Green, J.A.M. (2015-04-01). "Turbulence and mixing by internal waves in the Celtic Sea determined from ocean glider microstructure measurements". Journal of Marine Systems 144: 57–69. doi:10.1016/j.jmarsys.2014.11.005. ISSN 0924-7963. Bibcode: 2015JMS...144...57P. 
  10. ↑ Kelly, S. M.; Nash, J. D. (2010-12-10). "Internal-tide generation and destruction by shoaling internal tides". Geophysical Research Letters 37 (23): n/a. doi:10.1029/2010gl045598. ISSN 0094-8276. Bibcode: 2010GeoRL..3723611K. 
  11. ↑ Sharples, Jonathan; Moore, C. Mark; Hickman, Anna E.; Holligan, Patrick M.; Tweddle, Jacqueline F.; Palmer, Matthew R.; Simpson, John H. (2009-12-02). "Internal tidal mixing as a control on continental margin ecosystems". Geophysical Research Letters 36 (23). doi:10.1029/2009gl040683. ISSN 0094-8276. Bibcode: 2009GeoRL..3623603S. http://dx.doi.org/10.1029/2009gl040683. 
  12. ↑ Wang, B. (2003), Kelvin Waves, Elsevier, pp. 1062–1068, doi:10.1016/b0-12-227090-8/00191-3, ISBN 978-0-12-227090-1, http://dx.doi.org/10.1016/b0-12-227090-8/00191-3, retrieved 2021-05-17 
  13. ↑ "Midlatitude Dynamics and Quasi-Geostrophic Models" (in en). International Geophysics 66: 291–336. 2000-01-01. doi:10.1016/S0074-6142(00)80009-1. ISBN 9780124340688. ISSN 0074-6142. https://www.sciencedirect.com/science/article/pii/S0074614200800091. 
  14. ↑ 14.0 14.1 Cushman-Roisin, Benoit; Beckers, Jean-Marie (2011). Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects. Academic Press. pp. 273–276. doi:10.1016/c2009-0-00052-x. ISBN 978-0-12-088759-0. 
  15. ↑ Roos, Pieter C.; Velema, Jorick J.; Hulscher, Suzanne J. M. H.; Stolk, Ad (2011-07-19). "An idealized model of tidal dynamics in the North Sea: resonance properties and response to large-scale changes". Ocean Dynamics 61 (12): 2019–2035. doi:10.1007/s10236-011-0456-x. ISSN 1616-7341. Bibcode: 2011OcDyn..61.2019R. 
  16. ↑ 16.0 16.1 Friedrichs, Carl T. (2010), Valle-Levinson, Arnoldo, ed., "Barotropic tides in channelized estuaries", Contemporary Issues in Estuarine Physics (Cambridge: Cambridge University Press): pp. 27–61, doi:10.1017/cbo9780511676567.004, ISBN 978-0-511-67656-7, https://www.cambridge.org/core/product/identifier/CBO9780511676567A009/type/book_part, retrieved 2021-05-18 
  17. ↑ Friedrichs, Carl T.; Aubrey, David G. (1994). "Tidal propagation in strongly convergent channels". Journal of Geophysical Research 99 (C2): 3321. doi:10.1029/93jc03219. ISSN 0148-0227. Bibcode: 1994JGR....99.3321F. http://dx.doi.org/10.1029/93jc03219. 
  18. ↑ Pugh, David; Woodworth, Philip (2014). Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes. Cambridge: Cambridge University Press. pp. 133–154. doi:10.1017/cbo9781139235778. ISBN 978-1-107-02819-7. https://www.cambridge.org/core/books/sealevel-science/C5E551D95DA4E8AF116FED9F0DEB289B. 
  19. ↑ Cavalcante, Geórgenes H. (2016), Kennish, Michael J., ed., Tidal Asymmetry, Encyclopedia of Earth Sciences Series, Dordrecht: Springer Netherlands, pp. 664, doi:10.1007/978-94-017-8801-4_183, ISBN 978-94-017-8800-7, http://link.springer.com/10.1007/978-94-017-8801-4_183, retrieved 2021-05-18 
  20. ↑ Gallo, Marcos Nicolás; Vinzon, Susana Beatriz (2005-08-30). "Generation of overtides and compound tides in Amazon estuary". Ocean Dynamics 55 (5–6): 441–448. doi:10.1007/s10236-005-0003-8. ISSN 1616-7341. Bibcode: 2005OcDyn..55..441G. http://dx.doi.org/10.1007/s10236-005-0003-8. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Astronomy:Tides_in_marginal_seas&oldid=3346506"