Physics:Conservation of energy
| Continuum mechanics |
|---|
In physics and chemistry, the law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be conserved over time.[1] In the case of a closed system the principle says that the total amount of energy within the system can only be changed through energy entering or leaving the system. Energy can neither be created nor destroyed; rather, it can only be transformed or transferred from one form to another. For instance, chemical energy is converted to kinetic energy when a stick of dynamite explodes. If one adds up all forms of energy that were released in the explosion, such as the kinetic energy and potential energy of the pieces, as well as heat and sound, one will get the exact decrease of chemical energy in the combustion of the dynamite.
Classically, conservation of energy was distinct from conservation of mass. However, special relativity shows that mass is related to energy and vice versa by , the equation representing mass–energy equivalence, and science now takes the view that mass-energy as a whole is conserved. Theoretically, this implies that any object with mass can itself be converted to pure energy, and vice versa. However, this is believed to be possible only under the most extreme of physical conditions, such as likely existed in the universe very shortly after the Big Bang or when black holes emit Hawking radiation.
Given the stationary-action principle, conservation of energy can be rigorously proven by Noether's theorem as a consequence of continuous time translation symmetry; that is, from the fact that the laws of physics do not change over time.
A consequence of the law of conservation of energy is that a perpetual motion machine of the first kind cannot exist; that is to say, no system without an external energy supply can deliver an unlimited amount of energy to its surroundings.[2] Depending on the definition of energy, conservation of energy can arguably be violated by general relativity on the cosmological scale.[3]
History
Ancient philosophers as far back as Thales of Miletus c. 550 BCE had inklings of the conservation of some underlying substance of which everything is made. However, there is no particular reason to identify their theories with what we know today as "mass-energy" (for example, Thales thought it was water). Empedocles (490–430 BCE) wrote that in his universal system, composed of four roots (earth, air, water, fire), "nothing comes to be or perishes";[4] instead, these elements suffer continual rearrangement. Epicurus (c. 350 BCE) on the other hand believed everything in the universe to be composed of indivisible units of matter—the ancient precursor to 'atoms'—and he too had some idea of the necessity of conservation, stating that "the sum total of things was always such as it is now, and such it will ever remain."[5]
In 1605, the Flemish scientist Simon Stevin was able to solve a number of problems in statics based on the principle that perpetual motion was impossible.
In 1639, Galileo published his analysis of several situations—including the celebrated "interrupted pendulum"—which can be described (in modern language) as conservatively converting potential energy to kinetic energy and back again. Essentially, he pointed out that the height a moving body rises is equal to the height from which it falls, and used this observation to infer the idea of inertia. The remarkable aspect of this observation is that the height to which a moving body ascends on a frictionless surface does not depend on the shape of the surface.
In 1669, Christiaan Huygens published his laws of collision. Among the quantities he listed as being invariant before and after the collision of bodies were both the sum of their linear momenta as well as the sum of their kinetic energies. However, the difference between elastic and inelastic collision was not understood at the time. This led to the dispute among later researchers as to which of these conserved quantities was the more fundamental. In his Horologium Oscillatorium, he gave a much clearer statement regarding the height of ascent of a moving body, and connected this idea with the impossibility of perpetual motion. Huygens's study of the dynamics of pendulum motion was based on a single principle: that the center of gravity of a heavy object cannot lift itself.

Between 1676 and 1689, Gottfried Leibniz first attempted a mathematical formulation of the kind of energy that is associated with motion (kinetic energy). Using Huygens's work on collision, Leibniz noticed that in many mechanical systems (of several masses mi, each with velocity vi),
was conserved so long as the masses did not interact. He called this quantity the vis viva or living force of the system. The principle represents an accurate statement of the approximate conservation of kinetic energy in situations where there is no friction. Many physicists at that time, including Isaac Newton, held that the conservation of momentum, which holds even in systems with friction, as defined by the momentum:
was the conserved vis viva. It was later shown that both quantities are conserved simultaneously given the proper conditions, such as in an elastic collision.
In 1687, Isaac Newton published his Principia, which set out his laws of motion. It was organized around the concept of force and momentum. However, the researchers were quick to recognize that the principles set out in the book, while fine for point masses, were not sufficient to tackle the motions of rigid and fluid bodies. Some other principles were also required.
By the 1690s, Leibniz was arguing that conservation of vis viva and conservation of momentum undermined the then-popular philosophical doctrine of interactionist dualism. (During the 19th century, when conservation of energy was better understood, Leibniz's basic argument would gain widespread acceptance. Some modern scholars continue to champion specifically conservation-based attacks on dualism, while others subsume the argument into a more general argument about causal closure.)[6]

The law of conservation of vis viva was championed by the father and son duo, Johann and Daniel Bernoulli. The former enunciated the principle of virtual work as used in statics in its full generality in 1715, while the latter based his Hydrodynamica, published in 1738, on this single vis viva conservation principle. Daniel's study of loss of vis viva of flowing water led him to formulate the Bernoulli's principle, which asserts the loss to be proportional to the change in hydrodynamic pressure. Daniel also formulated the notion of work and efficiency for hydraulic machines; and he gave a kinetic theory of gases, and linked the kinetic energy of gas molecules with the temperature of the gas.
This focus on the vis viva by the continental physicists eventually led to the discovery of stationarity principles governing mechanics, such as the D'Alembert's principle, Lagrangian, and Hamiltonian formulations of mechanics.

Émilie du Châtelet (1706–1749) proposed and tested the hypothesis of the conservation of total energy, as distinct from momentum. Inspired by the theories of Gottfried Leibniz, she repeated and publicized an experiment originally devised by Willem 's Gravesande in 1722 in which balls were dropped from different heights into a sheet of soft clay. Each ball's kinetic energy—as indicated by the quantity of material displaced—was shown to be proportional to the square of the velocity. The deformation of the clay was found to be directly proportional to the height from which the balls were dropped, equal to the initial potential energy. Some earlier workers, including Newton and Voltaire, had believed that "energy" was not distinct from momentum and therefore proportional to velocity. According to this understanding, the deformation of the clay should have been proportional to the square root of the height from which the balls were dropped. In classical physics, the correct formula is , where is the kinetic energy of an object, its mass and its speed. On this basis, du Châtelet proposed that energy must always have the same dimensions in any form, which is necessary to be able to consider it in different forms (kinetic, potential, heat, ...).[7][8]
Engineers such as John Smeaton, Peter Ewart, Carl Holtzmann, Gustave-Adolphe Hirn, and Marc Seguin recognized that conservation of momentum alone was not adequate for practical calculation and made use of Leibniz's principle. The principle was also championed by some chemists such as William Hyde Wollaston. Academics such as John Playfair were quick to point out that kinetic energy is clearly not conserved. This is obvious to a modern analysis based on the second law of thermodynamics, but in the 18th and 19th centuries, the fate of the lost energy was still unknown.
Gradually it came to be suspected that the heat inevitably generated by motion under friction was another form of vis viva. In 1783, Antoine Lavoisier and Pierre-Simon Laplace reviewed the two competing theories of vis viva and caloric theory.[9][10] Count Rumford's 1798 observations of heat generation during the boring of cannons added more weight to the view that mechanical motion could be converted into heat and (that it was important) that the conversion was quantitative and could be predicted (allowing for a universal conversion constant between kinetic energy and heat). Vis viva then started to be known as energy, after the term was first used in that sense by Thomas Young in 1807.

The recalibration of vis viva to
which can be understood as converting kinetic energy to work, was largely the result of Gaspard-Gustave Coriolis and Jean-Victor Poncelet over the period 1819–1839. The former called the quantity quantité de travail (quantity of work) and the latter, travail mécanique (mechanical work), and both championed its use in engineering calculations.
In the paper Über die Natur der Wärme (German "On the Nature of Heat/Warmth"), published in the Zeitschrift für Physik in 1837, Karl Friedrich Mohr gave one of the earliest general statements of the doctrine of the conservation of energy: "besides the 54 known chemical elements there is in the physical world one agent only, and this is called Kraft [energy or work]. It may appear, according to circumstances, as motion, chemical affinity, cohesion, electricity, light and magnetism; and from any one of these forms it can be transformed into any of the others."
Mechanical equivalent of heat
A key stage in the development of the modern conservation principle was the demonstration of the mechanical equivalent of heat. The caloric theory maintained that heat could neither be created nor destroyed, whereas conservation of energy entails the contrary principle that heat and mechanical work are interchangeable.
In the middle of the eighteenth century, Mikhail Lomonosov, a Russian scientist, postulated his corpusculo-kinetic theory of heat, which rejected the idea of a caloric. Through the results of empirical studies, Lomonosov came to the conclusion that heat was not transferred through the particles of the caloric fluid.
In 1798, Count Rumford (Benjamin Thompson) performed measurements of the frictional heat generated in boring cannons and developed the idea that heat is a form of kinetic energy; his measurements refuted caloric theory, but were imprecise enough to leave room for doubt.
The mechanical equivalence principle was first stated in its modern form by the German surgeon Julius Robert von Mayer in 1842.[11] Mayer reached his conclusion on a voyage to the Dutch East Indies, where he found that his patients' blood was a deeper red because they were consuming less oxygen, and therefore less energy, to maintain their body temperature in the hotter climate. He discovered that heat and mechanical work were both forms of energy, and in 1845, after improving his knowledge of physics, he published a monograph that stated a quantitative relationship between them.[12]
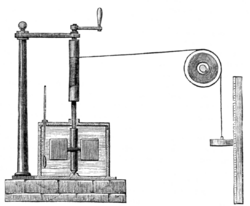
Meanwhile, in 1843, James Prescott Joule independently discovered the mechanical equivalent in a series of experiments. In the most famous, now called the "Joule apparatus", a descending weight attached to a string caused a paddle immersed in water to rotate. He showed that the gravitational potential energy lost by the weight in descending was equal to the internal energy gained by the water through friction with the paddle.
Over the period 1840–1843, similar work was carried out by engineer Ludwig A. Colding, although it was little known outside his native Denmark.
Both Joule's and Mayer's work suffered from resistance and neglect but it was Joule's that eventually drew the wider recognition.
In 1844, the Welsh scientist William Robert Grove postulated a relationship between mechanics, heat, light, electricity, and magnetism by treating them all as manifestations of a single "force" (energy in modern terms). In 1846, Grove published his theories in his book The Correlation of Physical Forces.[13] In 1847, drawing on the earlier work of Joule, Sadi Carnot, and Émile Clapeyron, Hermann von Helmholtz arrived at conclusions similar to Grove's and published his theories in his book Über die Erhaltung der Kraft (On the Conservation of Force, 1847).[14] The general modern acceptance of the principle stems from this publication.
In 1850, the Scottish mathematician William Rankine first used the phrase the law of the conservation of energy for the principle.[15]
In 1877, Peter Guthrie Tait claimed that the principle originated with Sir Isaac Newton, based on a creative reading of propositions 40 and 41 of the Philosophiae Naturalis Principia Mathematica. This is now regarded as an example of Whig history.[16]
Mass–energy equivalence
Matter is composed of atoms and what makes up atoms. Matter has intrinsic or rest mass. In the limited range of recognized experience of the nineteenth century, it was found that such rest mass is conserved. Einstein's 1905 theory of special relativity showed that rest mass corresponds to an equivalent amount of rest energy. This means that rest mass can be converted to or from equivalent amounts of (non-material) forms of energy, for example, kinetic energy, potential energy, and electromagnetic radiant energy. When this happens, as recognized in twentieth-century experience, rest mass is not conserved, unlike the total mass or total energy. All forms of energy contribute to the total mass and total energy.
For example, an electron and a positron each have rest mass. They can perish together, converting their combined rest energy into photons which have electromagnetic radiant energy but no rest mass. If this occurs within an isolated system that does not release the photons or their energy into the external surroundings, then neither the total mass nor the total energy of the system will change. The produced electromagnetic radiant energy contributes just as much to the inertia (and to any weight) of the system as did the rest mass of the electron and positron before their demise. Likewise, non-material forms of energy can perish into matter, which has rest mass.
Thus, conservation of energy (total, including material or rest energy) and conservation of mass (total, not just rest) are one (equivalent) law. In the 18th century, these had appeared as two seemingly-distinct laws.
Conservation of energy in beta decay
The discovery in 1911 that electrons emitted in beta decay have a continuous rather than a discrete spectrum appeared to contradict conservation of energy, under the then-current assumption that beta decay is the simple emission of an electron from a nucleus.[17][18] This problem was eventually resolved in 1933 by Enrico Fermi who proposed the correct description of beta-decay as the emission of both an electron and an antineutrino, which carries away the apparently missing energy.[19][20]
First law of thermodynamics
For a closed thermodynamic system, the first law of thermodynamics may be stated as:
- , or equivalently,
where is the quantity of energy added to the system by a heating process, is the quantity of energy lost by the system due to work done by the system on its surroundings, and is the change in the internal energy of the system.
The δ's before the heat and work terms are used to indicate that they describe an increment of energy which is to be interpreted somewhat differently than the increment of internal energy (see Inexact differential). Work and heat refer to kinds of process which add or subtract energy to or from a system, while the internal energy is a property of a particular state of the system when it is in unchanging thermodynamic equilibrium. Thus the term "heat energy" for means "that amount of energy added as a result of heating" rather than referring to a particular form of energy. Likewise, the term "work energy" for means "that amount of energy lost as a result of work". Thus one can state the amount of internal energy possessed by a thermodynamic system that one knows is presently in a given state, but one cannot tell, just from knowledge of the given present state, how much energy has in the past flowed into or out of the system as a result of its being heated or cooled, nor as a result of work being performed on or by the system.
Entropy is a function of the state of a system which tells of limitations of the possibility of conversion of heat into work.
For a simple compressible system, the work performed by the system may be written:
where is the pressure and is a small change in the volume of the system, each of which are system variables. In the fictive case in which the process is idealized and infinitely slow, so as to be called quasi-static, and regarded as reversible, the heat being transferred from a source with temperature infinitesimally above the system temperature, the heat energy may be written
where is the temperature and is a small change in the entropy of the system. Temperature and entropy are variables of the state of a system.
If an open system (in which mass may be exchanged with the environment) has several walls such that the mass transfer is through rigid walls separate from the heat and work transfers, then the first law may be written as[21]
where is the added mass of species and is the corresponding enthalpy per unit mass. Note that generally in this case, as matter carries its own entropy. Instead, , where is the entropy per unit mass of type , from which we recover the fundamental thermodynamic relation
because the chemical potential is the partial molar Gibbs free energy of species and the Gibbs free energy .
Noether's theorem

The conservation of energy is a common feature in many physical theories. From a mathematical point of view it is understood as a consequence of Noether's theorem, developed by Emmy Noether in 1915 and first published in 1918. In any physical theory that obeys the stationary-action principle, the theorem states that every continuous symmetry has an associated conserved quantity; if the theory's symmetry is time invariance, then the conserved quantity is called "energy".[22] The energy conservation law is a consequence of the shift symmetry of time; energy conservation is implied by the empirical fact that the laws of physics do not change with time itself. Philosophically this can be stated as "nothing depends on time per se". In other words, if the physical system is invariant under the continuous symmetry of time translation, then its energy (which is the canonical conjugate quantity to time) is conserved. Conversely, systems that are not invariant under shifts in time (e.g. systems with time-dependent potential energy) do not exhibit conservation of energy – unless we consider them to exchange energy with another, an external system so that the theory of the enlarged system becomes time-invariant again. Conservation of energy for finite systems is valid in physical theories such as special relativity and quantum theory (including QED) in the flat space-time.
Special relativity
With the discovery of special relativity by Henri Poincaré and Albert Einstein, the energy was proposed to be a component of an energy-momentum 4-vector. Each of the four components (one of energy and three of momentum) of this vector is separately conserved across time, in any closed system, as seen from any given inertial reference frame. Also conserved is the vector length (Minkowski norm), which is the rest mass for single particles, and the invariant mass for systems of particles (where momenta and energy are separately summed before the length is calculated).
The relativistic energy of a single massive particle contains a term related to its rest mass in addition to its kinetic energy of motion. In the limit of zero kinetic energy (or equivalently in the rest frame) of a massive particle, or else in the center of momentum frame for objects or systems which retain kinetic energy, the total energy of a particle or object (including internal kinetic energy in systems) is proportional to the rest mass or invariant mass, as described by the famous equation .
Thus, the rule of conservation of energy over time in special relativity continues to hold, so long as the reference frame of the observer is unchanged. This applies to the total energy of systems, although different observers disagree as to the energy value. Also conserved, and invariant to all observers, is the invariant mass, which is the minimal system mass and energy that can be seen by any observer, and which is defined by the energy–momentum relation.
General relativity
General relativity introduces new phenomena. In an expanding universe, photons spontaneously redshift and tethers spontaneously gain tension; if vacuum energy is positive, the total vacuum energy of the universe appears to spontaneously increase as the volume of space increases. Some scholars claim that energy is no longer meaningfully conserved in any identifiable form.[23][24]
John Baez's view is that energy–momentum conservation is not well-defined except in certain special cases. Energy-momentum is typically expressed with the aid of a stress–energy–momentum pseudotensor. However, since pseudotensors are not tensors, they do not transform cleanly between reference frames. If the metric under consideration is static (that is, does not change with time) or asymptotically flat (that is, at an infinite distance away spacetime looks empty), then energy conservation holds without major pitfalls. In practice, some metrics, notably the Friedmann–Lemaître–Robertson–Walker metric that appears to govern the universe, do not satisfy these constraints and energy conservation is not well defined.[25] Besides being dependent on the coordinate system, pseudotensor energy is dependent on the type of pseudotensor in use; for example, the energy exterior to a Kerr–Newman black hole is twice as large when calculated from Møller's pseudotensor as it is when calculated using the Einstein pseudotensor.[26]
For asymptotically flat universes, Einstein and others salvage conservation of energy by introducing a specific global gravitational potential energy that cancels out mass-energy changes triggered by spacetime expansion or contraction. This global energy has no well-defined density and cannot technically be applied to a non-asymptotically flat universe; however, for practical purposes this can be finessed, and so by this view, energy is conserved in our universe.[27][3] Alan Guth even famously stated that the universe might be "the ultimate free lunch", and theorized that, when accounting for gravitational potential energy, the net energy of the Universe is zero.[28]
Quantum theory
In quantum mechanics, the energy of a quantum system is described by a self-adjoint (or Hermitian) operator called the Hamiltonian, which acts on the Hilbert space (or a space of wave functions) of the system. If the Hamiltonian is a time-independent operator, emergence probability of the measurement result does not change in time over the evolution of the system. Thus the expectation value of energy is also time independent. The local energy conservation in quantum field theory is ensured by the quantum Noether's theorem for the energy-momentum tensor operator. Thus energy is conserved by the normal unitary evolution of a quantum system.
However, when the non-unitary Born rule is applied, the system's energy is measured with an energy that can be below or above the expectation value, if the system was not in an energy eigenstate. (For macroscopic systems, this effect is usually too small to measure.) The disposition of this energy gap is not well-understood; some physicists believe that the energy is transferred to or from the macroscopic environment in the course of the measurement process, while others believe that the observable energy is only conserved "on average".[29][30] No experiment has been confirmed as definitive evidence of violations of the conservation of energy principle in quantum mechanics, but that doesn't rule out that some newer experiments, as proposed, may find evidence of violations of the conservation of energy principle in quantum mechanics.[30]
Status
In the context of perpetual motion machines such as the Orbo, Professor Eric Ash has argued at the BBC: "Denying [conservation of energy] would undermine not just little bits of science - the whole edifice would be no more. All of the technology on which we built the modern world would lie in ruins." It is because of conservation of energy that "we know - without having to examine details of a particular device - that Orbo cannot work."[31]
Energy conservation has been a foundational physical principle for about two hundred years. From the point of view of modern general relativity, the lab environment can be well approximated by Minkowski spacetime, where energy is exactly conserved. The entire Earth can be well approximated by the Schwarzschild metric, where again energy is exactly conserved. Given all the experimental evidence, any new theory (such as quantum gravity), in order to be successful, will have to explain why energy has appeared to always be exactly conserved in terrestrial experiments.[32] In some speculative theories, corrections to quantum mechanics are too small to be detected at anywhere near the current TeV level accessible through particle accelerators. Doubly special relativity models may argue for a breakdown in energy-momentum conservation for sufficiently energetic particles; such models are constrained by observations that cosmic rays appear to travel for billions of years without displaying anomalous non-conservation behavior.[33] Some interpretations of quantum mechanics claim that observed energy tends to increase when the Born rule is applied due to localization of the wave function. If true, objects could be expected to spontaneously heat up; thus, such models are constrained by observations of large, cool astronomical objects as well as the observation of (often supercooled) laboratory experiments.[34]
See also
- Energy quality
- Energy transformation
- Lagrangian mechanics
- Laws of thermodynamics
- Zero-energy universe
References
- ↑ Richard Feynman (1970). The Feynman Lectures on Physics Vol I. Addison Wesley. ISBN 978-0-201-02115-8. https://feynmanlectures.caltech.edu/I_04.html.
- ↑ Planck, M. (1923/1927). Treatise on Thermodynamics, third English edition translated by A. Ogg from the seventh German edition, Longmans, Green & Co., London, page 40.
- ↑ 3.0 3.1 "Energy Is Not Conserved" (in en). Discover Magazine. 2010. https://www.discovermagazine.com/the-sciences/energy-is-not-conserved.
- ↑ Janko, Richard (2004). "Empedocles, "On Nature"". Zeitschrift für Papyrologie und Epigraphik 150: 1–26. http://ancphil.lsa.umich.edu/-/downloads/faculty/janko/empedocles-nature.pdf.
- ↑ Laertius, Diogenes. Lives of Eminent Philosophers: Epicurus. https://www-loebclassics.com/view/diogenes_laertius-lives_eminent_philosophers_book_x_epicurus/1925/pb_LCL185.569.xml?result=1&rskey=YoU4V6.[yes|permanent dead link|dead link}}]. This passage comes from a letter quoted in full by Diogenes, and purportedly written by Epicurus himself in which he lays out the tenets of his philosophy.
- ↑ Pitts, J. Brian (September 2021). "Conservation of Energy: Missing Features in Its Nature and Justification and Why They Matter". Foundations of Science 26 (3): 559–584. doi:10.1007/s10699-020-09657-1. PMID 34759713.
- ↑ Hagengruber, Ruth, editor (2011) Émilie du Chatelet between Leibniz and Newton. Springer. ISBN:978-94-007-2074-9.
- ↑ Arianrhod, Robyn (2012). Seduced by logic : Émilie du Châtelet, Mary Somerville, and the Newtonian revolution (US ed.). New York: Oxford University Press. ISBN 978-0-19-993161-3. http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=9444991.
- ↑ Lavoisier, A.L. & Laplace, P.S. (1780) "Memoir on Heat", Académie Royale des Sciences pp. 4–355
- ↑ Guerlac, Henry (1976). "Chemistry as a Branch of Physics: Laplace's Collaboration with Lavoisier". Historical Studies in the Physical Sciences (University of California Press) 7: 193–276. doi:10.2307/27757357. https://online.ucpress.edu/hsns/article-abstract/doi/10.2307/27757357/47949/Chemistry-as-a-Branch-of-Physics-Laplace-s?redirectedFrom=fulltext. Retrieved 24 March 2022.
- ↑ von Mayer, J.R. (1842) "Remarks on the forces of inorganic nature" in Annalen der Chemie und Pharmacie, 43, 233
- ↑ Mayer, J.R. (1845). Die organische Bewegung in ihrem Zusammenhange mit dem Stoffwechsel. Ein Beitrag zur Naturkunde, Dechsler, Heilbronn.
- ↑ Grove, W. R. (1874). The Correlation of Physical Forces (6th ed.). London: Longmans, Green. https://archive.org/details/correlationphys06grovgoog.
- ↑ "On the Conservation of Force". Bartleby. http://www.bartleby.com/30/125.html.
- ↑ William John Macquorn Rankine (1853) "On the General Law of the Transformation of Energy," Proceedings of the Philosophical Society of Glasgow, vol. 3, no. 5, pages 276-280; reprinted in: (1) Philosophical Magazine, series 4, vol. 5, no. 30, pages 106-117 (February 1853); and (2) W. J. Millar, ed., Miscellaneous Scientific Papers: by W. J. Macquorn Rankine, ... (London, England: Charles Griffin and Co., 1881), part II, pages 203-208: "The law of the Conservation of Energy is already known—viz. that the sum of all the energies of the universe, actual and potential, is unchangeable."
- ↑ Hadden, Richard W. (1994). On the shoulders of merchants: exchange and the mathematical conception of nature in early modern Europe. SUNY Press. p. 13. ISBN 978-0-7914-2011-9. https://books.google.com/books?id=7IxtC4Jw1YoC., Chapter 1, p. 13
- ↑ Jensen, Carsten (2000). Controversy and Consensus: Nuclear Beta Decay 1911-1934. Birkhäuser Verlag. ISBN 978-3-7643-5313-1. https://www.springer.com/birkhauser/physics/book/978-3-7643-5313-1.
- ↑ Brown, Laurie M. (1978). "The idea of the neutrino". Physics Today 31 (9): 23–8. doi:10.1063/1.2995181. Bibcode: 1978PhT....31i..23B.
- ↑ Wilson, F. L. (1968). "Fermi's Theory of Beta Decay". American Journal of Physics 36 (12): 1150–1160. doi:10.1119/1.1974382. Bibcode: 1968AmJPh..36.1150W. http://microboone-docdb.fnal.gov/cgi-bin/RetrieveFile?docid=953;filename=FermiBetaDecay1934.pdf;version=1.
- ↑ Griffiths, D. (2009). Introduction to Elementary Particles (2nd ed.). pp. 314–315. ISBN 978-3-527-40601-2.
- ↑ Knuiman, Jan T.; Barneveld, Peter A.; Besseling, Nicolaas A. M. (2012). "On the Relation between the Fundamental Equation of Thermodynamics and the Energy Balance Equation in the Context of Closed and Open Systems". Journal of Chemical Education 89 (8): 968–972. doi:10.1021/ed200405k. Bibcode: 2012JChEd..89..968K. https://pubs.acs.org/doi/full/10.1021/ed200405k.
- ↑ Hanc, J., Tuleja, S., & Hancova, M. (2004). Symmetries and conservation laws: Consequences of Noether’s theorem. American Journal of Physics, 72(4), 428-435.
- ↑ Harrison, E. R. (1995). Mining energy in an expanding universe. The Astrophysical Journal, 446, 63.
- ↑ Tamara M. Davis (2010). "Is the Universe Leaking Energy?". Scientific American. https://www.scientificamerican.com/article/is-the-universe-leaking-energy/.
- ↑ "Is Energy Conserved in General Relativity?". http://math.ucr.edu/home/baez/physics/Relativity/GR/energy_gr.html.
- ↑ Duerr, Patrick M. (February 2019). "Fantastic Beasts and where (not) to find them: Local gravitational energy and energy conservation in general relativity". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 65: 1–14. doi:10.1016/j.shpsb.2018.07.002. Bibcode: 2019SHPMP..65....1D.
- ↑ Moskowitz, Clara (2014). "Fact or Fiction?: Energy Can Neither Be Created Nor Destroyed" (in en). Scientific American. https://www.scientificamerican.com/article/energy-can-neither-be-created-nor-destroyed/.
- ↑ "Confronting the Multiverse: What 'Infinite Universes' Would Mean" (in en). Space.com. 23 December 2015. https://www.space.com/31465-is-our-universe-just-one-of-many-in-a-multiverse.html.
- ↑ "Puzzling Quantum Scenario Appears Not to Conserve Energy". Quanta Magazine. 2022. https://www.quantamagazine.org/puzzling-quantum-scenario-appears-not-to-conserve-energy-20220516/.
- ↑ 30.0 30.1 Carroll, Sean M.; Lodman, Jackie (August 2021). "Energy Non-conservation in Quantum Mechanics". Foundations of Physics 51 (4): 83. doi:10.1007/s10701-021-00490-5. Bibcode: 2021FoPh...51...83C.
- ↑ "The perpetual myth of free energy". BBC. 9 July 2007. http://news.bbc.co.uk/2/hi/technology/6283374.stm.
- ↑ Maudlin, Tim; Okon, Elias; Sudarsky, Daniel (February 2020). "On the status of conservation laws in physics: Implications for semiclassical gravity". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 69: 67–81. doi:10.1016/j.shpsb.2019.10.004. Bibcode: 2020SHPMP..69...67M.
- ↑ Amelino-Camelia, Giovanni (12 June 2013). "Quantum-Spacetime Phenomenology". Living Reviews in Relativity 16 (1): 5. doi:10.12942/lrr-2013-5. PMID 28179844. Bibcode: 2013LRR....16....5A.
- ↑ Carlesso, Matteo; Donadi, Sandro; Ferialdi, Luca; Paternostro, Mauro; Ulbricht, Hendrik; Bassi, Angelo (March 2022). "Present status and future challenges of non-interferometric tests of collapse models". Nature Physics 18 (3): 243–250. doi:10.1038/s41567-021-01489-5. Bibcode: 2022NatPh..18..243C.
Bibliography
Modern accounts
- Goldstein, Martin, and Inge F., (1993). The Refrigerator and the Universe. Harvard Univ. Press. A gentle introduction.
- Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 978-0-7167-1088-2.
- Nolan, Peter J. (1996). Fundamentals of College Physics, 2nd ed.. William C. Brown Publishers.
- Oxtoby & Nachtrieb (1996). Principles of Modern Chemistry, 3rd ed.. Saunders College Publishing.
- Papineau, D. (2002). Thinking about Consciousness. Oxford: Oxford University Press.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 978-0-534-40842-8. https://archive.org/details/physicssciengv2p00serw.
- Stenger, Victor J. (2000). Timeless Reality. Prometheus Books. Especially chpt. 12. Nontechnical.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 978-0-7167-0809-4.
- Lanczos, Cornelius (1970). The Variational Principles of Mechanics. Toronto: University of Toronto Press. ISBN 978-0-8020-1743-7.
History of ideas
- Brown, T.M. (1965). "Resource letter EEC-1 on the evolution of energy concepts from Galileo to Helmholtz". American Journal of Physics 33 (10): 759–765. doi:10.1119/1.1970980. Bibcode: 1965AmJPh..33..759B.
- Cardwell, D.S.L. (1971). From Watt to Clausius: The Rise of Thermodynamics in the Early Industrial Age. London: Heinemann. ISBN 978-0-435-54150-7.
- Guillen, M. (1999). Five Equations That Changed the World. New York: Abacus. ISBN 978-0-349-11064-6.
- Hiebert, E.N. (1981). Historical Roots of the Principle of Conservation of Energy. Madison, Wis.: Ayer Co Pub. ISBN 978-0-405-13880-5.
- Kuhn, T.S. (1957) "Energy conservation as an example of simultaneous discovery", in M. Clagett (ed.) Critical Problems in the History of Science pp.321–56
- Sarton, G.; Joule, J. P.; Carnot, Sadi (1929). "The discovery of the law of conservation of energy". Isis 13: 18–49. doi:10.1086/346430.
- Smith, C. (1998). The Science of Energy: Cultural History of Energy Physics in Victorian Britain. London: Heinemann. ISBN 978-0-485-11431-7.
- Mach, E. (1872). History and Root of the Principles of the Conservation of Energy. Open Court Pub. Co., Illinois. https://archive.org/details/historyandrootp00machgoog.
- Poincaré, H. (1905). Science and Hypothesis. Walter Scott Publishing Co. Ltd; Dover reprint, 1952. ISBN 978-0-486-60221-9. https://archive.org/details/scienceandhypoth00poinuoft., Chapter 8, "Energy and Thermo-dynamics"
External links
- MISN-0-158 The First Law of Thermodynamics (PDF file) by Jerzy Borysowicz for Project PHYSNET.
 |

