Bernoulli's triangle

Short description: Array of partial sums of the binomial coefficients

Derivation of Bernoulli's triangle (blue bold text) from Pascal's triangle (pink italics)

Bernoulli's triangle is an array of partial sums of the binomial coefficients. For any non-negative integer n and for any integer k included between 0 and n, the component in row n and column k is given by:

[math]\displaystyle{ \sum_{p=0}^k {n \choose p}, }[/math]

As the numbers of com­po­si­tions of n +1 into k +1 ordered partitions form Pascal's triangle, the numbers of compositions of n +1 into k +1 or fewer ordered partitions form Bernoulli's triangle

i.e., the sum of the first k nth-order binomial coefficients. The first rows of Bernoulli's triangle are:

[math]\displaystyle{ \begin{array}{cc|cccccc} & k & 0 & 1 & 2 & 3 & 4 & 5\\ n & & \\ \hline 0 & & 1 \\ 1 & & 1 & 2 \\ 2 & & 1 & 3 & 4 \\ 3 & & 1 & 4 & 7 & 8 \\ 4 & & 1 & 5 & 11 & 15 & 16 \\ 5 & & 1 & 6 & 16 & 26 & 31 & 32 \end{array} }[/math]

Similarly to Pascal's triangle, each component of Bernoulli's triangle is the sum of two components of the previous row, except for the last number of each row, which is double the last number of the previous row. For example, if [math]\displaystyle{ B_{n,k} }[/math] denotes the component in row n and column k, then:

[math]\displaystyle{ B_{n,k}=\begin{cases} 1 & \mbox{if } n=0 \\ B_{n-1,k}+B_{n-1,k-1} & \mbox{if } k\lt n \\ 2B_{n-1,k-1} = 2^n & \mbox{if } k=n \end{cases} }[/math]

Sequences derived from the Bernoulli triangle

Sequences from the On-Line Encyclopedia of Integer Sequences in Bernoulli's triangle

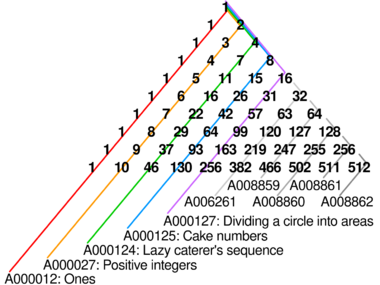
As in Pascal's triangle and other similarly constructed triangles, sums of components along diagonal paths in Bernoulli's triangle result in the Fibonacci numbers.

As the third column of Bernoulli's triangle (k = 2) is a triangular number plus one, it forms the lazy caterer's sequence for n cuts, where n ≥ 2. The fourth column (k = 3) is the three-dimensional analogue, known as the cake numbers, for n cuts, where n ≥ 3.

The fifth column (k = 4) gives the maximum number of regions in the problem of dividing a circle into areas for n + 1 points, where n ≥ 4.

In general, the (k + 1)th column gives the maximum number of regions in k-dimensional space formed by n − 1 (k − 1)-dimensional hyperplanes, for n ≥ k. It also gives the number of compositions (ordered partitions) of n + 1 into k + 1 or fewer parts.

External links

• The sequence of numbers formed by Bernoulli's triangle on the On-Line Encyclopedia of Integer Sequences: https://oeis.org/A008949.