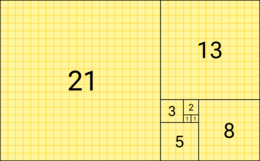
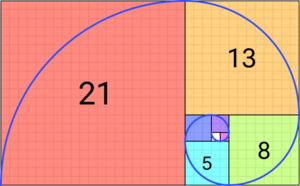
Fibonacci number

In mathematics, the Fibonacci numbers, commonly denoted Fn , form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes (as did Fibonacci) from 1 and 2. Starting from 0 and 1, the first few values in the sequence are:[1]
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.
The Fibonacci numbers were first described in Indian mathematics,[2][3][4] as early as 200 BC in work by Pingala on enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths. They are named after the Italian mathematician Leonardo of Pisa, later known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book Liber Abaci.[5]
Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the Fibonacci Quarterly. Applications of Fibonacci numbers include computer algorithms such as the Fibonacci search technique and the Fibonacci heap data structure, and graphs called Fibonacci cubes used for interconnecting parallel and distributed systems. They also appear in biological settings, such as branching in trees, the arrangement of leaves on a stem, the fruit sprouts of a pineapple, the flowering of an artichoke, an uncurling fern, and the arrangement of a pine cone's bracts.
Fibonacci numbers are also strongly related to the golden ratio: Binet's formula expresses the nth Fibonacci number in terms of n and the golden ratio, and implies that the ratio of two consecutive Fibonacci numbers tends to the golden ratio as n increases. Fibonacci numbers are also closely related to Lucas numbers, which obey the same recurrence relation and with the Fibonacci numbers form a complementary pair of Lucas sequences.
Definition
The Fibonacci numbers may be defined by the recurrence relation[6] and for n > 1.
Under some older definitions, the value is omitted, so that the sequence starts with and the recurrence is valid for n > 2.[7][8]
The first 20 Fibonacci numbers Fn are:[1]
F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15 F16 F17 F18 F19 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181
History
India
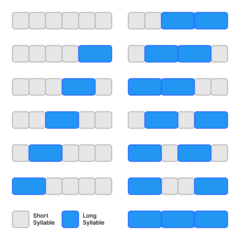
The Fibonacci sequence appears in Indian mathematics, in connection with Sanskrit prosody.[3][9][10] In the Sanskrit poetic tradition, there was interest in enumerating all patterns of long (L) syllables of 2 units duration, juxtaposed with short (S) syllables of 1 unit duration. Counting the different patterns of successive L and S with a given total duration results in the Fibonacci numbers: the number of patterns of duration m units is Fm+1.[4]
Knowledge of the Fibonacci sequence was expressed as early as Pingala (c. 450 BC–200 BC). Singh cites Pingala's cryptic formula misrau cha ("the two are mixed") and scholars who interpret it in context as saying that the number of patterns for m beats (Fm+1) is obtained by adding one [S] to the Fm cases and one [L] to the Fm−1 cases.[11] Bharata Muni also expresses knowledge of the sequence in the Natya Shastra (c. 100 BC–c. 350 AD).[12][2] However, the clearest exposition of the sequence arises in the work of Virahanka (c. 700 AD), whose own work is lost, but is available in a quotation by Gopala (c. 1135):[10]
Variations of two earlier meters [is the variation]... For example, for [a meter of length] four, variations of meters of two [and] three being mixed, five happens. [works out examples 8, 13, 21]... In this way, the process should be followed in all mātrā-vṛttas [prosodic combinations].[lower-alpha 1]
Hemachandra (c. 1150) is credited with knowledge of the sequence as well,[2] writing that "the sum of the last and the one before the last is the number ... of the next mātrā-vṛtta."[14][15]
Europe

the indices from present to XII (months) as Latin ordinals and Roman numerals and the numbers (of rabbit pairs) as Hindu-Arabic numerals starting with 1, 2, 3, 5 and ending with 377.
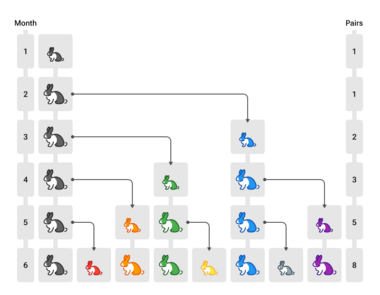
The Fibonacci sequence first appears in the book Liber Abaci (The Book of Calculation, 1202) by Fibonacci[16][17] where it is used to calculate the growth of rabbit populations.[18][19] Fibonacci considers the growth of an idealized (biologically unrealistic) rabbit population, assuming that: a newly born breeding pair of rabbits are put in a field; each breeding pair mates at the age of one month, and at the end of their second month they always produce another pair of rabbits; and rabbits never die, but continue breeding forever. Fibonacci posed the puzzle: how many pairs will there be in one year?
- At the end of the first month, they mate, but there is still only 1 pair.
- At the end of the second month they produce a new pair, so there are 2 pairs in the field.
- At the end of the third month, the original pair produce a second pair, but the second pair only mate to gestate for a month, so there are 3 pairs in all.
- At the end of the fourth month, the original pair has produced yet another new pair, and the pair born two months ago also produces their first pair, making 5 pairs.
At the end of the nth month, the number of pairs of rabbits is equal to the number of mature pairs (that is, the number of pairs in month n – 2) plus the number of pairs alive last month (month n – 1). The number in the nth month is the nth Fibonacci number.[20]
The name "Fibonacci sequence" was first used by the 19th-century number theorist Édouard Lucas.[21]
Relation to the golden ratio
Closed-form expression
Like every sequence defined by a linear recurrence with constant coefficients, the Fibonacci numbers have a closed-form expression. It has become known as Binet's formula, named after French mathematician Jacques Philippe Marie Binet, though it was already known by Abraham de Moivre and Daniel Bernoulli:[22]
where is the golden ratio, and ψ is its conjugate:[23]
Since , this formula can also be written as
To see the relation between the sequence and these constants,[24] note that φ and ψ are both solutions of the equation so the powers of φ and ψ satisfy the Fibonacci recursion. In other words,
- and
It follows that for any values a and b, the sequence defined by satisfies the same recurrence.
If a and b are chosen so that U0 = 0 and U1 = 1 then the resulting sequence Un must be the Fibonacci sequence. This is the same as requiring a and b satisfy the system of equations: which has solution producing the required formula.
Taking the starting values U0 and U1 to be arbitrary constants, a more general solution is: where
Computation by rounding
Since
for all n ≥ 0, the number Fn is the closest integer to . Therefore, it can be found by rounding, using the nearest integer function:
In fact, the rounding error is very small, being less than 0.1 for n ≥ 4, and less than 0.01 for n ≥ 8.
Fibonacci numbers can also be computed by truncation, in terms of the floor function:
As the floor function is monotonic, the latter formula can be inverted for finding the index n(F ) of the smallest Fibonacci number that is not less than a positive integer F: where , ,[25] and .[26]
Magnitude
Since Fn is asymptotic to , the number of digits in Fn is asymptotic to . As a consequence, for every integer d > 1 there are either 4 or 5 Fibonacci numbers with d decimal digits.
More generally, in the base b representation, the number of digits in Fn is asymptotic to
Limit of consecutive quotients
Johannes Kepler observed that the ratio of consecutive Fibonacci numbers converges. He wrote that "as 5 is to 8 so is 8 to 13, practically, and as 8 is to 13, so is 13 to 21 almost", and concluded that these ratios approach the golden ratio [27][28]
This convergence holds regardless of the starting values and , unless . This can be verified using Binet's formula. For example, the initial values 3 and 2 generate the sequence 3, 2, 5, 7, 12, 19, 31, 50, 81, 131, 212, 343, 555, ... . The ratio of consecutive terms in this sequence shows the same convergence towards the golden ratio.
In general, , because the ratios between consecutive Fibonacci numbers approaches .

Successive tilings of the plane and a graph of approximations to the golden ratio calculated by dividing each Fibonacci number by the previous
Decomposition of powers
Since the golden ratio satisfies the equation
this expression can be used to decompose higher powers as a linear function of lower powers, which in turn can be decomposed all the way down to a linear combination of and 1. The resulting recurrence relationships yield Fibonacci numbers as the linear coefficients: This equation can be proved by induction on n ≥ 1: For , it is also the case that and it is also the case that
These expressions are also true for n < 1 if the Fibonacci sequence Fn is extended to negative integers using the Fibonacci rule
Identification
Binet's formula provides a proof that a positive integer x is a Fibonacci number if and only if at least one of or is a perfect square.[29] This is because Binet's formula, which can be written as , can be multiplied by and solved as a quadratic equation in via the quadratic formula:
Comparing this to , it follows that
In particular, the left-hand side is a perfect square.
Matrix form
A 2-dimensional system of linear difference equations that describes the Fibonacci sequence is
alternatively denoted
which yields . The eigenvalues of the matrix A are and corresponding to the respective eigenvectors and As the initial value is it follows that the nth term is From this, the nth element in the Fibonacci series may be read off directly as a closed-form expression:
Equivalently, the same computation may be performed by diagonalization of A through use of its eigendecomposition: where and The closed-form expression for the nth element in the Fibonacci series is therefore given by
which again yields
The matrix A has a determinant of −1, and thus it is a 2 × 2 unimodular matrix.
This property can be understood in terms of the continued fraction representation for the golden ratio:
The Fibonacci numbers occur as the ratio of successive convergents of the continued fraction for φ, and the matrix formed from successive convergents of any continued fraction has a determinant of +1 or −1. The matrix representation gives the following closed-form expression for the Fibonacci numbers:
For a given n, this matrix can be computed in O(log(n)) arithmetic operations, using the exponentiation by squaring method.
Taking the determinant of both sides of this equation yields Cassini's identity,
Moreover, since AnAm = An+m for any square matrix A, the following identities can be derived (they are obtained from two different coefficients of the matrix product, and one may easily deduce the second one from the first one by changing n into n + 1),
In particular, with m = n,
These last two identities provide a way to compute Fibonacci numbers recursively in O(log(n)) arithmetic operations and in time O(M(n) log(n)), where M(n) is the time for the multiplication of two numbers of n digits. This matches the time for computing the nth Fibonacci number from the closed-form matrix formula, but with fewer redundant steps if one avoids recomputing an already computed Fibonacci number (recursion with memoization).[30]
Combinatorial identities
Combinatorial proofs
Most identities involving Fibonacci numbers can be proved using combinatorial arguments using the fact that can be interpreted as the number of (possibly empty) sequences of 1s and 2s whose sum is . This can be taken as the definition of with the conventions , meaning no such sequence exists whose sum is −1, and , meaning the empty sequence "adds up" to 0. In the following, is the cardinality of a set:
In this manner the recurrence relation may be understood by dividing the sequences into two non-overlapping sets where all sequences either begin with 1 or 2: Excluding the first element, the remaining terms in each sequence sum to or and the cardinality of each set is or giving a total of sequences, showing this is equal to .
In a similar manner it may be shown that the sum of the first Fibonacci numbers up to the nth is equal to the (n + 2)nd Fibonacci number minus 1.[31] In symbols:
This may be seen by dividing all sequences summing to based on the location of the first 2. Specifically, each set consists of those sequences that start until the last two sets each with cardinality 1.
Following the same logic as before, by summing the cardinality of each set we see that
... where the last two terms have the value . From this it follows that .
A similar argument, grouping the sums by the position of the first 1 rather than the first 2 gives two more identities: and In words, the sum of the first Fibonacci numbers with odd index up to is the (2n)th Fibonacci number, and the sum of the first Fibonacci numbers with even index up to is the (2n + 1)st Fibonacci number minus 1.[32]
A different trick may be used to prove or in words, the sum of the squares of the first Fibonacci numbers up to is the product of the nth and (n + 1)st Fibonacci numbers. To see this, begin with a Fibonacci rectangle of size and decompose it into squares of size ; from this the identity follows by comparing areas:
Symbolic method
The sequence is also considered using the symbolic method.[33] More precisely, this sequence corresponds to a specifiable combinatorial class. The specification of this sequence is . Indeed, as stated above, the -th Fibonacci number equals the number of combinatorial compositions (ordered partitions) of using terms 1 and 2.
It follows that the ordinary generating function of the Fibonacci sequence, i.e. , is the complex function
Induction proofs
Fibonacci identities often can be easily proved using mathematical induction.
For example, reconsider Adding to both sides gives
and so we have the formula for
Similarly, add to both sides of to give
Binet formula proofs
The Binet formula is This can be used to prove Fibonacci identities.
For example, to prove that note that the left hand side multiplied by becomes as required, using the facts and to simplify the equations.
Other identities
Numerous other identities can be derived using various methods. Here are some of them:[34]
Cassini's and Catalan's identities
Cassini's identity states that Catalan's identity is a generalization:
d'Ocagne's identity
where Ln is the n-th Lucas number. The last is an identity for doubling n; other identities of this type are by Cassini's identity.
These can be found experimentally using lattice reduction, and are useful in setting up the special number field sieve to factorize a Fibonacci number.
More generally,[34]
or alternatively
Putting k = 2 in this formula, one gets again the formulas of the end of above section Matrix form.
Generating function
The generating function of the Fibonacci sequence is the power series
This series is convergent for and its sum has a simple closed-form:[35]
This can be proved by using the Fibonacci recurrence to expand each coefficient in the infinite sum:
Solving the equation for results in the closed form.
The partial fraction decomposition is given by where is the golden ratio and is its conjugate.
gives the generating function for the negafibonacci numbers, and satisfies the functional equation
Reciprocal sums
Infinite sums over reciprocal Fibonacci numbers can sometimes be evaluated in terms of theta functions. For example, the sum of every odd-indexed reciprocal Fibonacci number can be written as
and the sum of squared reciprocal Fibonacci numbers as
If we add 1 to each Fibonacci number in the first sum, there is also the closed form
and there is a nested sum of squared Fibonacci numbers giving the reciprocal of the golden ratio,
The sum of all even-indexed reciprocal Fibonacci numbers is[36] with the Lambert series since
So the reciprocal Fibonacci constant is[37]
Moreover, this number has been proved irrational by Richard André-Jeannin.[38]
Millin's series gives the identity[39] which follows from the closed form for its partial sums as N tends to infinity:
Primes and divisibility
Divisibility properties
Every third number of the sequence is even (a multiple of ) and, more generally, every kth number of the sequence is a multiple of Fk. Thus the Fibonacci sequence is an example of a divisibility sequence. In fact, the Fibonacci sequence satisfies the stronger divisibility property[40][41] where gcd is the greatest common divisor function.
In particular, any three consecutive Fibonacci numbers are pairwise coprime because both and . That is,
for every n.
Every prime number p divides a Fibonacci number that can be determined by the value of p modulo 5. If p is congruent to 1 or 4 modulo 5, then p divides Fp−1, and if p is congruent to 2 or 3 modulo 5, then, p divides Fp+1. The remaining case is that p = 5, and in this case p divides Fp.
These cases can be combined into a single, non-piecewise formula, using the Legendre symbol:[42]
Primality testing
The above formula can be used as a primality test in the sense that if where the Legendre symbol has been replaced by the Jacobi symbol, then this is evidence that n is a prime, and if it fails to hold, then n is definitely not a prime. If n is composite and satisfies the formula, then n is a Fibonacci pseudoprime. When m is large – say a 500-bit number – then we can calculate Fm (mod n) efficiently using the matrix form. Thus
Here the matrix power Am is calculated using modular exponentiation, which can be adapted to matrices.[43]
Fibonacci primes
A Fibonacci prime is a Fibonacci number that is prime. The first few are:[44]
- 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, ...
Fibonacci primes with thousands of digits have been found, but it is not known whether there are infinitely many.[45]
Fkn is divisible by Fn, so, apart from F4 = 3, any Fibonacci prime must have a prime index. As there are arbitrarily long runs of composite numbers, there are therefore also arbitrarily long runs of composite Fibonacci numbers.
No Fibonacci number greater than F6 = 8 is one greater or one less than a prime number.[46]
The only nontrivial square Fibonacci number is 144.[47] Attila Pethő proved in 2001 that there is only a finite number of perfect power Fibonacci numbers.[48] In 2006, Y. Bugeaud, M. Mignotte, and S. Siksek proved that 8 and 144 are the only such non-trivial perfect powers.[49]
1, 3, 21, and 55 are the only triangular Fibonacci numbers, which was conjectured by Vern Hoggatt and proved by Luo Ming.[50]
No Fibonacci number can be a perfect number.[51] More generally, no Fibonacci number other than 1 can be multiply perfect,[52] and no ratio of two Fibonacci numbers can be perfect.[53]
Prime divisors
With the exceptions of 1, 8 and 144 (F1 = F2, F6 and F12) every Fibonacci number has a prime factor that is not a factor of any smaller Fibonacci number (Carmichael's theorem).[54] As a result, 8 and 144 (F6 and F12) are the only Fibonacci numbers that are the product of other Fibonacci numbers.[55]
The divisibility of Fibonacci numbers by a prime p is related to the Legendre symbol which is evaluated as follows:
If p is a prime number then [56][57]
For example,
It is not known whether there exists a prime p such that
Such primes (if there are any) would be called Wall–Sun–Sun primes.
Also, if p ≠ 5 is an odd prime number then:[58]
Example 1. p = 7, in this case p ≡ 3 (mod 4) and we have:
Example 2. p = 11, in this case p ≡ 3 (mod 4) and we have:
Example 3. p = 13, in this case p ≡ 1 (mod 4) and we have:
Example 4. p = 29, in this case p ≡ 1 (mod 4) and we have:
For odd n, all odd prime divisors of Fn are congruent to 1 modulo 4, implying that all odd divisors of Fn (as the products of odd prime divisors) are congruent to 1 modulo 4.[59]
For example,
All known factors of Fibonacci numbers F(i ) for all i < 50000 are collected at the relevant repositories.[60][61]
Periodicity modulo n
If the members of the Fibonacci sequence are taken mod n, the resulting sequence is periodic with period at most 6n.[62] The lengths of the periods for various n form the so-called Pisano periods.[63] Determining a general formula for the Pisano periods is an open problem, which includes as a subproblem a special instance of the problem of finding the multiplicative order of a modular integer or of an element in a finite field. However, for any particular n, the Pisano period may be found as an instance of cycle detection.
Generalizations
The Fibonacci sequence is one of the simplest and earliest known sequences defined by a recurrence relation, and specifically by a linear difference equation. All these sequences may be viewed as generalizations of the Fibonacci sequence. In particular, Binet's formula may be generalized to any sequence that is a solution of a homogeneous linear difference equation with constant coefficients.
Some specific examples that are close, in some sense, to the Fibonacci sequence include:
- Generalizing the index to negative integers to produce the negafibonacci numbers.
- Generalizing the index to real numbers using a modification of Binet's formula.[34]
- Starting with other integers. Lucas numbers have L1 = 1, L2 = 3, and Ln = Ln−1 + Ln−2. Primefree sequences use the Fibonacci recursion with other starting points to generate sequences in which all numbers are composite.
- Letting a number be a linear function (other than the sum) of the 2 preceding numbers. The Pell numbers have Pn = 2Pn−1 + Pn−2. If the coefficient of the preceding value is assigned a variable value x, the result is the sequence of Fibonacci polynomials.
- Not adding the immediately preceding numbers. The Padovan sequence and Perrin numbers have P(n) = P(n − 2) + P(n − 3).
- Generating the next number by adding 3 numbers (tribonacci numbers), 4 numbers (tetranacci numbers), or more. The resulting sequences are known as n-Step Fibonacci numbers.[64]
Applications
Mathematics

The Fibonacci numbers occur in the sums of "shallow" diagonals in Pascal's triangle (see Binomial coefficient):[65]
The generating function can be expanded into and collecting like terms of , we have the identity
To see how the formula is used, we can arrange the sums by the number of terms present:
5 = 1+1+1+1+1 = 2+1+1+1 = 1+2+1+1 = 1+1+2+1 = 1+1+1+2 = 2+2+1 = 2+1+2 = 1+2+2
which is , where we are choosing the positions of k twos from n−k−1 terms.
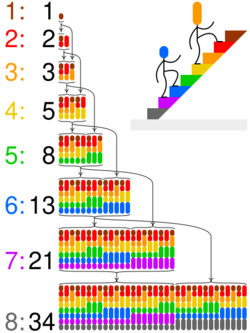
These numbers also give the solution to certain enumerative problems,[66] the most common of which is that of counting the number of ways of writing a given number n as an ordered sum of 1s and 2s (called compositions); there are Fn+1 ways to do this (equivalently, it's also the number of domino tilings of the rectangle). For example, there are F5+1 = F6 = 8 ways one can climb a staircase of 5 steps, taking one or two steps at a time:
5 = 1+1+1+1+1 = 2+1+1+1 = 1+2+1+1 = 1+1+2+1 = 2+2+1 = 1+1+1+2 = 2+1+2 = 1+2+2
The figure shows that 8 can be decomposed into 5 (the number of ways to climb 4 steps, followed by a single-step) plus 3 (the number of ways to climb 3 steps, followed by a double-step). The same reasoning is applied recursively until a single step, of which there is only one way to climb.
The Fibonacci numbers can be found in different ways among the set of binary strings, or equivalently, among the subsets of a given set.
- The number of binary strings of length n without consecutive 1s is the Fibonacci number Fn+2. For example, out of the 16 binary strings of length 4, there are F6 = 8 without consecutive 1s – they are 0000, 0001, 0010, 0100, 0101, 1000, 1001, and 1010. Such strings are the binary representations of Fibbinary numbers. Equivalently, Fn+2 is the number of subsets S of {1, ..., n} without consecutive integers, that is, those S for which {i, i + 1} ⊈ S for every i. A bijection with the sums to n+1 is to replace 1 with 0 and 2 with 10, and drop the last zero.
- The number of binary strings of length n without an odd number of consecutive 1s is the Fibonacci number Fn+1. For example, out of the 16 binary strings of length 4, there are F5 = 5 without an odd number of consecutive 1s – they are 0000, 0011, 0110, 1100, 1111. Equivalently, the number of subsets S of {1, ..., n} without an odd number of consecutive integers is Fn+1. A bijection with the sums to n is to replace 1 with 0 and 2 with 11.
- The number of binary strings of length n without an even number of consecutive 0s or 1s is 2Fn. For example, out of the 16 binary strings of length 4, there are 2F4 = 6 without an even number of consecutive 0s or 1s – they are 0001, 0111, 0101, 1000, 1010, 1110. There is an equivalent statement about subsets.
- Yuri Matiyasevich was able to show that the Fibonacci numbers can be defined by a Diophantine equation, which led to his solving Hilbert's tenth problem.[67]
- The Fibonacci numbers are also an example of a complete sequence. This means that every positive integer can be written as a sum of Fibonacci numbers, where any one number is used once at most.
- Moreover, every positive integer can be written in a unique way as the sum of one or more distinct Fibonacci numbers in such a way that the sum does not include any two consecutive Fibonacci numbers. This is known as Zeckendorf's theorem, and a sum of Fibonacci numbers that satisfies these conditions is called a Zeckendorf representation. The Zeckendorf representation of a number can be used to derive its Fibonacci coding.
- Starting with 5, every second Fibonacci number is the length of the hypotenuse of a right triangle with integer sides, or in other words, the largest number in a Pythagorean triple, obtained from the formula The sequence of Pythagorean triangles obtained from this formula has sides of lengths (3,4,5), (5,12,13), (16,30,34), (39,80,89), ... . The middle side of each of these triangles is the sum of the three sides of the preceding triangle.[68]
- The Fibonacci cube is an undirected graph with a Fibonacci number of nodes that has been proposed as a network topology for parallel computing.
- Fibonacci numbers appear in the ring lemma, used to prove connections between the circle packing theorem and conformal maps.[69]
Computer science

The keys in the left spine are Fibonacci numbers.
- The Fibonacci numbers are important in computational run-time analysis of Euclid's algorithm to determine the greatest common divisor of two integers: the worst case input for this algorithm is a pair of consecutive Fibonacci numbers.[70]
- Fibonacci numbers are used in a polyphase version of the merge sort algorithm in which an unsorted list is divided into two lists whose lengths correspond to sequential Fibonacci numbers – by dividing the list so that the two parts have lengths in the approximate proportion φ. A tape-drive implementation of the polyphase merge sort was described in The Art of Computer Programming.
- A Fibonacci tree is a binary tree whose child trees (recursively) differ in height by exactly 1. So it is an AVL tree, and one with the fewest nodes for a given height — the "thinnest" AVL tree. These trees have a number of vertices that is a Fibonacci number minus one, an important fact in the analysis of AVL trees.[71]
- Fibonacci numbers are used by some pseudorandom number generators.
- Fibonacci numbers arise in the analysis of the Fibonacci heap data structure.
- A one-dimensional optimization method, called the Fibonacci search technique, uses Fibonacci numbers.[72]
- The Fibonacci number series is used for optional lossy compression in the IFF 8SVX audio file format used on Amiga computers. The number series compands the original audio wave similar to logarithmic methods such as μ-law.[73][74]
- Some Agile teams use a modified series called the "Modified Fibonacci Series" in planning poker, as an estimation tool. Planning Poker is a formal part of the Scaled Agile Framework.[75]
- Fibonacci coding
- Negafibonacci coding
Nature

Fibonacci sequences appear in biological settings,[76] such as branching in trees, arrangement of leaves on a stem, the fruitlets of a pineapple,[77] the flowering of artichoke, an uncurling fern and the arrangement of a pine cone,[78] and the family tree of honeybees.[79][80] Kepler pointed out the presence of the Fibonacci sequence in nature, using it to explain the (golden ratio-related) pentagonal form of some flowers.[81] Field daisies most often have petals in counts of Fibonacci numbers.[82] In 1830, K. F. Schimper and A. Braun discovered that the parastichies (spiral phyllotaxis) of plants were frequently expressed as fractions involving Fibonacci numbers.[83]
Przemysław Prusinkiewicz advanced the idea that real instances can in part be understood as the expression of certain algebraic constraints on free groups, specifically as certain Lindenmayer grammars.[84]

A model for the pattern of florets in the head of a sunflower was proposed by Helmut Vogel (de) in 1979.[85] This has the form
where n is the index number of the floret and c is a constant scaling factor; the florets thus lie on Fermat's spiral. The divergence angle, approximately 137.51°, is the golden angle, dividing the circle in the golden ratio. Because this ratio is irrational, no floret has a neighbor at exactly the same angle from the center, so the florets pack efficiently. Because the rational approximations to the golden ratio are of the form F( j):F( j + 1), the nearest neighbors of floret number n are those at n ± F( j) for some index j, which depends on r, the distance from the center. Sunflowers and similar flowers most commonly have spirals of florets in clockwise and counter-clockwise directions in the amount of adjacent Fibonacci numbers,[86] typically counted by the outermost range of radii.[87]
Fibonacci numbers also appear in the pedigrees of idealized honeybees, according to the following rules:
- If an egg is laid by an unmated female, it hatches a male or drone bee.
- If, however, an egg was fertilized by a male, it hatches a female.
Thus, a male bee always has one parent, and a female bee has two. If one traces the pedigree of any male bee (1 bee), he has 1 parent (1 bee), 2 grandparents, 3 great-grandparents, 5 great-great-grandparents, and so on. This sequence of numbers of parents is the Fibonacci sequence. The number of ancestors at each level, Fn, is the number of female ancestors, which is Fn−1, plus the number of male ancestors, which is Fn−2.[88] This is under the unrealistic assumption that the ancestors at each level are otherwise unrelated.

It has been noticed that the number of possible ancestors on the human X chromosome inheritance line at a given ancestral generation also follows the Fibonacci sequence.[89] A male individual has an X chromosome, which he received from his mother, and a Y chromosome, which he received from his father. The male counts as the "origin" of his own X chromosome (), and at his parents' generation, his X chromosome came from a single parent (). The male's mother received one X chromosome from her mother (the son's maternal grandmother), and one from her father (the son's maternal grandfather), so two grandparents contributed to the male descendant's X chromosome (). The maternal grandfather received his X chromosome from his mother, and the maternal grandmother received X chromosomes from both of her parents, so three great-grandparents contributed to the male descendant's X chromosome (). Five great-great-grandparents contributed to the male descendant's X chromosome (), etc. (This assumes that all ancestors of a given descendant are independent, but if any genealogy is traced far enough back in time, ancestors begin to appear on multiple lines of the genealogy, until eventually a population founder appears on all lines of the genealogy.)
Other
- In optics, when a beam of light shines at an angle through two stacked transparent plates of different materials of different refractive indexes, it may reflect off three surfaces: the top, middle, and bottom surfaces of the two plates. The number of different beam paths that have k reflections, for k > 1, is the th Fibonacci number. (However, when k = 1, there are three reflection paths, not two, one for each of the three surfaces.)[90]
- Fibonacci retracement levels are widely used in technical analysis for financial market trading.
- Since the conversion factor 1.609344 for miles to kilometers is close to the golden ratio, the decomposition of distance in miles into a sum of Fibonacci numbers becomes nearly the kilometer sum when the Fibonacci numbers are replaced by their successors. This method amounts to a radix 2 number register in golden ratio base φ being shifted. To convert from kilometers to miles, shift the register down the Fibonacci sequence instead.[91]
- The measured values of voltages and currents in the infinite resistor chain circuit (also called the resistor ladder or infinite series-parallel circuit) follow the Fibonacci sequence. The intermediate results of adding the alternating series and parallel resistances yields fractions composed of consecutive Fibonacci numbers. The equivalent resistance of the entire circuit equals the golden ratio.[92]
- Brasch et al. 2012 show how a generalized Fibonacci sequence also can be connected to the field of economics.[93] In particular, it is shown how a generalized Fibonacci sequence enters the control function of finite-horizon dynamic optimisation problems with one state and one control variable. The procedure is illustrated in an example often referred to as the Brock–Mirman economic growth model.
- Mario Merz included the Fibonacci sequence in some of his artworks beginning in 1970.[94]
- Joseph Schillinger (1895–1943) developed a system of composition which uses Fibonacci intervals in some of its melodies; he viewed these as the musical counterpart to the elaborate harmony evident within nature.[95] See also Golden ratio § Music.
See also
- Organization:The Fibonacci Association – Organization for research on Fibonacci numbers
- Social:Fibonacci numbers in popular culture
- Fibonacci word – Binary sequence from Fibonacci recurrence
- Random Fibonacci sequence – Randomized mathematical sequence based upon the Fibonacci sequence
- Wythoff array – Infinite matrix of integers derived from the Fibonacci sequence
References
Explanatory footnotes
- ↑ "For four, variations of meters of two [and] three being mixed, five happens. For five, variations of two earlier – three [and] four, being mixed, eight is obtained. In this way, for six, [variations] of four [and] of five being mixed, thirteen happens. And like that, variations of two earlier meters being mixed, seven morae [is] twenty-one. In this way, the process should be followed in all mātrā-vṛttas" [13]
Citations
- ↑ 1.0 1.1 Sloane, N. J. A., ed. "Sequence A000045". OEIS Foundation. https://oeis.org/A000045.
- ↑ 2.0 2.1 2.2 Goonatilake, Susantha (1998), Toward a Global Science, Indiana University Press, p. 126, ISBN 978-0-253-33388-9, https://books.google.com/books?id=SI5ip95BbgEC&pg=PA126
- ↑ 3.0 3.1 Singh, Parmanand (1985), "The So-called Fibonacci numbers in ancient and medieval India", Historia Mathematica 12 (3): 229–44, doi:10.1016/0315-0860(85)90021-7
- ↑ 4.0 4.1 Knuth, Donald (2006), The Art of Computer Programming, 4. Generating All Trees – History of Combinatorial Generation, Addison–Wesley, p. 50, ISBN 978-0-321-33570-8, https://books.google.com/books?id=56LNfE2QGtYC&q=rhythms&pg=PA50, "it was natural to consider the set of all sequences of [L] and [S] that have exactly m beats. ...there are exactly Fm+1 of them. For example the 21 sequences when m = 7 are: [gives list]. In this way Indian prosodists were led to discover the Fibonacci sequence, as we have observed in Section 1.2.8 (from v.1)"
- ↑ Sigler 2002, pp. 404–05.
- ↑ Lucas 1891, p. 3.
- ↑ Beck & Geoghegan 2010.
- ↑ Bóna 2011, p. 180.
- ↑ Knuth, Donald (1968), The Art of Computer Programming, 1, Addison Wesley, p. 100, ISBN 978-81-7758-754-8, https://books.google.com/books?id=MooMkK6ERuYC&pg=PA100, "Before Fibonacci wrote his work, the sequence Fn had already been discussed by Indian scholars, who had long been interested in rhythmic patterns... both Gopala (before 1135 AD) and Hemachandra (c. 1150) mentioned the numbers 1,2,3,5,8,13,21 explicitly [see P. Singh Historia Math 12 (1985) 229–44]" p. 100 (3d ed)..."
- ↑ 10.0 10.1 Livio 2003, p. 197.
- ↑ Agrawala, VS (1969), Pāṇinikālīna Bhāratavarṣa (Hn.). Varanasi-I: TheChowkhamba Vidyabhawan, "SadgurushiShya writes that Pingala was a younger brother of Pāṇini [Agrawala 1969, lb]. There is an alternative opinion that he was a maternal uncle of Pāṇini [Vinayasagar 1965, Preface, 121]. ... Agrawala [1969, 463–76], after a careful investigation, in which he considered the views of earlier scholars, has concluded that Pāṇini lived between 480 and 410 BC"
- ↑ Singh, Parmanand (1985), "The So-called Fibonacci Numbers in Ancient and Medieval India", Historia Mathematica (Academic Press) 12 (3): 232, doi:10.1016/0315-0860(85)90021-7
- ↑ Velankar, HD (1962), 'Vṛttajātisamuccaya' of kavi Virahanka, Jodhpur: Rajasthan Oriental Research Institute, p. 101
- ↑ Livio 2003, p. 197–198.
- ↑ Shah, Jayant (1991), "A History of Piṅgala's Combinatorics", Northeastern University: 41, https://web.northeastern.edu/shah/papers/Pingala.pdf, retrieved 4 January 2019
- ↑ Sigler 2002, pp. 404–405.
- ↑ Fibonacci's Liber Abaci (Book of Calculation), 13 December 2009, https://www.math.utah.edu/~beebe/software/java/fibonacci/liber-abaci.html, retrieved 28 November 2018
- ↑ Hemenway, Priya (2005), Divine Proportion: Phi In Art, Nature, and Science, New York: Sterling, pp. 20–21, ISBN 1-4027-3522-7
- ↑ Knott, Dr. Ron (25 September 2016), The Fibonacci Numbers and Golden section in Nature – 1, http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html#Rabbits, retrieved 27 November 2018
- ↑ Knott, Ron, Fibonacci's Rabbits, University of Surrey Faculty of Engineering and Physical Sciences, http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html#Rabbits
- ↑ Gardner, Martin (1996), Mathematical Circus, The Mathematical Association of America, p. 153, ISBN 978-0-88385-506-5, "It is ironic that Leonardo, who made valuable contributions to mathematics, is remembered today mainly because a 19th-century French number theorist, Édouard Lucas... attached the name Fibonacci to a number sequence that appears in a trivial problem in Liber abaci"
- ↑ Beutelspacher, Albrecht; Petri, Bernhard (1996), "Fibonacci-Zahlen", Der Goldene Schnitt, Vieweg+Teubner Verlag, pp. 87–98, doi:10.1007/978-3-322-85165-9_6
- ↑ Ball 2003, p. 156.
- ↑ Ball 2003, pp. 155–156.
- ↑ Sloane, N. J. A., ed. "Sequence A002390". OEIS Foundation. https://oeis.org/A002390.
- ↑ Sloane, N. J. A., ed. "Sequence A097348". OEIS Foundation. https://oeis.org/A097348.
- ↑ Kepler, Johannes (1966), A New Year Gift: On Hexagonal Snow, Oxford University Press, p. 92, ISBN 978-0-19-858120-8
- ↑ Strena seu de Nive Sexangula, 1611
- ↑ Gessel, Ira (October 1972), "Fibonacci is a Square", The Fibonacci Quarterly 10 (4): 417–19, http://www.fq.math.ca/Scanned/10-4/advanced10-4.pdf, retrieved April 11, 2012
- ↑ Dijkstra, Edsger W. (1978), In honour of Fibonacci, http://www.cs.utexas.edu/users/EWD/ewd06xx/EWD654.PDF
- ↑ Lucas 1891, p. 4.
- ↑ Vorobiev, Nikolaĭ Nikolaevich; Martin, Mircea (2002), "Chapter 1", Fibonacci Numbers, Birkhäuser, pp. 5–6, ISBN 978-3-7643-6135-8
- ↑ Flajolet, Philippe; Sedgewick, Robert (2009), Analytic Combinatorics, Cambridge University Press, p. 42, ISBN 978-0521898065
- ↑ 34.0 34.1 34.2 Weisstein, Eric W.. "Fibonacci Number". http://mathworld.wolfram.com/FibonacciNumber.html.
- ↑ Glaister, P (1995), "Fibonacci power series", The Mathematical Gazette 79 (486): 521–25, doi:10.2307/3618079
- ↑ Landau (1899) quoted according Borwein, Page 95, Exercise 3b.
- ↑ Sloane, N. J. A., ed. "Sequence A079586". OEIS Foundation. https://oeis.org/A079586.
- ↑ André-Jeannin, Richard (1989), "Irrationalité de la somme des inverses de certaines suites récurrentes", Comptes Rendus de l'Académie des Sciences, Série I 308 (19): 539–41
- ↑ Honsberger, Ross (1985), "Millin's series", Mathematical Gems III, Dolciani Mathematical Expositions, 9, American Mathematical Society, pp. 135–136, ISBN 9781470457181, https://books.google.com/books?id=vl_0DwAAQBAJ&pg=PA135
- ↑ Ribenboim, Paulo (2000), My Numbers, My Friends, Springer-Verlag
- ↑ Su, Francis E (2000), "Fibonacci GCD's, please", Mudd Math Fun Facts, et al, HMC, http://www.math.hmc.edu/funfacts/ffiles/20004.5.shtml, retrieved 2007-02-23
- ↑ Williams, H. C. (1982), "A note on the Fibonacci quotient ", Canadian Mathematical Bulletin 25 (3): 366–70, doi:10.4153/CMB-1982-053-0. Williams calls this property "well known".
- ↑ Prime Numbers, Richard Crandall, Carl Pomerance, Springer, second edition, 2005, p. 142.
- ↑ Sloane, N. J. A., ed. "Sequence A005478". OEIS Foundation. https://oeis.org/A005478.
- ↑ "Probabilizing Fibonacci numbers", Connections in Discrete Mathematics: A Celebration of the Work of Ron Graham, Cambridge University Press, 2018, pp. 1–12, ISBN 978-1-107-15398-1, https://statweb.stanford.edu/~cgates/PERSI/papers/probabilizing-fibonacci.pdf
- ↑ Honsberger, Ross (1985), "Mathematical Gems III", AMS Dolciani Mathematical Expositions (9): 133, ISBN 978-0-88385-318-4
- ↑ Cohn, J. H. E. (1964), "On square Fibonacci numbers", The Journal of the London Mathematical Society 39: 537–540, doi:10.1112/jlms/s1-39.1.537
- ↑ Pethő, Attila (2001), "Diophantine properties of linear recursive sequences II", Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 17: 81–96
- ↑ Bugeaud, Y; Mignotte, M; Siksek, S (2006), "Classical and modular approaches to exponential Diophantine equations. I. Fibonacci and Lucas perfect powers", Ann. Math. 2 (163): 969–1018, doi:10.4007/annals.2006.163.969, Bibcode: 2004math......3046B
- ↑ Luo, Ming (1989), "On triangular Fibonacci numbers", Fibonacci Quart. 27 (2): 98–108, http://www.fq.math.ca/Scanned/27-2/ming.pdf
- ↑ Luca, Florian (2000), "Perfect Fibonacci and Lucas numbers", Rendiconti del Circolo Matematico di Palermo 49 (2): 313–18, doi:10.1007/BF02904236, ISSN 1973-4409
- ↑ Broughan, Kevin A.; González, Marcos J.; Lewis, Ryan H.; Luca, Florian; Mejía Huguet, V. Janitzio; Togbé, Alain (2011), "There are no multiply-perfect Fibonacci numbers", Integers 11a: A7, http://math.colgate.edu/~integers/vol11a.html
- ↑ Luca, Florian; Mejía Huguet, V. Janitzio (2010), "On Perfect numbers which are ratios of two Fibonacci numbers", Annales Mathematicae at Informaticae 37: 107–24, ISSN 1787-6117, http://ami.ektf.hu/index.php?vol=37
- ↑ Knott, Ron, The Fibonacci numbers, UK: Surrey, http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibtable.html
- ↑ Sloane, N. J. A., ed. "Sequence A235383". OEIS Foundation. https://oeis.org/A235383.
- ↑ Ribenboim, Paulo (1996), The New Book of Prime Number Records, New York: Springer, p. 64, ISBN 978-0-387-94457-9
- ↑ Lemmermeyer 2000, pp. 73–74, ex. 2.25–28.
- ↑ Lemmermeyer 2000, pp. 73–74, ex. 2.28.
- ↑ Lemmermeyer 2000, p. 73, ex. 2.27.
- ↑ Fibonacci and Lucas factorizations, Mersennus, http://mersennus.net/fibonacci/ collects all known factors of F(i) with i < 10000.
- ↑ Factors of Fibonacci and Lucas numbers, Red golpe, http://fibonacci.redgolpe.com/ collects all known factors of F(i) with 10000 < i < 50000.
- ↑ Freyd, Peter; Brown, Kevin S. (1993), "Problems and Solutions: Solutions: E3410", The American Mathematical Monthly 99 (3): 278–79, doi:10.2307/2325076
- ↑ Sloane, N. J. A., ed. "Sequence A001175". OEIS Foundation. https://oeis.org/A001175.
- ↑ Lü, Kebo; Wang, Jun (2006), "k-step Fibonacci sequence modulo m", Utilitas Mathematica 71: 169–177, http://utilitasmathematica.com/index.php/Index/article/view/410
- ↑ Lucas 1891, p. 7.
- ↑ Stanley, Richard (2011), Enumerative Combinatorics I (2nd ed.), Cambridge Univ. Press, p. 121, Ex 1.35, ISBN 978-1-107-60262-5
- ↑ Harizanov, Valentina (1995), "Review of Yuri V. Matiyasevich, Hibert's Tenth Problem", Modern Logic 5 (3): 345–55, http://projecteuclid.org/euclid.rml/1204900767
- ↑ Pagni, David (September 2001), "Fibonacci Meets Pythagoras", Mathematics in School 30 (4): 39–40
- ↑ Stephenson, Kenneth (2005), Introduction to Circle Packing: The Theory of Discrete Analytic Functions, Cambridge University Press, ISBN 978-0-521-82356-2; see especially Lemma 8.2 (Ring Lemma), pp. 73–74, and Appendix B, The Ring Lemma, pp. 318–321.
- ↑ Knuth, Donald E (1997), The Art of Computer Programming, 1: Fundamental Algorithms (3rd ed.), Addison–Wesley, p. 343, ISBN 978-0-201-89683-1
- ↑ Adelson-Velsky, Georgy; Landis, Evgenii (1962), "An algorithm for the organization of information" (in ru), Proceedings of the USSR Academy of Sciences 146: 263–266 English translation by Myron J. Ricci in Soviet Mathematics - Doklady, 3:1259–1263, 1962.
- ↑ Avriel, M; Wilde, DJ (1966), "Optimality of the Symmetric Fibonacci Search Technique", Fibonacci Quarterly (3): 265–69
- ↑ Amiga ROM Kernel Reference Manual, Addison–Wesley, 1991
- ↑ "IFF", Multimedia Wiki, http://wiki.multimedia.cx/index.php?title=IFF#Fibonacci_Delta_Compression
- ↑ Dean Leffingwell (2021-07-01), Story, Scaled Agile Framework, https://www.scaledagileframework.com/story/, retrieved 2022-08-15
- ↑ Douady, S; Couder, Y (1996), "Phyllotaxis as a Dynamical Self Organizing Process", Journal of Theoretical Biology 178 (3): 255–74, doi:10.1006/jtbi.1996.0026, http://www.math.ntnu.no/~jarlet/Douady96.pdf
- ↑ Jones, Judy; Wilson, William (2006), "Science", An Incomplete Education, Ballantine Books, p. 544, ISBN 978-0-7394-7582-9
- ↑ Brousseau, A (1969), "Fibonacci Statistics in Conifers", Fibonacci Quarterly (7): 525–32
- ↑ "Marks for the da Vinci Code: B–", Maths (Computer Science For Fun: CS4FN), http://www.cs4fn.org/maths/bee-davinci.php
- ↑ Scott, T.C.; Marketos, P. (March 2014), On the Origin of the Fibonacci Sequence, MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Publications/fibonacci.pdf
- ↑ Livio 2003, p. 110.
- ↑ Livio 2003, pp. 112–13.
- ↑ Varenne, Franck (2010), Formaliser le vivant - Lois, Théories, Modèles, Hermann, p. 28, ISBN 9782705678128, https://www.numilog.com/LIVRES/ISBN/9782705670894.Livre?utm_source=PDF-excerpt, retrieved 2022-10-30, "En 1830, K. F. Schimper et A. Braun [...]. Ils montraient que si l'on représente cet angle de divergence par une fraction reflétant le nombre de tours par feuille ([...]), on tombe régulièrement sur un des nombres de la suite de Fibonacci pour le numérateur [...]."
- ↑ Prusinkiewicz, Przemyslaw; Hanan, James (1989), Lindenmayer Systems, Fractals, and Plants (Lecture Notes in Biomathematics), Springer-Verlag, ISBN 978-0-387-97092-9
- ↑ Vogel, Helmut (1979), "A better way to construct the sunflower head", Mathematical Biosciences 44 (3–4): 179–89, doi:10.1016/0025-5564(79)90080-4
- ↑ Livio 2003, p. 112.
- ↑ Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990), "4", The Algorithmic Beauty of Plants, Springer-Verlag, pp. 101–107, ISBN 978-0-387-97297-8, http://algorithmicbotany.org/papers/#webdocs
- ↑ "The Fibonacci sequence as it appears in nature", The Fibonacci Quarterly 1 (1): 53–56, 1963, http://www.fq.math.ca/Scanned/1-1/basin.pdf
- ↑ 89.0 89.1 Hutchison, Luke (September 2004), "Growing the Family Tree: The Power of DNA in Reconstructing Family Relationships", Proceedings of the First Symposium on Bioinformatics and Biotechnology (BIOT-04), http://fhtw.byu.edu/static/conf/2005/hutchison-growing-fhtw2005.pdf, retrieved 2016-09-03
- ↑ Livio 2003, pp. 98–99.
- ↑ "Zeckendorf representation", Encyclopedia of Math, http://www.encyclopediaofmath.org/index.php/Zeckendorf_representation
- ↑ Patranabis, D.; Dana, S. K. (December 1985), "Single-shunt fault diagnosis through terminal attenuation measurement and using Fibonacci numbers", IEEE Transactions on Instrumentation and Measurement IM-34 (4): 650–653, doi:10.1109/tim.1985.4315428, Bibcode: 1985ITIM...34..650P
- ↑ Brasch, T. von; Byström, J.; Lystad, L.P. (2012), "Optimal Control and the Fibonacci Sequence", Journal of Optimization Theory and Applications 154 (3): 857–78, doi:10.1007/s10957-012-0061-2
- ↑ Livio 2003, p. 176.
- ↑ Livio 2003, p. 193.
Works cited
- Ball, Keith M (2003), "8: Fibonacci's Rabbits Revisited", Strange Curves, Counting Rabbits, and Other Mathematical Explorations, Princeton, NJ: Princeton University Press, ISBN 978-0-691-11321-0.
- Beck, Matthias; Geoghegan, Ross (2010), The Art of Proof: Basic Training for Deeper Mathematics, New York: Springer, ISBN 978-1-4419-7022-0.
- Bóna, Miklós (2011), A Walk Through Combinatorics (3rd ed.), New Jersey: World Scientific, ISBN 978-981-4335-23-2.
- Borwein, Jonathan M. (July 1998), Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, Wiley, pp. 91–101, ISBN 978-0-471-31515-5, http://www.wiley.com/WileyCDA/WileyTitle/productCd-047131515X.html
- Lemmermeyer, Franz (2000), Reciprocity Laws: From Euler to Eisenstein, Springer Monographs in Mathematics, New York: Springer, ISBN 978-3-540-66957-9.
- Livio, Mario (2003), The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (First trade paperback ed.), New York City: Random House, ISBN 0-7679-0816-3, https://books.google.com/books?id=bUARfgWRH14C
- Lucas, Édouard (1891) (in fr), Théorie des nombres, 1, Paris: Gauthier-Villars, https://archive.org/details/thoriedesnombr01lucauoft.
- Sigler, L. E. (2002), Fibonacci's Liber Abaci: A Translation into Modern English of Leonardo Pisano's Book of Calculation, Sources and Studies in the History of Mathematics and Physical Sciences, Springer, ISBN 978-0-387-95419-6
External links
- Periods of Fibonacci Sequences Mod m at MathPages
- Scientists find clues to the formation of Fibonacci spirals in nature
- Hazewinkel, Michiel, ed. (2001), "Fibonacci numbers", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/f040020
- OEIS sequence A000045 (Fibonacci numbers)
Script error: No such module "Interwiki".