Bernoulli sampling
In the theory of finite population sampling, Bernoulli sampling is a sampling process where each element of the population is subjected to an independent Bernoulli trial which determines whether the element becomes part of the sample. An essential property of Bernoulli sampling is that all elements of the population have equal probability of being included in the sample.[1]
Bernoulli sampling is therefore a special case of Poisson sampling. In Poisson sampling each element of the population may have a different probability of being included in the sample. In Bernoulli sampling, the probability is equal for all the elements.
Because each element of the population is considered separately for the sample, the sample size is not fixed but rather follows a binomial distribution.
Example
The most basic Bernoulli method generates n random variates to extract a sample from a population of n items. Suppose you want to extract a given percentage pct of the population. The algorithm can be described as follows:[2]
for each item in the set
generate a random non-negative integer R
if (R mod 100) < pct then
select item
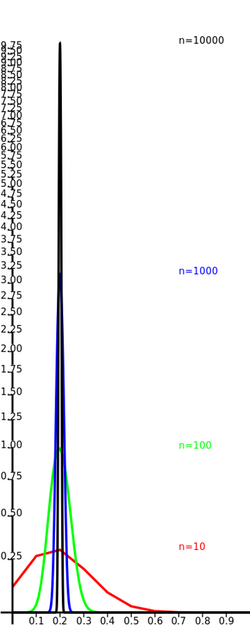
A percentage of 20%, say, is usually expressed as a probability p=0.2. In that case, random variates are generated in the unit interval. After running the algorithm, a sample of size k will have been selected. One would expect to have [math]\displaystyle{ k \approx n \cdot p }[/math], which is more and more likely as n grows. In fact, It is possible to calculate the probability of obtaining a sample size of k by the Binomial distribution:
[math]\displaystyle{ f(k,n,p) = \binom{n}{k}p^k(1-p)^{n-k} }[/math]
On the left this function is shown for four values of [math]\displaystyle{ n }[/math] and [math]\displaystyle{ p=0.2 }[/math]. In order to compare the values for different values of [math]\displaystyle{ n }[/math], the [math]\displaystyle{ k }[/math]'s in abscissa are scaled from [math]\displaystyle{ \left[0, n\right] }[/math] to the unit interval, while the value of the function, in ordinate, is multiplied by the inverse, so that the area under the graph maintains the same value —that area is related to the corresponding cumulative distribution function. The values are shown in logarithmic scale.
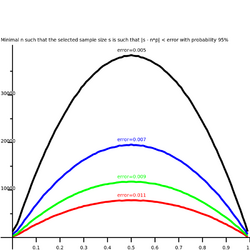
On the right the minimum values of [math]\displaystyle{ n }[/math] that satisfy given error bounds with 95% probability. Given an error, the set of [math]\displaystyle{ k }[/math]'s within bounds can be described as follows:
[math]\displaystyle{ K_{n, p} = \left\{ k \in \N: \left\vert \frac k n - p \right\vert \lt \mathrm{error} \right\} }[/math]
The probability to end up within [math]\displaystyle{ K }[/math] is given again by the binomial distribution as:
[math]\displaystyle{ \sum_{k \in K} f(k, n, p). }[/math]
The picture shows the lowest values of [math]\displaystyle{ n }[/math] such that the sum is at least 0.95. For [math]\displaystyle{ p = 0.0 }[/math] and [math]\displaystyle{ p = 1.00 }[/math] the algorithm delivers exact results for all [math]\displaystyle{ n }[/math]'s. The [math]\displaystyle{ p }[/math]'s in between are obtained by bisection. Note that, if [math]\displaystyle{ 100 \cdot p }[/math] is an integer percentage, [math]\displaystyle{ \mathrm{error} = 0.005 }[/math], guarantees that [math]\displaystyle{ 100 \cdot k/n = 100 \cdot p }[/math]. Values as high as [math]\displaystyle{ n = 38400 }[/math] can be required for such an exact match.
See also
References
- ↑ Carl-Erik Sarndal; Bengt Swensson; Jan Wretman (1992). Model Assisted Survey Sampling. ISBN 978-0-387-97528-3.
- ↑ Voratas Kachitvichyanukul; Bruce W. Schmeise (1 February 1988). "Binomial Random Variate Generation". Communications of the ACM 31 (2): 216–222. doi:10.1145/42372.42381. https://dl.acm.org/doi/10.1145/42372.42381.
External links
 |  |
