Bhargava cube
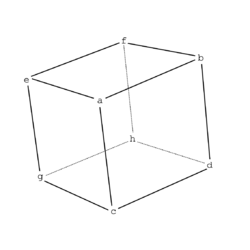
In mathematics, in number theory, a Bhargava cube (also called Bhargava's cube) is a configuration consisting of eight integers placed at the eight corners of a cube.[1] This configuration was extensively used by Manjul Bhargava, a Canadian-American Fields Medal winning mathematician, to study the composition laws of binary quadratic forms and other such forms. To each pair of opposite faces of a Bhargava cube one can associate an integer binary quadratic form thus getting three binary quadratic forms corresponding to the three pairs of opposite faces of the Bhargava cube.[2] These three quadratic forms all have the same discriminant and Manjul Bhargava proved that their composition in the sense of Gauss[3] is the identity element in the associated group of equivalence classes of primitive binary quadratic forms. (This formulation of Gauss composition was likely first due to Dedekind.)[4] Using this property as the starting point for a theory of composition of binary quadratic forms Manjul Bhargava went on to define fourteen different composition laws using a cube.
Integer binary quadratic forms
An expression of the form [math]\displaystyle{ Q(x,y)=ax^2+bxy+cy^2 }[/math], where a, b and c are fixed integers and x and y are variable integers, is called an integer binary quadratic form. The discriminant of the form is defined as
- [math]\displaystyle{ D = b^2 -4ac. }[/math]
The form is said to be primitive if the coefficients a, b, c are relatively prime. Two forms
- [math]\displaystyle{ Q(x,y) = ax^2+bxy+cy^2, \quad Q^\prime(x,y)=a^\prime x^2+b^\prime xy + c^\prime y^2 }[/math]
are said to be equivalent if there exists a transformation
- [math]\displaystyle{ x\mapsto \alpha x + \beta y,\quad y\mapsto \gamma x + \delta y }[/math]
with integer coefficients satisfying [math]\displaystyle{ \alpha\delta - \beta\gamma =1 }[/math] which transforms [math]\displaystyle{ Q(x,y) }[/math] to [math]\displaystyle{ Q^\prime(x,y) }[/math]. This relation is indeed an equivalence relation in the set of integer binary quadratic forms and it preserves discriminants and primitivity.
Gauss composition of integer binary quadratic forms
Let [math]\displaystyle{ Q(x,y) }[/math] and [math]\displaystyle{ Q^\prime(x,y) }[/math] be two primitive binary quadratic forms having the same discriminant and let the corresponding equivalence classes of forms be [math]\displaystyle{ [Q(x,y)] }[/math] and [math]\displaystyle{ [Q^\prime(x,y)] }[/math]. One can find integers [math]\displaystyle{ p,q,r,s, p^\prime, q^\prime, r^\prime, s^\prime, a^{\prime\prime}, b^{\prime\prime}, c^{\prime\prime} }[/math] such that
- [math]\displaystyle{ X=px_1x_2+qx_1y_2+ry_1x_2+sy_1y_2 }[/math]
- [math]\displaystyle{ Y=p^\prime x_1x_2 + q^\prime x_1y_2 + r^\prime y_1x_2 + s^\prime y_1y_2 }[/math]
- [math]\displaystyle{ Q^{\prime\prime}(x,y) = a^{\prime\prime}x^2 + b^{\prime\prime}xy + c^{\prime\prime}y^2 }[/math]
- [math]\displaystyle{ Q^{\prime\prime}(X,Y)=Q(x_1,y_1)Q^\prime(x_2,y_2) }[/math]
The class [math]\displaystyle{ [Q^{\prime\prime}(x,y)] }[/math] is uniquely determined by the classes [Q(x, y)] and [Q′(x, y)] and is called the composite of the classes [math]\displaystyle{ [Q(x,y)] }[/math] and [math]\displaystyle{ [Q^\prime(x,y)] }[/math].[3] This is indicated by writing
- [math]\displaystyle{ [Q^{\prime\prime}(x,y)]= [Q(x,y)]\ast [Q^\prime(x,y)] }[/math]
The set of equivalence classes of primitive binary quadratic forms having a given discriminant D is a group under the composition law described above. The identity element of the group is the class determined by the following form:
- [math]\displaystyle{ Q_{Id}^{(D)}(x,y) = \begin{cases} x^2-\frac{D}{4}y^2 & D \equiv 0 \pmod 4\\ x^2 + xy + \frac{1-D}{4}y^2 & D \equiv 1 \pmod 4 \end{cases} }[/math]
The inverse of the class [math]\displaystyle{ [a x^2 + h xy + b y^2] }[/math] is the class [math]\displaystyle{ [ a x^2 - h xy + b y^2] }[/math].
Quadratic forms associated with the Bhargava cube
Let (M, N) be the pair of 2 × 2 matrices associated with a pair of opposite sides of a Bhargava cube; the matrices are formed in such a way that their rows and columns correspond to the edges of the corresponding faces. The integer binary quadratic form associated with this pair of faces is defined as
- [math]\displaystyle{ Q=-\det (Mx+Ny) }[/math]
The quadratic form is also defined as
- [math]\displaystyle{ Q =-\det(Mx-Ny) }[/math]
However, the former definition will be assumed in the sequel.
The three forms
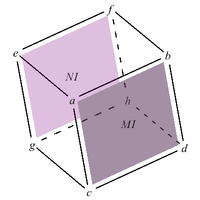
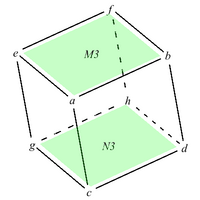
Let the cube be formed by the integers a, b, c, d, e, f, g, h. The pairs of matrices associated with opposite edges are denoted by (M1, N1), (M2, N2), and (M3, N3). The first rows of M1, M2 and M3 are respectively [a b], [a c] and [a e]. The opposite edges in the same face are the second rows. The corresponding edges in the opposite faces form the rows of the matrices N1, N2, N3 (see figure).
| right|200px|Bhargava cube showing the pair of opposite faces M2 and N2. |
The form Q1
The quadratic form associated with the faces defined by the matrices [math]\displaystyle{ M_1=\begin{bmatrix} a & b \\ c & d\end{bmatrix},N_1=\begin{bmatrix} e & f \\ g & h\end{bmatrix} }[/math] (see figure) is
- [math]\displaystyle{ Q_1=-\det(M_1x+N_1y)= -(\det(M_1)x^2 + ( ah+ed-bg-fc)xy +\det(N_1)y^2) }[/math]
The discriminant of a quadratic form Q1 is
- [math]\displaystyle{ D_1=(ah+ed-bg-fc)^2 - 4\det(M_1) \det(N_1). }[/math]
The form Q2
The quadratic form associated with the faces defined by the matrices [math]\displaystyle{ M_2=\begin{bmatrix} a & c \\ e & g\end{bmatrix},N_2=\begin{bmatrix} b & d \\ f & h\end{bmatrix} }[/math] (see figure) is
- [math]\displaystyle{ Q_2=-\det(M_2x+N_2y)= -(\det(M_2)x^2 + ( ah+bg-fc-ed)xy +\det(N_2)y^2) }[/math]
The discriminant of a quadratic form Q2 is
- [math]\displaystyle{ D_2=(ah+bg-fc-ed)^2 - 4\det(M_2) \det(N_2). }[/math]
The form Q3
The quadratic form associated with the faces defined by the matrices [math]\displaystyle{ M_3=\begin{bmatrix} a & e \\ b & f\end{bmatrix},N_3=\begin{bmatrix} c & g \\ d & h\end{bmatrix} }[/math] (see figure) is
- [math]\displaystyle{ Q_3=-\det(M_3x+N_3y)= -(\det(M_3)x^2 + ( ah+fc-ed-bg)xy +\det(N_3)y^2) }[/math]
The discriminant of a quadratic form Q3 is
- [math]\displaystyle{ D_3=(ah+fc-ed-bg)^2 - 4\det(M_3) \det(N_3). }[/math]
Relation between Q1, Q2, Q3
Manjul Bhargava's surprising discovery can be summarised thus:[2]
- If a cube A gives rise to three primitive binary quadratic forms Q1, Q2, Q3, then Q1, Q2, Q3 have the same discriminant, and the product of these three forms is the identity in the group defined by Gauss composition. Conversely, if Q1, Q2, Q3 are any three primitive binary quadratic forms of the same discriminant whose product is the identity under Gauss composition, then there exists a cube A yielding Q1, Q2, Q3.
Example
The three quadratic forms associated with the numerical Bhargava cube shown in the figure are computed as follows.
- [math]\displaystyle{ \begin{align} Q_1(x,y)=-\det(M_1x+N_1y) & = - \det\left( \begin{bmatrix} 1 & 0 \\ 0 & -2 \end{bmatrix} x + \begin{bmatrix}0 & 3 \\ 4 & 5\end{bmatrix}y\right) \\ & = -\begin{vmatrix} x & 3y \\ 4y & -2x+5y\end{vmatrix} = 2x^2-5xy+12y^2 \\ \\ Q_2(x,y)=-\det(M_2x+N_2y) & = - \det\left( \begin{bmatrix} 1 & 0 \\ 0 & 4 \end{bmatrix} x + \begin{bmatrix}0 & 3 \\ -2 & 5\end{bmatrix}y\right) \\ & = -\begin{vmatrix} x & 3y \\ -2y & 4x+5y\end{vmatrix} = -4x^2-5xy-6y^2 \\ \\ Q_3(x,y)=-\det(M_3x+N_3y) & = - \det\left( \begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix} x + \begin{bmatrix}0 & 4 \\ -2 & 5\end{bmatrix}y\right) \\ & = -\begin{vmatrix} x & 4y \\ -2y & 3x+5y\end{vmatrix} = -3x^2-5xy - 8y^2 \\ {} \end{align} }[/math]
The composition [math]\displaystyle{ [Q_1(x,y)]\ast[ Q_2(x,y)] }[/math] is the form [math]\displaystyle{ [Q(x,y)] }[/math] where [math]\displaystyle{ Q(x,y) = -3x^2+ 5xy - 8y^2 }[/math] because of the following:
- [math]\displaystyle{ X = -2x_1x_2 + 4y_1x_2 + y_1y_2 }[/math]
- [math]\displaystyle{ Y=x_1x_2+3y_1y_2 }[/math]
- [math]\displaystyle{ Q(X,Y) = Q_1(x_1,y_1)Q_2(x_2,y_2) }[/math]
Also [math]\displaystyle{ [Q_3(x,y)]^{-1}=Q(x,y) }[/math]. Thus [math]\displaystyle{ [Q_1(x,y)]\ast [Q_2(x,y)]\ast [Q_3(x,y)] }[/math] is the identity element in the group defined by the Gauss composition.
Further composition laws on forms
Composition of cubes
The fact that the composition of the three binary quadratic forms associated with the Bhargava cube is the identity element in the group of such forms has been used by Manjul Bhargava to define a composition law for the cubes themselves.[2]
Composition of cubic forms
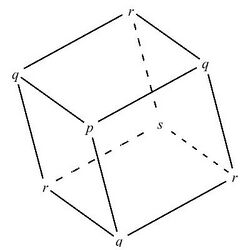
An integer binary cubic in the form [math]\displaystyle{ px^3 + 3qx^2y+3rxy^2+sy^3 }[/math] can be represented by a triply symmetric Bhargava cube as in the figure. The law of composition of cubes can be used to define a law of composition for the binary cubic forms.[2]
Composition of pairs of binary quadratic forms
The pair of binary quadratic forms [math]\displaystyle{ (ax^2+2bxy+cy^2, dx^2+2exy+fy^2) }[/math] can be represented by a doubly symmetric Bhargava cube as in the figure. The law of composition of cubes is now used to define a composition law on pairs of binary quadratic forms.[2]
See also
References
- ↑ Mak Trifkovic (2013). Algebraic Theory of Quadratic Numbers. New York: Springer. p. 175. ISBN 978-1-4614-7716-7.
- ↑ 2.0 2.1 2.2 2.3 2.4 Manjul Bhargava (2006). Higher composition laws and applications, in Proceedings of the International Congress of Mathematicians, Madrid, Spain, 2006. European Mathematical Society.
- ↑ 3.0 3.1 Carl Friedrich Gauss (translated by Arthur A Clarke) (1986). Disquisitiones Arithmeticae. Springer Verlag. pp. 230–256.
- ↑ Richard Dedekind (1932). Gesammelte Mathematische Werke. 2. Viehweg. pp. 307.
 |