Cube
A cube is a three-dimensional solid object in geometry. A cube has eight vertices and twelve straight edges of the same length, so that these edges form six square faces of the same size. It is an example of a polyhedron.
The cube is found in many popular cultures, including toys and games, the arts, optical illusions, and architectural buildings. Cubes can be found in crystal structures, science, and technological devices. It is also found in ancient texts, such as Plato's work Timaeus, which described a set of solids now called Platonic solids, associating a cube with the classical element of earth. A cube with unit length is the canonical unit of volume in three-dimensional space, relative to which other solid objects are measured.
The cube relates to the construction of many polyhedra, such as truncation and attaching to other polyhedra. It also represents geometrical shapes. The cube can be attached to its faces with its copy to fill a space without leaving a gap, which forms a honeycomb.
The cube can be represented in many ways. One example is by drawing a graph, a structure in graph theory consisting of a set of vertices that are connected with an edge. This graph also represents the family of a cuboid, a polyhedron with six quadrilateral faces, which includes the cube as its special case. The cube and its graph are a three-dimensional hypercube, a family of polytopes that also includes the two-dimensional square and four-dimensional tesseract.
Properties
File:Hexahedron.stl A cube is a polyhedron with eight vertices and twelve equal-length edges, forming six squares as its faces. A cube is a special case of a rectangular cuboid, which has six rectangular faces, each of which has a pair of opposite equal-length and parallel edges.[1] Both polyhedra have the same dihedral angle, the angle between two adjacent faces at a common edge, a right angle or 90°, obtained from the interior angle (an angle formed between two adjacent sides at a common point of a polygon within) of a square.[2][3] More generally, the cube and the rectangular cuboid are special cases of a cuboid, a polyhedron with six quadrilaterals (four-sided polygons).[4] As for all convex polyhedra, the cube has Euler characteristic of 2, according to the formula ; the three letters denote respectively the number of vertices, edges, and faces.[5]
All three square faces surrounding a vertex are orthogonal to each other, meaning the planes are perpendicular, forming a right angle between two adjacent squares. Hence, the cube is classified as an orthogonal polyhedron.[6] The cube is a special case of other cuboids. These include a parallelepiped, a polyhedron with six parallelograms faces, because its pairs of opposite faces are congruent;[7] a rhombohedron, as a special case of a parallelepiped with six rhombi faces, because the interior angle of all of the faces is right;[8] and a trigonal trapezohedron, a polyhedron with congruent quadrilateral faces, since its square faces are the special cases of rhombi.[9]
The cube is a non-composite or an elementary polyhedron. That is, no plane intersecting its surface only along edges, thereby cutting into two or more convex, regular-faced polyhedra.[10]
Measurement

Given a cube with edge length , the face diagonal of the cube is the diagonal of a square , and the space diagonal of the cube is a line connecting two vertices that are not in the same face, formulated as . Both formulas can be determined by using the Pythagorean theorem. The surface area of a cube is six times the area of a square:[11] The volume of a rectangular cuboid is the product of its length, width, and height. Because all the edges of a cube are equal in length, the formula for the volume of a cube is the third power of its side length.[11] This leads to the use of the term cube as a verb, to mean raising any number to the third power:[4]
The cube has three types of closed geodesics, or paths on a cube's surface that are locally straight. In other words, they avoid the vertices, follow line segments across the faces that they cross, and form complementary angles on the two incident faces of each edge that they cross. One type lies in a plane parallel to any face of the cube, forming a square congruent to a face, four times the length of each edge. Another type lies in a plane perpendicular to the long diagonal, forming a regular hexagon; its length is times that of an edge. The third type is a non-planar hexagon.[12]
Insphere, midsphere, circumsphere
An insphere of a cube is a sphere tangent to the faces of a cube at their centroids. Its midsphere is a sphere tangent to the edges of a cube. Its circumsphere is a sphere tangent to the vertices of a cube. With edge length , they are respectively:[13]
Unit cube

A unit cube is a cube with 1 unit in length along each edge. It follows that each face is a unit square and that the entire figure has a volume of 1 cubic unit.[14][15] Prince Rupert of the Rhine, known for Prince Rupert's drop, wagered whether a cube could be passed through a hole made in another cube of the same size. The story recounted in 1693 by English mathematician John Wallis answered that it is possible, although there were some errors in Wallis's presentation. Roughly a century later, Dutch mathematician Pieter Nieuwland provided a better solution that the edges of a cube passing through the unit cube's hole could be as large as approximately 1.06 units in length.[16][17] One way to obtain this result is by using the Pythagorean theorem or the formula for Euclidean distance in three-dimensional space.[18]
An ancient problem of doubling the cube requires the construction of a cube with a volume twice the original by using only a compass and straightedge. This was concluded by French mathematician Pierre Wantzel in 1837, proving that it is impossible to implement since a cube with twice the volume of the original—the cube root of 2, —is not constructible.[19] However, this problem was solved with folding an origami paper by (Messer 1986).[20]
Symmetry
The cube has octahedral symmetry of order 48. In other words, the cube has 48 isometries (including identity), each of which transforms the cube to itself. These transformations include nine reflection symmetries (where two halves cut by a plane are identical): three cut the cube at the midpoints of its edges, and six cut diagonally. The cube also has thirteen axes of rotational symmetry (whereby rotation around the axis results in an identical appearance): three axes pass through the centroids of opposite faces, six through the midpoints of opposite edges, and four through opposite vertices; these axes are respectively four-fold rotational symmetry (0°, 90°, 180°, and 270°), two-fold rotational symmetry (0° and 180°), and three-fold rotational symmetry (0°, 120°, and 240°).[21][22][23][24]
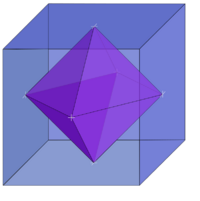
The dual polyhedron can be obtained from each of the polyhedra's vertices tangent to a plane by a process known as polar reciprocation.[25] One property of dual polyhedra is that the polyhedron and its dual share their three-dimensional symmetry point group. In this case, the dual polyhedron of a cube is the regular octahedron, and both of these polyhedra have the same octahedral symmetry.[26]
The cube is face-transitive, meaning its two square faces are alike and can be mapped by rotation and reflection.[27] It is vertex-transitive, meaning all of its vertices are equivalent and can be mapped isometrically under its symmetry.[28] It is also edge-transitive, meaning the same kind of faces surround each of its vertices in the same or reverse order, and each pair of adjacent faces has the same dihedral angle. Therefore, the cube is a regular polyhedron.[29] Each vertex is surrounded by three squares, so the cube is by vertex configuration or by Schläfli symbol.[30]
Appearances
In popular cultures
Cubes have appeared in many roles in popular culture. It is the most common form of dice.[27] Puzzle toys such as pieces of a Soma cube,[31] Rubik's Cube, and Skewb are built of cubes.[32] Minecraft is an example of a sandbox video game of cubic blocks.[33] The outdoor sculpture Alamo (1967) is a cube that spins around its vertical axis.[34] Optical illusions such as the impossible cube and Necker cube have been explored by artists such as M. C. Escher.[35] The cube was applied in Alberti's treatise on Renaissance architecture, De re aedificatoria (1450).[36] Cube houses in the Netherlands are a set of cubical houses whose hexagonal space diagonals become the main floor.[37]
In nature and science
Cubes are also found in various fields of natural science and technology. It is applied to the unit cell of a crystal known as a cubic crystal system.[38] Table salt is an example of a mineral with a commonly cubic shape.[39] Other examples are pyrite (although there are many variations)[40] and uranium cubic-shaped in nuclear program.[41] The radiolarian Lithocubus geometricus, discovered by Ernst Haeckel, has a cubic shape.[42] Cubane is a synthetic hydrocarbon consisting of eight carbon atoms arranged at the corners of a cube, with one hydrogen atom attached to each carbon atom.[43]
A historical attempt to unify three physics ideas of relativity, gravitation, and quantum mechanics used the framework of a cube known as a cGh cube.[44]
Technological cubes include the spacecraft device CubeSat,[45] thermal radiation demonstration device Leslie cube,[46] and web server machine Cobalt Qube.[47] Cubical grids are usual in three-dimensional Cartesian coordinate systems.[48] In computer graphics, an algorithm divides the input volume into a discrete set of cubes known as the unit on isosurface,[49] and the faces of a cube can be used for mapping a shape.[50] In various areas of engineering, including traffic signs and radar, the corner of a cube is useful as a retroreflector, called a corner reflector, which redirects any ray or wave back to its source.[51]
In antiquity
The Platonic solids are five polyhedra known since antiquity. The set is named for Plato, who attributed these solids to nature in his dialogue Timaeus. One of them, the cube, represented the classical element of earth because of the building blocks of Earth's foundation.[52] Euclid's Elements defined the Platonic solids, including the cube, and showed how to find the ratio of the circumscribed sphere's diameter to the edge length.[53]
Following Plato's use of the regular polyhedra as symbols of nature, Johannes Kepler in his Harmonices Mundi sketched each of the Platonic solids; he decorated the cube's side with a tree.[54] In his Mysterium Cosmographicum, Kepler proposed the structure of Solar System and the relationships between its extraterrestrial planets with the set of Platonic solids, inscribed and circumscribed by spherical orbs. Each solid encased in a sphere, within one another, would produce six layers, corresponding to the six known planets. Mercury, Venus, Earth, Mars, Jupiter, and Saturn. From innermost to outermost, these solids were arranged from octahedron, followed by the icosahedron, dodecahedron, tetrahedron, and eventually the cube.[55]
Constructions

The cube has eleven different nets, which consist of an arrangement of edge-joined squares. These squares can be folded along the edges and connected to those polygons, which eventually become the faces of a cube.[56][57]
One can construct a cube by attaching the six square pyramids and their apices are at the center.[58]
In analytic geometry, a cube can be constructed using the Cartesian coordinate systems. For a cube centered at the origin, with edges parallel to the axes and with an edge length of 2, the Cartesian coordinates of the vertices are .[59] Its interior consists of all points with for all . A cube's surface with center and edge length of is the locus of all points such that
The cube is a Hanner polytope, because it can be constructed by using the Cartesian product of three line segments. Its dual polyhedron, the regular octahedron, is constructed by the direct sum of three line segments.[60]
Representation
As a graph
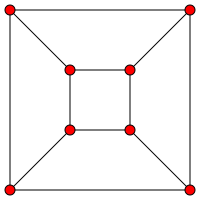
The cube can be drawn into a graph, a structure in graph theory consisting of a set of vertices that are connected with an edge. It is attainable according to Steinitz's theorem, which states that a graph can be represented as the vertex-edge graph of a polyhedron, as long as it possesses the following two properties. These are planarity (the edges of a graph are connected to every vertex without crossing other edges), and 3-connected (whenever a graph with more than three vertices, and two of the vertices are removed, the edges remain connected).[61][62] The skeleton of a cube, represented as the graph, is called the cubical graph, a Platonic graph. It has the same number of vertices and edges as the cube, twelve vertices and eight edges.[63] The cubical graph is also classified as a prism graph, resembling the skeleton of a cuboid.[64]
The cubical graph is a special case of hypercube graph or -cube—denoted as —because it can be constructed by using the Cartesian product of graphs: two graphs connecting the pair of vertices with an edge to form a new graph.[65] In the case of the cubical graph, it is the product of , where denotes the Cartesian product of graphs. In other words, the cubical graph is constructed by connecting each vertex of two squares with an edge. Notationally, the cubical graph is .[66] Like any hypercube graph, it has a cycle which visits every vertex exactly once,[67] and it is also an example of a unit distance graph.[68]
The cubical graph is bipartite, meaning every independent set of four vertices can be disjoint and the edges connected in those sets.[69] However, every vertex in one set cannot connect all vertices in the second, so this bipartite graph is not complete.[70] It is an example of both a crown graph and a bipartite Kneser graph.[71][69]
In orthogonal projection
An object illuminated by parallel rays of light casts a shadow on a plane perpendicular to those rays, called an orthogonal projection. A polyhedron is considered equiprojective if, for some position of the light, its orthogonal projection is a regular polygon. The cube is equiprojective because, if the light is parallel to one of the four lines joining a vertex to the opposite vertex, its projection is a regular hexagon.[72]
As a configuration matrix
The cube can be represented as a configuration matrix, a matrix in which the rows and columns correspond to the elements of a polyhedron as the vertices, edges, and faces. The diagonal of a matrix denotes the number of each element that appears in a polyhedron, whereas the non-diagonal of a matrix denotes the number of the column's elements that occur in or at the row's element. The cube's eight vertices, twelve edges, and six faces are denoted by each element in a matrix's diagonal (8, 12, and 6). The first column of the middle row indicates that there are two vertices on each edge, denoted as 2; the middle column of the first row indicates that three edges meet at each vertex, denoted as 3. The configuration matrix of a cube is:[73]
Related topics
Construction of polyhedra
Many polyhedra can be constructed based on a cube. Examples include:
- When faceting a cube, meaning removing part of the polygonal faces without creating new vertices of a cube, the resulting polyhedron is the stellated octahedron.[74]
- New convex polyhedra can be constructed by attaching less-regular polyhedra to a cube's faces.[10] The cube is thus a component of two Johnson solids, the elongated square pyramid and elongated square bipyramid, the latter being a cube with square pyramids on opposite faces.[75]
- Attaching a low pyramid to each face of a cube produces its Kleetope, the tetrakis hexahedron,[76] dual to the truncated octahedron.
- The barycentric subdivision of a cube (or its dual, the regular octahedron) is the disdyakis dodecahedron, a Catalan solid.[77]
- The corner region of a cube can also be truncated by a plane (e.g., spanned by the three neighboring vertices), resulting in a trirectangular tetrahedron.[78]
- The snub cube is an Archimedean solid that can be constructed by separating the cube's faces, and filling the gaps with twisted angle equilateral triangles, a process known as a snub.[79]
- Each of the cube's vertices can be truncated, and the resulting polyhedron is the Archimedean solid, the truncated cube.[80] When its edges are truncated, it is a rhombicuboctahedron.[81] Relatedly, the rhombicuboctahedron can also be constructed by separating the cube's faces and then spreading away, after which adding other triangular and square faces between them; this is known as the "expanded cube". The same figure can be derived in the same way from the cube's dual, the regular octahedron.[82]
- The chamfered cube is constructed from a cube by a truncating operator called chamfer. The resulting polyhedron has twelve hexagonal and six square centrally symmetric faces, a zonohedron.[83][84]
- Three mutually perpendicular golden rectangles can be constructed from a pair of vertices located on the midpoints of the opposite edges on a cube's surface, drawing a segment line between those two, and dividing that segment line in a golden ratio from its midpoint. The corners of these rectangles are the vertices of a regular icosahedron with twenty equilateral triangles.[85]
Polycubes
A polycube is a solid figure formed by joining one or more equal cubes face-to-face. Polycubes are the three-dimensional analogues of two-dimensional polyominoes.[86]
When four cubes are stacked vertically, and four others are attached to the second-from-top cube of the stack, the resulting polycube is the Dalí cross, named after Spanish surrealist artist Salvador Dalí, whose painting Corpus Hypercubus (1954) contains a tesseract unfolding into a six-armed cross; a similar construction is central to Robert A. Heinlein's short story "And He Built a Crooked House" (1940).[87][88] The Dalí cross can be folded in a fourth dimension to enclose a tesseract.[89] A cube is a three-dimensional instance of a hypercube (also known as a 3-cube); the two-dimensional hypercube (2-cube) is a square, and the four-dimensional hypercube (4-cube) is a tesseract.[90]
Space-filling

A cube can achieve a honeycomb by filling together with its copy in three-dimensional space without leaving a gap. Cubes are space-fillings, where the phrase "space-filling" can be understood as a generalized tessellation.[91] The cube is a plesiohedron, a special kind of space-filling polyhedron that can be defined as the Voronoi cell of a symmetric Delone set.[92] The plesiohedra include the parallelohedra, which can be translated without rotating to fill a space in which each face of any of its copies is attached to a like face of another copy. There are five kinds of parallelohedra, one of which is the parallelepiped.[93] Every three-dimensional parallelohedron is a zonohedron, a centrally symmetric polyhedron whose faces are centrally symmetric polygons.[94]
An example of a honeycomb with a cubic type only, called a cell, is a cubic honeycomb that consists of four cubes around its edges in Euclidean three-dimensional space.[95][96] More examples in three-dimensional non-Euclidean space are the honeycomb with three cubes around its edges in a three-dimensional sphere and the honeycomb with five cubes around its edges in hyperbolic space.[96]
Any parallelepiped, including a cube, can achieve a honeycomb if its Dehn invariant is zero.[97] The Dehn invariant's inception dates back to Hilbert's third problem, whether every two equal-volume polyhedra can always be dissected into polyhedral pieces and reassembled into each other. If yes, then the volume of any polyhedron could be defined axiomatically as the volume of an equivalent cube into which it could be reassembled. This problem was solved by Max Dehn, inventing his invariant, answering that not all polyhedra can be reassembled into a cube.[98] It showed that two equal volume polyhedra should have the same Dehn invariant, except for the two tetrahedra whose Dehn invariants were different.[99]
Miscellanea
The polyhedral compounds, in which the cubes share the same centre, are uniform polyhedron compounds, meaning they are polyhedral compounds whose constituents are identical—although possibly enantiomorphous—uniform polyhedra, in an arrangement that is also uniform. Respectively, the list of compounds enumerated by (Skilling 1976) in the seventh to ninth uniform compounds for the compound of six cubes with rotational freedom, three cubes, and five cubes.[100] Two compounds, consisting of two and three cubes were found in Escher's wood engraving print Stars and Max Brückner's book Vielecke und Vielflache.[101]
The spherical cube represents the spherical polyhedron, which can be modeled with the arcs of great circles, creating bounds as the edges of a spherical square.[102] Hence, the spherical cube consists of six spherical squares with 120° interior angles on each vertex. It has vector equilibrium, meaning that the distance from the centroid and each vertex is the same as the distance from that to each edge.[103][104] Its dual is the spherical octahedron.[102]
The topological object three-dimensional torus is a topological space defined to be homeomorphic to the Cartesian product of three circles. It can be represented as a three-dimensional model of the cube shape.[105]
A cube can have fractal shapes, which retain the pattern shape recursively regardless of the magnification. The Menger sponge is an example of a fractal-shaped cube, analogous to the two-dimensional version, the Sierpiński carpet.[106] Other varieties are the Jerusalem cube and Mosely snowflake.[107][108]
See also
- Bhargava cube, a configuration to study the law of binary quadratic form and other such forms, of which the cube's vertices represent the integer.
- Chazelle polyhedron, a notched opposite faces of a cube.
- Cubism, an art movement of revolutionized painting and the visual arts.
- Hemicube, an abstract polyhedron produced by identifying opposite faces of a cube
- Kaaba, cubic buildings of importance to Islam.
- Magic cube, a magic square in three-dimensional version
- Schläfli double six, a configuration of 30 points and 12 lines in three-dimensional Euclidean space
- Squaring the square's three-dimensional analogue, cubing the cube
- Superellipsoid, a solid whose horizontal sections are of the same squareness
- Tychonoff cube, generalization of a unit cube
References
- ↑ Dupuis, Nathan Fellowes (1893). Elements of Synthetic Solid Geometry. Macmillan. p. 68. https://archive.org/details/elementssynthet01dupugoog/page/n68.
- ↑ "Convex Polyhedra with Regular Faces". Canadian Journal of Mathematics 18: 169–200. 1966. doi:10.4153/cjm-1966-021-8. See table II, line 3.
- ↑ Bird, John (2020). Science and Mathematics for Engineering (6th ed.). Routledge. pp. 143–144. ISBN 9780429261701. https://books.google.com/books?id=GVbGDwAAQBAJ&pg=PA143.
- ↑ 4.0 4.1 Mills, Steve; Kolf, Hillary (1999). Maths Dictionary. Heinemann. p. 16. ISBN 9780435024741. https://books.google.com/books?id=dvFfTAR6XwEC&pg=PA16.
- ↑ Euler's Gem: The Polyhedron Formula and the Birth of Topology. Princeton University Press. 2008. pp. 1–2. ISBN 9780691126777.
- ↑ "Orthogonal Icosahedra". Nordisk Matematisk Tidskrift 15 (2): 90–96. 1967.
- ↑ Calter, Paul; Calter, Michael (2011). Technical Mathematics. John Wiley & Sons. p. 197. ISBN 9780470534922. https://books.google.com/books?id=4fHwTZK3JEIC&pg=PA197.
- ↑ Hoffmann (2020), p. 83.
- ↑ Chilton, B. L. (1963). "Polar Zonohedra". The American Mathematical Monthly 70 (9): 946–951. doi:10.1080/00029890.1963.11992147.
- ↑ 10.0 10.1 Timofeenko, A. V. (2010). "Junction of Non-composite Polyhedra". St. Petersburg Mathematical Journal 21 (3): 483–512. doi:10.1090/S1061-0022-10-01105-2. https://www.ams.org/journals/spmj/2010-21-03/S1061-0022-10-01105-2/S1061-0022-10-01105-2.pdf.
- ↑ 11.0 11.1 Khattar, Dinesh (2008). Guide to Objective Arithmetic (2nd ed.). Pearson Education. p. 377. ISBN 9788131716823. https://books.google.com/books?id=BoBCOYuOlzkC&pg=PA377.
- ↑ Fuchs, Dmitry; Fuchs, Ekaterina (2007). "Closed Geodesics on Regular Polyhedra". Moscow Mathematical Journal 7 (2): 265–279. https://web.archive.org/web/20180304110822id_/http://www.ams.org:80/distribution/mmj/vol7-2-2007/fuchs.pdf. See Figure 11, p. 273, for showing three types of cube's geodesics.
- ↑ (Coxeter 1973) Table I(i), pp. 292–293. See the columns labeled , , and , Coxeter's notation for the circumradius, midradius, and inradius, respectively, also noting that Coxeter uses as the edge length (see p. 2).
- ↑ Ball, Keith (2010). "High-dimensional Geometry and Its Probabilistic Analogues". The Princeton Companion to Mathematics. Princeton University Press. p. 671. ISBN 9781400830398.
- ↑ Geometry: Reteaching Masters. Holt Rinehart & Winston. 2001. p. 74. ISBN 9780030543289.
- ↑ Jerrard, Richard P.; Wetzel, John E. (2004). "Prince Rupert's rectangles". The American Mathematical Monthly 111 (1): 22–31. doi:10.2307/4145012.
- ↑ Rickey, V. Frederick (2005). "Dürer's Magic Square, Cardano's Rings, Prince Rupert's Cube, and Other Neat Things". http://www.math.usma.edu/people/Rickey/papers/ShortCourseAlbuquerque.pdf. Notes for “Recreational Mathematics: A Short Course in Honor of the 300th Birthday of Benjamin Franklin,” Mathematical Association of America, Albuquerque, NM, August 2–3, 2005
- ↑ The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems: Number Theory, Algebra, Geometry, Probability, Topology, Game Theory, Infinity, and Other Topics of Recreational Mathematics. W. W. Norton & Company. 2001. pp. 172–173. ISBN 9780393020236. https://books.google.com/books?id=orz0SDEakpYC&pg=PA172.
- ↑ Lützen, Jesper (2010). "The Algebra of Geometric Impossibility: Descartes and Montucla on the Impossibility of the Duplication of the Cube and the Trisection of the Angle" (in en). Centaurus 52 (1): 4–37. doi:10.1111/j.1600-0498.2009.00160.x. https://onlinelibrary.wiley.com/doi/10.1111/j.1600-0498.2009.00160.x.
- ↑ Messer, Peter (1986). "Problem 1054". Crux Mathematicorum 12 (10): 284–285. https://cms.math.ca/crux/backfile/Crux_v12n10_Dec.pdf.
- ↑ French, Doug (1988). "Reflections on a Cube". Mathematics in School 17 (4): 30–33.
- ↑ Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. p. 309. ISBN 9780521554329. https://archive.org/details/polyhedra0000crom/page/309.
- ↑ Cunningham, Gabe; Pellicer, Daniel (2024). "Finite 3-orbit Polyhedra in Ordinary Space, II". Boletín de la Sociedad Matemática Mexicana 30 (32). doi:10.1007/s40590-024-00600-z. See p. 276.
- ↑ Kane, Richard (2001). Reflection Groups and Invariant Theory. Springer. p. 16. ISBN 9780387989792. https://books.google.com/books?id=KmL1uuiMyFUC&pg=PA16.
- ↑ "3.2 Duality". Mathematical Models (2nd ed.). Clarendon Press. 1961. pp. 78–79.
- ↑ Erickson, Martin (2011). Beautiful Mathematics. Mathematical Association of America. p. 62. ISBN 9781614445098. https://books.google.com/books?id=LgeP62-ZxikC&pg=PA62.
- ↑ 27.0 27.1 McLean, K. Robin (1990). "Dungeons, Dragons, and Dice". The Mathematical Gazette 74 (469): 243–256. doi:10.2307/3619822. See p. 247.
- ↑ "Isogonal Prismatoids". Discrete & Computational Geometry 18 (1): 13–52. 1997. doi:10.1007/PL00009307.
- ↑ Senechal, Marjorie (1989). "A Brief Introduction to Tilings". in Jarić, Marko. Introduction to the Mathematics of Quasicrystals. Academic Press. p. 12. https://books.google.com/books?id=OToVjZW9CKMC&pg=PA12.
- ↑ Walter, Steurer; Deloudi, Sofia (2009). Crystallography of Quasicrystals: Concepts, Methods and Structures. Springer Series in Materials Science. 126. p. 50. doi:10.1007/978-3-642-01899-2. ISBN 9783642018985. https://books.google.com/books?id=nVx-tu596twC&pg=PA50.
- ↑ Masalski, William J. (1977). "Polycubes". The Mathematics Teacher 70 (1): 46–50. doi:10.5951/MT.70.1.0046.
- ↑ Joyner, David (2008). Adventures in Group Theory: Rubik's Cube, Merlin's Machine, and Other Mathematical Toys (2nd ed.). The Johns Hopkins University Press. p. 76. ISBN 9780801890123. https://books.google.com/books?id=6an_DwAAQBAJ&pg=PA76.
- ↑ Moore, Kimberly (2018). "Minecraft Comes to Math Class". Mathematics Teaching in the Middle School 23 (6): 334–341. doi:10.5951/mathteacmiddscho.23.6.0334.
- ↑ Reaven, Marci; Zeilten, Steve (2006). Hidden New York: A Guide to Places that Matter. Rutgers University Press. p. 77. ISBN 9780813538907. https://books.google.com/books?id=xgOtV4Nynd0C&pg=PA77.
- ↑ Impossibility: The Limits of Science and the Science of Limits. Oxford University Press. 1999. p. 14. ISBN 9780195130829. https://books.google.com/books?id=0jRa1a4pD5IC&pg=PA14.
- ↑ March, Lionel (1996). "Renaissance Mathematics and Architectural Proportion in Alberti's De re aedificatoria". Architectural Research Quarterly 2 (1): 54–65. doi:10.1017/S135913550000110X.
- ↑ Alsina, Claudi; Nelsen, Roger B. (2015). A Mathematical Space Odyssey: Solid Geometry in the 21st Century. 50. Mathematical Association of America. p. 85. ISBN 9781614442165. https://books.google.com/books?id=FEl2CgAAQBAJ&pg=PA85.
- ↑ Tisza, Miklós (2001). Physical Metallurgy for Engineers. ASM International. p. 45. ISBN 9781615032419. https://books.google.com/books?id=y1eTDQRdI2wC&pg=PA45.
- ↑ Chieh, Chung (2013). "Polyhedra and Crystal Structures". in Senechal, Marjorie. Shaping Space: Exploring Polyhedra in Nature, Art, and the Geometrical Imagination. Springer. p. 141. doi:10.1007/978-0-387-92714-5_10. ISBN 9780387927138. https://books.google.com/books?id=kZtCAAAAQBAJ&pg=PA141.
- ↑ Hoffmann, Frank (2020). Introduction to Crystallography. Springer. p. 35. doi:10.1007/978-3-030-35110-6. ISBN 9783030351106. https://books.google.com/books?id=16H0DwAAQBAJ&pg=PA35.
- ↑ Kratz, Jens-Volker (2021). Nuclear and Radiochemistry: Fundamentals and Applications. John Wiley & Sons. p. 31. doi:10.1002/9783527831944. ISBN 9783527831944. https://books.google.com/books?id=fsZAEAAAQBAJ&pg=PA31.
- ↑ (in de) Kunstformen der Natur. 1904. See here for an online book.
- ↑ Biegasiewicz, Kyle; Griffiths, Justin; Savage, G. Paul; Tsanakstidis, John; Priefer, Ronny (2015). "Cubane: 50 Years Later". Chemical Reviews 115 (14): 6719–6745. doi:10.1021/cr500523x. PMID 26102302.
- ↑ Padmanabhan, Thanu (2015). "The Grand Cube of Theoretical Physics". Sleeping Beauties in Theoretical Physics. Springer. pp. 1–8. ISBN 9783319134420.
- ↑ Helvajian, Henry; Janson, Siegfried W., eds (2008). Small Satellites: Past, Present, and Future. Aerospace Press. p. 159. ISBN 9781884989223.
- ↑ Vollmer, Michael; Möllmann, Klaus-Peter (2011). Infrared Thermal Imaging: Fundamentals, Research and Applications. John Wiley & Sons. pp. 36–38. ISBN 9783527641550. https://books.google.com/books?id=b-MqbyPwAuoC&pg=PA36.
- ↑ Sims, Ralph (Oct 1, 1998). "Cobalt Qube Microserver". Linux Journal. http://www.linuxjournal.com/article/3052.
- ↑ Kov´acs, Gergely; Nagy, Benedek Nagy; Stomfai, Gergely; Turgay, Nes¸et Deni̇z; Vizv´ari, B´ela (2021). "On Chamfer Distances on the Square and Body-Centered CubicGrids: An Operational Research Approach". Mathematical Problems in Engineering: 1–9. doi:10.1155/2021/5582034.
- ↑ Chin, Daniel Jie Yuan Chin; Mohamed, Ahmad Sufril Azlan; Shariff, Khairul Anuar; Ishikawa, Kunio (23–25 November 2021). "Advances in Visual Informatics". 7th International Visual Informatics Conference. Kajang, Malaysia. p. 376.
- ↑ Greene, N (1986). "Environment Mapping and Other Applications of World Projections". IEEE Computer Graphics and Applications 6 (11): 21–29. doi:10.1109/MCG.1986.276658. Bibcode: 1986ICGA....6k..21G.
- ↑ Kraus, John D.; Fleisch, Daniel A. (1999). Electromagnetics With Applications. Boston: McGraw Hill. pp. 324. ISBN 0-07-289969-7. http://archive.org/details/electromagnetics0000krau.
- ↑ Domokos, Gábor; Jerolmack, Douglas J.; Kun, Ferenc; Török, János (2020). "Plato's Cube and the Natural Geometry of Fragmentation". Proceedings of the National Academy of Sciences of the United States of America 117 (31): 18178–18185. doi:10.1073/pnas.2001037117. PMID 32680966. Bibcode: 2020PNAS..11718178D.
- ↑ The Thirteen Books of Euclid's Elements (3rd ed.). Cambridge University Press. 1908. pp. 262, 478, 480. https://archive.org/details/thirteenbookseu03heibgoog/page/480.
- ↑ Cromwell (1997), p. 55.
- ↑ The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (1st trade paperback ed.). Broadway Books. 2003. p. 147. ISBN 9780767908160. https://books.google.com/books?id=bUARfgWRH14C.
- ↑ Jeon, Kyungsoon (2009). "Mathematics Hiding in the Nets for a CUBE". Teaching Children Mathematics 15 (7): 394–399. doi:10.5951/TCM.15.7.0394.
- ↑ Turney, Peter D. (1984–1985). "Unfolding the Tesseract". Journal of Recreational Mathematics 17 (1). https://unfolding.apperceptual.com/.
- ↑ Barnes, John (2012). Gems of Geometry (2nd ed.). Springer. p. 82. doi:10.1007/978-3-642-30964-9. ISBN 9783642309649. https://books.google.com/books?id=7YCUBUd-4BQC&pg=PA82.
- ↑ Smith, James (2000). Methods of Geometry. John Wiley & Sons. p. 392. ISBN 9781118031032. https://books.google.com/books?id=B0khWEZmOlwC&pg=PA392.
- ↑ Kozachok, Marina (2012). "Yaroslavl International Conference "Discrete Geometry" Dedicated to the Centenary of A.D. Alexandrov (Yaroslavl, August 13-18, 2012)". P.G. Demidov Yaroslavl State University, International B.N. Delaunay Laboratory. pp. 46–49. https://www.dcglab.uniyar.ac.ru/sites/default/files/papers/Alexandrov2012Thesis.pdf#page=46.
- ↑ "13.1 Steinitz's Theorem". Convex Polytopes. Graduate Texts in Mathematics. 221 (2nd ed.). Springer-Verlag. 2003. pp. 235–244. ISBN 0387404090.
- ↑ "Chapter 4: Steinitz' Theorem for 3-Polytopes". Lectures on Polytopes. Graduate Texts in Mathematics. 152. Springer-Verlag. 1995. pp. 103–126. ISBN 038794365X.
- ↑ Rudolph, Michael (2022). The Mathematics of Finite Networks: An Introduction to Operator Graph Theory. Cambridge University Press. p. 25. doi:10.1017/9781316466919. ISBN 9781316466919. https://books.google.com/books?id=NIdoEAAAQBAJ&pg=PA25.
- ↑ Pisanski, Tomaž; Servatius, Brigitte (2013). Configuration from a Graphical Viewpoint. Springer. p. 21. doi:10.1007/978-0-8176-8364-1. ISBN 9780817683634. https://books.google.com/books?id=3vnEcMCx0HkC&pg=PA21.
- ↑ "A Survey of the Theory of Hypercube Graphs". Computers & Mathematics with Applications 15 (4): 277–289. 1988. doi:10.1016/0898-1221(88)90213-1.
- ↑ Chartrand, Gary; Zhang, Ping (2012). A First Course in Graph Theory. Dover Publications. p. 25. ISBN 9780486297309. https://books.google.com/books?id=zA_CAgAAQBAJ&pg=PA25.
- ↑ Gross, Jonathan L.; Yellen, Yellen (2006). Graph Theory and Its Applications, Second Edition. Taylor & Francis. p. 273. ISBN 9781584885054. https://books.google.com/books?id=-7Q_POGh-2cC&pg=PA273.
- ↑ Horvat, Boris (2010). "Products of Unit Distance Graphs". Discrete Mathematics 310 (12): 1783–1792. doi:10.1016/j.disc.2009.11.035.
- ↑ 69.0 69.1 Berman, Leah (2014). "Geometric Constructions for Symmetric 6-Configurations". Rigidity and Symmetry. Fields Institute Communications. 70. Springer. p. 84. doi:10.1007/978-1-4939-0781-6. ISBN 9781493907816. https://books.google.com/books?id=_n4eBAAAQBAJ&pg=PA84.
- ↑ Aldous, Joan; Wilson, Robin (2000). Graphs and Applications: An Introductory Approach. Springer. ISBN 9781852332594. https://books.google.com/books?id=1qRvTI_oWUAC&pg=PA382.
- ↑ Kitaev, Sergey; Lozin, Vadim (2015). Words and Graphs. p. 171. doi:10.1007/978-3-319-25859-1. ISBN 9783319258591. https://books.google.com/books?id=EXH_CgAAQBAJ&pg=PA171.
- ↑ Hasan, Masud; Hossain, Mohammad M.; López-Ortiz, Alejandro; Nusrat, Sabrina; Quader, Saad A.; Rahman, Nabila (2010). "Some New Equiprojective Polyhedra". arXiv:1009.2252 [cs.CG].
- ↑ Regular Polytopes (3rd ed.). New York: Dover Publications. 1973. pp. 122–123. See §1.8 Configurations.
- ↑ Inchbald, Guy (2006). "Facetting Diagrams". The Mathematical Gazette 90 (518): 253–261. doi:10.1017/S0025557200179653.
- ↑ Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. p. 84–89. doi:10.1007/978-93-86279-06-4. ISBN 9789386279064. https://books.google.com/books?id=afJdDwAAQBAJ&pg=PA84.
- ↑ Slobodan, Mišić; Obradović, Marija; Ðukanović, Gordana (2015). "Composite Concave Cupolae as Geometric and Architectural Forms". Journal for Geometry and Graphics 19 (1): 79–91. https://www.heldermann-verlag.de/jgg/jgg19/j19h1misi.pdf.
- ↑ Langer, Joel C.; Singer, David A. (2010). "Reflections on the Lemniscate of Bernoulli: The Forty-Eight Faces of a Mathematical Gem". Milan Journal of Mathematics 78 (2): 643–682. doi:10.1007/s00032-010-0124-5.
- ↑ Coxeter (1973), p. 71.
- ↑ Holme, A. (2010). Geometry: Our Cultural Heritage. Springer. doi:10.1007/978-3-642-14441-7. ISBN 9783642144417. https://books.google.com/books?id=zXwQGo8jyHUC.
- ↑ Cromwell (1997), pp. 81–82.
- ↑ Linti, G. (2013). "Catenated Compounds - Group 13 [Al, Ga, In, Tl"]. Comprehensive Inorganic Chemistry II: From Elements to Applications. Newnes. p. 41. ISBN 9780080965291. https://books.google.com/books?id=_4C7oid1kQQC&pg=RA7-PA41.
- ↑ Viana, Vera; Xavier, João Pedro; Aires, Ana Paula; Campos, Helena (2019). "Interactive Expansion of Achiral Polyhedra". in Cocchiarella, Luigi. ICGG 2018 - Proceedings of the 18th International Conference on Geometry and Graphics 40th Anniversary - Milan, Italy, August 3-7, 2018. Advances in Intelligent Systems and Computing. 809. Springer. p. 1123. doi:10.1007/978-3-319-95588-9. ISBN 9783319955872. See Fig. 6.
- ↑ Gelişgen, Özcan; Yavuz, Serhat (2019). "Isometry Groups of Chamfered Cube and Chamfered Octahedron Spaces". Mathematical Sciences and Applications E-Notes 7 (2): 174–182. doi:10.36753/mathenot.542272. https://dergipark.org.tr/en/pub/mathenot/issue/49271/542272.
- ↑ Deza, Antoinea; Michel, Deza; Grishukhin, Viatcheslav (1998). "Fullerenes and Coordination Polyhedra versus Half-cube Embeddings". Discrete Mathematics 192 (1–3): 41–80. doi:10.1016/S0012-365X(98)00065-X.
- ↑ Cromwell (1997), p. 70.
- ↑ Lunnon, W. F. (1972). "Symmetry of Cubical and General Polyominoes". in Read, Ronald C.. Graph Theory and Computing. New York: Academic Press. pp. 101–108. ISBN 9781483255125. https://books.google.com/books?id=ja7iBQAAQBAJ&pg=PA101.
- ↑ Kemp, Martin (1 January 1998). "Dali's Dimensions". Nature 391 (27): 27. doi:10.1038/34063. Bibcode: 1998Natur.391...27K.
- ↑ Fowler, David (2010). "Mathematics in Science Fiction: Mathematics as Science Fiction". World Literature Today 84 (3): 48–52. doi:10.1353/wlt.2010.0188. "Robert Heinlein's "And He Built a Crooked House," published in 1940, and Martin Gardner's "The No-Sided Professor," published in 1946, are among the first in science fiction to introduce readers to the Moebius band, the Klein bottle, and the hypercube (tesseract).".
- ↑ "19th Japan Conference on Discrete and Computational Geometry, Graphs, and Games (JCDCG^3 2016)". 2016.
- ↑ "The Projection of Fourfold Figures on a Three-flat". American Journal of Mathematics 15 (2): 179–189. 1893. doi:10.2307/2369565.
- ↑ "Polytopes that Fill and Scissors Congruence". Discrete & Computational Geometry 13 (3–4): 573–583. 1995. doi:10.1007/BF02574064.
- ↑ Erdahl, R. M. (1999). "Zonotopes, Dicings, and Voronoi's Conjecture on Parallelohedra". European Journal of Combinatorics 20 (6): 527–549. doi:10.1006/eujc.1999.0294.. Voronoi conjectured that all tilings of higher-dimensional spaces by translates of a single convex polytope are combinatorially equivalent to Voronoi tilings, and Erdahl proves this in the special case of zonotopes. But as he writes (p. 429), Voronoi's conjecture for dimensions at most four was already proven by Delaunay. For the classification of three-dimensional parallelohedra into these five types, see "Tilings with congruent tiles". Bulletin of the American Mathematical Society. New Series 3 (3): 951–973. 1980. doi:10.1090/S0273-0979-1980-14827-2.
- ↑ Horváth, Ákos G. (1995). "On Dirichlet–Voronoi Cell, Part I: Classical Problems". Periodica Polytechnica Mechanical Engineering 39 (1): 25–42. https://pp.bme.hu/me/article/view/5495.
- ↑ In higher dimensions, however, there exist parallelopes that are not zonotopes. See e.g. Shephard, G. C. (1974). "Space-filling Zonotopes". Mathematika 21 (2): 261–269. doi:10.1112/S0025579300008652.
- ↑ The Beauty of Geometry: Twelve Essays. Dover Publications. 1968. p. 167. ISBN 9780486409191. https://books.google.com/books?id=p4o-Uf-i-IUC&pg=PA212. See table III.
- ↑ 96.0 96.1 Nelson, Roice; Segerman, Henry (2017). "Visualizing Hyperbolic Honeycombs". Journal of Mathematics and the Arts 11 (1): 4–39. doi:10.1080/17513472.2016.1263789.
- ↑ "15.3 Hilbert's Third Problem and Dehn Theorem". Treks Into Intuitive Geometry. Springer Tokyo. 2015. pp. 382–388. doi:10.1007/978-4-431-55843-9. ISBN 9784431558415.
- ↑ Gruber, Peter M. (2007). "Chapter 16: Volume of Polytopes and Hilbert's Third Problem". Convex and Discrete Geometry. Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 336. Springer, Berlin. pp. 280–291. doi:10.1007/978-3-540-71133-9. ISBN 9783540711322.
- ↑ "On Hilbert's third problem". The Mathematical Gazette 86 (506): 241–247. July 2002. doi:10.2307/3621846.
- ↑ Skilling, John (1976). "Uniform Compounds of Uniform Polyhedra". Mathematical Proceedings of the Cambridge Philosophical Society 79 (3): 447–457. doi:10.1017/S0305004100052440. Bibcode: 1976MPCPS..79..447S.
- ↑ Hart, George (16–20 July 2019). "Bridges 2019 Conference Proceedings". Linz, Austria: Tessellations Publishing, Phoenix, Arizona. ISBN 9781938664304.
- ↑ 102.0 102.1 Yackel, Carolyn (26–30 July 2013). "Proceedings of Bridges 2009: Mathematics, Music, Art, Architecture, Culture". Banff, Alberta, Canada. pp. 123–130. ISBN 9780966520200.
- ↑ Popko, Edward S. (2012). Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere. CRC Press. pp. 100–101. ISBN 9781466504295. https://books.google.com/books?id=WLAFlr1_2S4C&pg=PA100.
- ↑ Fuller, Buckimster (1975). Synergetics: Explorations in the Geometry of Thinking. MacMillan Publishing. p. 173. ISBN 9780020653202. https://books.google.com/books?id=AKDgDQAAQBAJ&pg=PA173.
- ↑ Marat, Ton (2022). A Ludic Journey into Geometric Topology. Springer. p. 112. doi:10.1007/978-3-031-07442-4. ISBN 9783031074424. https://books.google.com/books?id=aPGGEAAAQBAJ&pg=PA112.
- ↑ Bunde, Armin; Havlin, Shlomo (2013). Fractals in Science. Springer. p. 7. ISBN 9783642779534. https://books.google.com/books?id=dh7rCAAAQBAJ&pg=PA7.
- ↑ Husain, Sakhlaq (2025). "On Jerusalem Square Fractal, Its Construction and Properties". Annals of Communications in Mathematics 8 (2): 293–298. doi:10.62072/acm.2025.080211. ISSN 2582-0818.
- ↑ Regueiro, Manuel Diaz; Allegue, Luis Diaz (July 7, 2023). "Hyperseeing: Proceedings of SMI-SCULPT 2023: Shape Modeling International 2023, Shape Creation Using Layouts, Programs, & Technology (SCULPT) Event: Twenty-second Interdisciplinary Conference of the International Society of the Arts, Mathematics, and Architecture". pp. 55-62. ISBN 9781387733309. https://hyperseeing.viz.tamu.edu/2023/title.pdf.
External links
- Weisstein, Eric W.. "Cube". http://mathworld.wolfram.com/Cube.html.
- Cube: Interactive Polyhedron Model*
- Volume of a cube, with interactive animation
- Cube (Robert Webb's site)
 |