Bienaymé's identity
From HandWiki
In probability theory, the general[1] form of Bienaymé's identity states that
- [math]\displaystyle{ \operatorname{Var}\left( \sum_{i=1}^n X_i \right)=\sum_{i=1}^n \operatorname{Var}(X_i)+2\sum_{i,j=1 \atop i \lt j}^n \operatorname{Cov}(X_i,X_j)=\sum_{i,j=1}^n\operatorname{Cov}(X_i,X_j) }[/math].
This can be simplified if [math]\displaystyle{ X_1, \ldots, X_n }[/math] are pairwise independent or just uncorrelated, integrable random variables, each with finite second moment.[2] This simplification gives:
- [math]\displaystyle{ \operatorname{Var}\left(\sum_{i=1}^n X_i\right) = \sum_{k=1}^n \operatorname{Var}(X_k) }[/math].
The above expression is sometimes referred to as Bienaymé's formula. Bienaymé's identity may be used in proving certain variants of the law of large numbers.[3]
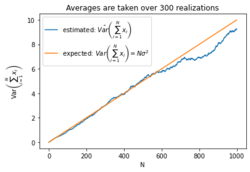
Estimated variance of the cumulative sum of iid normally distributed random variables (which could represent a gaussian random walk approximating a Wiener process). The sample variance is computed over 300 realizations of the corresponding random process.
See also
- Variance
- Propagation of error
- Markov chain central limit theorem
References
- ↑ Klenke, Achim (2013). Wahrscheinlichkeitstheorie. p. 106. doi:10.1007/978-3-642-36018-3. http://dx.doi.org/10.1007/978-3-642-36018-3.
- ↑ Loève, Michel (1977). Probability Theory I. Springer. p. 246. ISBN 3-540-90210-4.
- ↑ Itô, Kiyosi (1984). Introduction to Probability Theory. Cambridge University Press. p. 37. ISBN 0 521 26960 1.
 |

