Biography:Grégoire de Saint-Vincent

Grégoire de Saint-Vincent

Grégoire de Saint-Vincent - in Latin : Gregorius a Sancto Vincentio, in Dutch : Gregorius van St-Vincent - (8 September 1584 Bruges – 5 June 1667 Ghent) was a Flemish Jesuit and mathematician. He is remembered for his work on quadrature of the hyperbola.

Grégoire gave the "clearest early account of the summation of geometric series." He also resolved Zeno's paradox by showing that the time intervals involved formed a geometric progression and thus had a finite sum.

Life

Gregoire was born in Bruges 8 September 1584. After reading philosophy in Douai, he entered the Society of Jesus 21 October 1605. His talent was recognized by Christopher Clavius in Rome. Gregoire was sent to Louvain in 1612, and was ordained a priest 23 March 1613. Gregoire began teaching in association with François d'Aguilon in Antwerp from 1617 to 20. Moving to Louvain in 1621, he taught mathematics there until 1625. That year he became obsessed with squaring the circle and requested permission from Mutio Vitelleschi to publish his method. But Vitelleschi deferred to Christoph Grienberger, the mathematician in Rome.

On 9 September 1625, Gregoire set out for Rome to confer with Grienberger, but without avail. He returned to the Netherlands in 1627, and the following year was sent to Prague to serve in the house of Emperor Ferdinand II. After an attack of apoplexy, he was assisted there by Theodorus Moretus. When the Saxons raided Prague in 1631, Gregoire left and some of his manuscripts were lost in the mayhem. Others were returned to him in 1641 through Rodericus de Arriaga.

From 1632 Gregoire resided with The Society in Ghent and served as a mathematics teacher.

The mathematical thinking of Sancto Vincentio underwent a clear evolution during his stay in Antwerp. Starting from the problem of trisection of the angle and the determination of the two mean proportional, he made use of infinite series, the logarithmic property of the hyperbola, limits, and the related method of exhaustion. Sancto Vincentio later applied this last method, in particular to his theory ducere planum in planum, which he developed in Louvain in the years 1621 to 24.

Ductus plani in planum

Frontispiece to Saint-Vincent's Opus Geometricum

The contribution of Opus Geometricum was in

making extensive use of spatial imagery to create a multitude of solids, the volumes of which reduce to a single construction depending on the ductus of a rectilinear figure, in the absence of [algebraic notation and integral calculus] systematic geometric transformation fulfilled an essential role.

For example, the "ungula is formed by cutting a right circular cylinder by means of an oblique plane through a diameter of the circular base." And also the "’double ungula formed from cylinders with axes at right angles." Ungula was changed to "onglet" in French by Blaise Pascal when he wrote Traité des trilignes rectangles et leurs onglets.

Grégoire wrote his manuscript in the 1620s but it waited until 1647 before publication. Then it "attracted a great deal of attention...because of the systematic approach to volumetric integration developed under the name ductus plani in planum." "The construction of solids by means of two plane surfaces standing in the same ground line" is the method ductus in planum and is developed in Book VII of Opus Geometricum

In the matter of quadrature of the hyperbola, "Grégoire does everything save give explicit recognition to the relation between the area of the hyperbolic segment and the logarithm."

Quadrature of the hyperbola

[math]\displaystyle{ ln(a) }[/math] illustrated as the area under the curve [math]\displaystyle{ f(x) = 1/x }[/math] from [math]\displaystyle{ 1 }[/math] to [math]\displaystyle{ a. }[/math] If [math]\displaystyle{ a }[/math] is less than [math]\displaystyle{ 1, }[/math] the area from [math]\displaystyle{ a }[/math] to [math]\displaystyle{ 1 }[/math] is counted as negative.

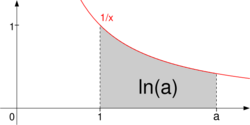
Saint-Vincent found that the area under a rectangular hyperbola (i.e. a curve given by [math]\displaystyle{ xy = k }[/math]) is the same over [math]\displaystyle{ [a,b] }[/math] as over [math]\displaystyle{ [c,d] }[/math] when

[math]\displaystyle{ \frac{a}{b} = \frac{c}{d}. }[/math]

This observation led to the hyperbolic logarithm. The stated property allows one to define a function [math]\displaystyle{ A(x) }[/math] which is the area under said curve from [math]\displaystyle{ 1 }[/math] to [math]\displaystyle{ x }[/math], which has the property that [math]\displaystyle{ A(xy) = A(x)+A(y). }[/math] This functional property characterizes logarithms, and it was mathematical fashion to call such a function [math]\displaystyle{ A(x) }[/math] a logarithm. In particular when we choose the rectangular hyperbola [math]\displaystyle{ xy = 1 }[/math], one recovers the natural logarithm.

A student and co-worker of Saint-Vincent, A. A. de Sarasa noted that this area property of the hyperbola represented a logarithm, a means of reducing multiplication to addition.

An approach to Vincent−Sarasa theorem may be seen with hyperbolic sectors and the area-invariance of squeeze mapping.

In 1651 Christiaan Huygens published his Theoremata de Quadratura Hyperboles, Ellipsis, et Circuli which referred to the work of Saint-Vincent.

The quadrature of the hyperbola was also addressed by James Gregory in 1668 in True Quadrature of Circles and Hyperbolas While Gregory acknowledged Saint-Vincent's quadrature, he devised a convergent sequence of inscribed and circumscribed areas of a general conic section for his quadrature. The term natural logarithm was introduced that year by Nicholas Mercator in his Logarithmo-technia.

Saint-Vincent was lauded as Magnan and "Learned" in 1688: “It was the great Work of the Learned Vincent or Magnan, to prove that distances reckoned in the Asymptote of an Hyperbola, in a Geometrical Progression, and the Spaces that the Perpendiculars, thereon erected, made in the Hyperbola, were equal one to the other.”

A historian of the calculus noted the assimilation of natural logarithm as an area function at that time:

As a consequence of the work of Gregory St. Vincent and de Sarasa, it seems to have been generally known in the 1660s that the area of a segment under the hyperbola [math]\displaystyle{ y = \frac{1}{x} }[/math] is proportional to the logarithm of the ratio of the ordinates at the ends of the segment.

Works

Opus geometricum posthumum, 1668

• (in la) Opus geometricum quadraturae circuli et sectionum coni decem libris comprehensum. Antwerp: Jan van Meurs & Jacob van Meurs. 1647. https://books.google.com/books?id=ptE-AAAAcAAJ. 
• (in la) Opus geometricum posthumum ad mesolabium per rationum proportionalium novas proprietates. Ghent: Bauduyn Manilius. 1668. https://gutenberg.beic.it/webclient/DeliveryManager?pid=877986. 

See also

• Gabriel's horn (1643)
• History of logarithms

References

• Karl Bopp (1907) "Die Kegelschnitte der Gregorius a St. Vincentio", Abhandlungen zum Geschichte der mathematische Wissenschaft, XX Heft.
• Christiaan Huygens (1651) Examen de la Cyclométrie du três savant Grégoire de Saint-Vincent, Oeuvres Complètes, Tome XI, link from Internet Archive.
• David Eugene Smith (1923) History of Mathematics, Ginn & Co., v.1, p. 425.
• Hans Wussing (2008) 6000 Jahre Mathematik: eine kulturgeschichtliche Zeitreise, S. 433, Springer, ISBN:9783540771920 .

External links

• Gregory Saint Vincent, and his polar coordinates from Jesuit History, Tradition and Spirituality by Joseph F. MacDonnell.
• O'Connor, John J.; Robertson, Edmund F., "Gregorius Saint-Vincent", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Saint-Vincent.html .