Biology:3-Base Periodicity Property

The DFT-method for identifying protein-coding segments of DNA

The three-base periodicity property in the field of Genomics is a property that is characteristic of protein-coding DNA sequences. The existence of this property can be shown by performing Fourier analysis on signals derived from segments of DNA sequences. Because of its predictive power, it has been used as a preliminary indicator in gene prediction.

DNA sequences are inherently signals as they are functions of an independent variable, position on the sequence. Thus, signal processing methods can be applied to them after the symbolic string is properly mapped to one (or more) numerical sequences. The reason for this periodicity is due to the biased distribution towards codon triplets, which is a consequence of genetic code degeneracy; while non-coding segments are uniformly randomly distributed and produce no significant signal in the frequency space.

History

This property has been dissected, tested and derived in a chronology of papers from different universities. The initial discovery was made in 1980 by Trifonov and Sussman who observed periodicity in DNA sequences by applying the autocorrelation function to chromatin DNA. Silverman and Linsker defined the Fourier transform of a sequence of bases, described how to "fourier analyze" it and proposed sample applications of this technique. Tsonis, Elsner and Tsonis did Fourier analysis of coding, non-coding and random sequences and proposed a reason for the 3-periodicity property found in coding sequences. Dodin proposed a method for analyzing the periodicity of DNA sequences based on the correlation function of the symbolic sequence. Tiwari, Ramachandran, Bhattacharya and Ramaswamy examined the signal-to-noise ratio of the period-3 peak within a sliding window over a sequence to identify likely coding regions.

Coding vs. Non-Coding DNA

DNA stores the information required to assemble, maintain and reproduce every living organism. A protein is a large molecule ("macromolecule") made up of smaller subunits, amino acids. DNA sequences are made up of codons, three-long nucleotide stretches, that correspond to specific amino acids. DNA creates RNA which then helps synthesize proteins. Thus, coding DNA is defined as the sections of the genome that are actually transcribed into amino acids in proteins. Noncoding DNA is sections of a DNA sequence that don't necessarily code for proteins. Identification of coding regions is important, as this information can be used in gene identification and then more generally full-genome annotation.

Formal Statement of the Property

The 3-periodicity property states that the spectral energy

[math]\displaystyle{ |S[k]|^2 = |A[k]|^2 + |T[k]|^2 + |C[k]|^2 + |G[k]|^2 }[/math]

derived from the DFT's of the four binary signals representing a DNA protein coding region of length [math]\displaystyle{ N }[/math], exhibits a peak at discrete frequency [math]\displaystyle{ k=N/3 }[/math].

Technical Details

DNA Sequences as Numerical Sequences

Formally, a DNA sequence [math]\displaystyle{ s[i] }[/math] is an ordered list of symbols from a dictionary of nucleotides [math]\displaystyle{ (A,C,T,G) }[/math]. There are multiple ways to view this as a numerical sequence, and they will all be applied to the same example:

[math]\displaystyle{ s[i] = \{A, T, G, C, A, G, C\} }[/math]

• Binary Projection

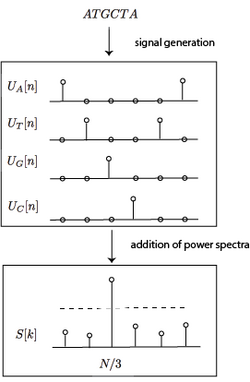
Define a binary signal for each nucleotide, [math]\displaystyle{ U_{\alpha}[i] }[/math], which is 1 when the i-th position in the sequence is the nucleotide [math]\displaystyle{ \alpha }[/math] and 0 otherwise. Formally,

[math]\displaystyle{ u_{\alpha}[i] = \begin{array}{cc} \{ & \begin{array}{cc} 1 & s[i]\, \text{is} \,\alpha\\ 0 & \text{o/w} \end{array} \end{array} }[/math]

This creates four signals which encode the position of the four nucleotides in the sequence. For the above example, the projected signals would be

ATGCAGC, [math]\displaystyle{ u_a }[/math] = 1000100, [math]\displaystyle{ u_c }[/math] = 0001001, [math]\displaystyle{ u_t }[/math] = 0100000, [math]\displaystyle{ u_g }[/math] = 0010010

• Correlation Function

Let [math]\displaystyle{ E(i,j) }[/math] be a function that is 1 if [math]\displaystyle{ s[i] = s[j] }[/math] and [math]\displaystyle{ 0 }[/math] otherwise. Let [math]\displaystyle{ c[t] = \sum_{i=t}^N E(i, i-t) }[/math]. In other words, it counts the number of times that the nucleotide at a position is equal to the nucleotide t-away on the sequence. It is invariant to changing the labeling of the bases. [math]\displaystyle{ c[0] }[/math] will always be equal to the length of the sequence. For the above example, the projected signals would be

[math]\displaystyle{ c(0) = 7 }[/math], [math]\displaystyle{ c(1) = 0 }[/math], [math]\displaystyle{ c(2) = 0 }[/math], [math]\displaystyle{ c(3) = 2 }[/math], [math]\displaystyle{ c(4) = 1 }[/math], [math]\displaystyle{ c(5) = 0 }[/math], [math]\displaystyle{ c(6) = 0 }[/math]

• Linear Map

For mathematical purposes, a gene sequence could be viewed as a signal by mapping each nucleotide into the range [1,4]. For the example above and map [math]\displaystyle{ \{A -\gt 1, T -\gt 2, C -\gt 3, G -\gt 4\} }[/math], the sequence would manifest itself as [math]\displaystyle{ 1243143 }[/math].

This process generates a single signal for the sequence, but raises questions such as which out of 24 (4!) maps should be used and what effect does this map have on our analysis. Unlike the other two mapping methods, this one is not invariant to changing the labeling of the bases but having the same structure (i.e. AACA -> TTGT), which could be detrimental for some applications.

Spectral Analysis of DNA Sequences

Once the DNA sequence has been converted into a numerical sequence, spectral analysis can be performed on that sequence. Recall the DFT is defined by the analysis equation

[math]\displaystyle{ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-2 \pi i k n / N}, }[/math]

and produces a N-long complex signal [math]\displaystyle{ X[k] }[/math] that represents the spectrum of the signal. The index [math]\displaystyle{ k }[/math] of the frequency response corresponds to an angular frequency [math]\displaystyle{ \omega }[/math] of [math]\displaystyle{ 2 \pi k / N }[/math]. For the 3-base periodicity property, the frequency content at [math]\displaystyle{ k = N / 3 }[/math] should be analyzed as it corresponds to a period of 3.

Recall that the power spectra of a sequence is equal to the magnitude of the frequency vector squared,

[math]\displaystyle{ P[k] = |X[k]|^2 }[/math]

Tiwari applied the DFT to analysis of DNA sequences using the binary projection operator. They calculated the spectra of the four projected nucleotide sequences using the DFT. Call them [math]\displaystyle{ C_{A}[k], C_{C}[k], C_{T}[k], C_{G}[k] }[/math]. Then, the power spectra of all the signals were combined,

[math]\displaystyle{ C[k] = |C_{A}[k]|^2 + |C_{C}[k]|^2 + |C_{T}[k]|^2 + |C_{G}[k]|^2. }[/math]

Then, they calculated the Signal-to-Noise ratio of this signal and performed a threshold test on that value to determine whether or not that stretch of DNA is coding.

Anti-Notch Filter

Instead of computing a Discrete Fourier Transform on different segments of the signal, the analysis can be performed in the time-domain through the use of an anti-notch filter at frequency [math]\displaystyle{ N/3 }[/math], which is much faster and performs a similar operation. An anti-notch filter applied to the signals essentially approximates the magnitude of the DFT at [math]\displaystyle{ N/3 }[/math], and a similar method is used to threshold this value to determine whether or not the window is coding or non-coding. Vaidyanathan and Yoon implemented and evaluated this method. An ideal anti-notch filter at frequency [math]\displaystyle{ N/3 }[/math] has an impulse response of

[math]\displaystyle{ h[n] = e^{2 \pi n j / 3} }[/math]

and thus the frequency content of the output of an anti-notch filtered signal is [math]\displaystyle{ X[k] = A[N/3] }[/math] if [math]\displaystyle{ k=N/3 }[/math] and 0 otherwise. By taking the magnitude of the time-domain signal, and invoking Parseval's Theorem, we get the magnitude of the frequency response. By the above logic, this is just [math]\displaystyle{ |A[N/3]|^2 }[/math] which is the quantity of interest.

Spectrograms

Spectrograms are a good way to view how the frequency content of a signal changes over time. The most common way to compute a spectrogram is to compute a Fourier transform over different segments of the signals, convert the frequency magnitude plot into an image, and concatenate those images. This is a useful way to visually identify coding and non-coding regions of DNA and to inspect other patterns that might exist.

As a Feature in Gene Identification

Identifying genes in a DNA sequence is harder than just finding what segments are coding and near impossible to identify by visually inspecting spectrograms. Genes are made up of both coding and non-coding regions, called introns and exons. Thus, the transition between coding and non-coding regions must be examined and analyzed properly to identify genes. Computing the "level" of 3-periodicity over different (possibly overlapping) windows of the sequence generates a plot of 3-periodicity over time.

These long stretches of coding vs. non-coding can then be classified as introns or exons and the entire segment heuristically labeled as gene or non-gene.

Why Can it Discriminate Coding from Non-Coding?

Binary signals can be parsed into something called a position count function (PCF), which counts the number of one's at phase [math]\displaystyle{ s }[/math] at positions that are multiples of [math]\displaystyle{ \omega }[/math]. This is expressed mathematically for a binary signal [math]\displaystyle{ A }[/math] as

[math]\displaystyle{ C_w^A (s) = \sum_{i=0}^{\frac{N-1}{\omega}} A[\omega i + s]. }[/math]

For [math]\displaystyle{ \omega=3 }[/math], there are three PCFs [math]\displaystyle{ (C_3^A(0) }[/math], [math]\displaystyle{ C_3^A(1) }[/math] and [math]\displaystyle{ C_3^A(2)) }[/math] which each count the number of one's at positions [math]\displaystyle{ \{0,3,6,...\} }[/math], [math]\displaystyle{ \{1,4,7,...\} }[/math], [math]\displaystyle{ \{2,5,8,...\} }[/math] respectively. It can be shown that the magnitude of the DFT at [math]\displaystyle{ N/3 }[/math] is in fact directly related to the PCF and is equal to

[math]\displaystyle{ |\tilde{A}[N/3]|^2 = \frac{1}{2} [(C_3^A(0) - C_3^A(1))^2 + (C_3^A(1) - C_3^A(2))^2 + (C_3^A(2) - C_3^A(0))^2]. }[/math]

In other words, the spectral power at [math]\displaystyle{ N/3 }[/math] in the DFT depends only on the difference between the PCFs at different phases. This relation here is the fundamental to the explanation for why this method can identify coding regions. This is because the spectral power at [math]\displaystyle{ N/3 }[/math] will be determined by how the codons that make up the sequence are sampled.

If the codons are sampled uniformly at random, as they would be in a noncoding segment of DNA, there is a high chance that the PCFs would not differ by a significant amount and the power at that frequency will be low.

However, in a protein-coding sequence, the DNA sequence is made up of a string of codons which correspond to amino acids. Because the genetic code is degenerate (more than one codon map to a single amino acid) and samples from the amino acids rather than the codons, the codons are not sampled uniformly thus leading to differences in the PCFs.

There is also empirical evidence for why this method works. In other words, over multiple studies this method has been able to discriminate coding vs. non-coding DNA segments. These are discussed in the next section.

Experiments

This method has been applied to sequence data from a number of organisms, details of which can be found in the references section. A few will be summarized here.

Tiwari, who wrote the paper to first apply DFT to analyzing periodicity of DNA sequences, applied this method to S.cerevisiae and H.influenzuae. For S.cerevisiae, they were able to locate 413 out of 483 probable genes (ORFs). For H.influenzuae, they were able to locate 167 out of 194 identified genes. In both studies, they had a zero false-positive rate.

Datta and Asif analyzed the algorithm's ability to identify coding regions of different lengths in chromosome III of C. elegans. Longer coding sequences are detected with higher probability. This seems to be a consequence of the Uncertainty principle (shorter-time signals spread out in frequency content) and the fact that fewer codons are provided in shorter sequences.

Pros and Cons of the Property

Pros

• Requires no training data

The method can be run on any DNA sequence, where as other methods such as BLAST, FASTA and Smith-Waterman require empirical data.

• Independent of variations in base compositions

This is because the total spectral power is

[math]\displaystyle{ |S[k]|^2 = |A[k]|^2 + |T[k]^2 + |C[k]|^2 + |G[k]|^2, }[/math]

and no one base contributes more than another.

• Low false-positive rate
• Robust to sequencing errors resulting in frameshifts

This is due to the property that shifting a sequence does not change the magnitude of its Discrete Fourier Transform.

[math]\displaystyle{ x[n-n_0] \leftrightarrow X[k] e^{-j 2 \pi k n_0 / N} }[/math]

[math]\displaystyle{ |X[k] e^{-j 2 \pi k n_0 / N}| = |X[k]| }[/math]

Cons

• Three-base periodicity found to be lacking in some genes
• Outperformed by modern empirical and specialized gene prediction methods