Biology:Double Cut and Join Model

A, B: Two genomes with four synteny blocks. C: The adjacency graph of the genomes pictured in A and B.

The double cut and join (DCJ) model is a model for genome rearrangement used to define an edit distance between genomes based on gene order and orientation, rather than nucleotide sequence. It takes the fundamental units of a genome to be synteny blocks, maximal sections of DNA conserved between genomes. It focuses on changes due to genome rearrangement operations such as inversions, translocations as well as the creation and absorption of circular intermediates.

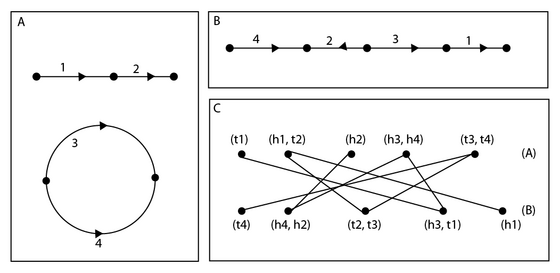
A genome is described as a directed, edge labeled graph with each vertex having degree 1 or 2. Edges are labeled as synteny blocks, vertices of degree 1 represent telomeres, and vertices of degree 2 representing adjacencies between blocks. This requires that the genome consist of cycles and paths. Each component is called a chromosome. The beginning of each edge is called the tail, the end of each edge is called the head; together heads and tails are known as extremities. Vertices are described by their roles as heads and tails of blocks, for instance, in the figure, the adjacency which forms the head of marker 1 and the tail of marker 2 is labelled (h1, t2), the telomere formed by the head of 2 is (h2). A double cut and join (DCJ) operation consists of one of the following four transformations:

• (i) breaking two adjacencies (a, b) and (c, d) to create two more adjacencies, (a, c) and (b,d)
• (ii) taking an adjacency (a, b) and a telomere (c) to create a new adjacency and telomere, either as (a, c), (b) or (b,c), (a).
• (iii) taking two telomeres (a) and (b) and creating a new adjacency (a, b)
• (iv) breaking an adjacency (a, b) to create the two telomeres (a) and (b).

An edit distance, the double cut and join distance, is defined between genomes with the same number of edges [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math], [math]\displaystyle{ d_{DCJ}(A, B) }[/math] as the minimum number of DCJ operations needed to transform [math]\displaystyle{ A }[/math] into [math]\displaystyle{ B }[/math].

Mathematical Results

The DCJ distance defines a metric space. To verify this, we first note that [math]\displaystyle{ d_{DCJ}(G, G)=0 }[/math], since no operations are needed to change G into itself, and if [math]\displaystyle{ G_1\neq G_2 }[/math], [math]\displaystyle{ d_{DCJ}(G_1, G_2)\gt 0 }[/math], since at least one operation is needed to transform [math]\displaystyle{ G_1 }[/math] into any other genome. (A proof that the [math]\displaystyle{ d_{DCJ}(G_1, G_2) }[/math] is always defined whenever [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] are genomes with the same edges will follow.) Note that each operation has an inverse: (i) and (ii) are their own inverses, and (iii) is the inverse of (iv). Thus [math]\displaystyle{ d_{DCJ}(G_1, G_2)=d_{DCJ}(G_2, G_1) }[/math]. The triangle inequality [math]\displaystyle{ d_{DCJ}(G_1, G_3)\leq d_{DCJ}(G_1, G_2)+d_{DCJ}(G_2, G_3) }[/math] holds because a series of DCJ operations transforming [math]\displaystyle{ G_1 }[/math] to [math]\displaystyle{ G_2 }[/math] followed by a series of transformations from [math]\displaystyle{ G_2 }[/math] to [math]\displaystyle{ G_3 }[/math] will transform [math]\displaystyle{ G_1 }[/math] to [math]\displaystyle{ G_3 }[/math], so the minimal number of operations needed to transform [math]\displaystyle{ G_1 }[/math] to [math]\displaystyle{ G_3 }[/math] must be no longer than this.

To compute the DCJ distance between two genomes [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] with the same set of synteny blocks, we construct a bipartite multigraph known as the adjacency graph [math]\displaystyle{ A=(V(G_1), V(G_2), E) }[/math] of the genomes. The vertex set of the adjacency graph is [math]\displaystyle{ (V(G_1), V(G_2)) }[/math], where [math]\displaystyle{ V(G_1) }[/math] is the vertex set of [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ V(G_2) }[/math] is the vertex set of [math]\displaystyle{ G_2 }[/math]. For [math]\displaystyle{ a\in V(G_1) }[/math] and [math]\displaystyle{ b\in V(G_2) }[/math], we have [math]\displaystyle{ (a, b)\in E }[/math] if [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] are an extremity of the same synteny block. If [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] share two extremities, we add two edges between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] to [math]\displaystyle{ G }[/math].

If [math]\displaystyle{ A=B }[/math], we see that the adjacency graph is composed entirely of paths of length 1, connecting two telomeres, and cycles of length 2, connecting two adjacencies. We can use this fact to calculate [math]\displaystyle{ d_{DCJ} }[/math][math]\displaystyle{ }[/math]. Let [math]\displaystyle{ N }[/math] be the number of synteny blocks in genomes [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math], [math]\displaystyle{ C }[/math] be the number of cycles in their adjacency graph, and [math]\displaystyle{ I }[/math] be the number of paths in their adjacency graph. Then [math]\displaystyle{ d_{DCJ}(G_1, G_2)=N-(C+1/2). }[/math] The proof shows that each DCJ operation can decrease [math]\displaystyle{ N-(C+1/2) }[/math] by no more than 1, and that if [math]\displaystyle{ G_1\neq G_2 }[/math], there exists an operation decreasing [math]\displaystyle{ N-(C+I/2). }[/math]. This proves that [math]\displaystyle{ d_{DCJ} }[/math] is always defined, and gives a method for its calculation. Since it is easy to count cycles and paths, [math]\displaystyle{ d_{DCJ} }[/math] can be found in linear time.