Triangle inequality

Short description: Property of geometry, also used to generalize the notion of "distance" in metric spaces

Three examples of the triangle inequality for triangles with sides of lengths

x

,

y

,

z

. The top example shows a case where

z

is much less than the sum

x + y

of the other two sides, and the bottom example shows a case where the side

z

is only slightly less than

x + y

.

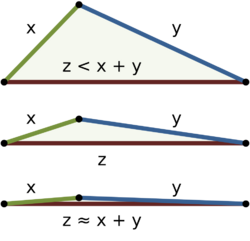
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side.^[1]^[2] This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality.^[3] If $x$ , $y$ , and $z$ are the lengths of the sides of the triangle, with no side being greater than $z$ , then the triangle inequality states that

[math]\displaystyle{ z \leq x + y , }[/math]

with equality only in the degenerate case of a triangle with zero area.

In Euclidean geometry and some other geometries, the triangle inequality is a theorem about distances, and it is written using vectors and vector lengths (norms):

[math]\displaystyle{ \|\mathbf x + \mathbf y\| \leq \|\mathbf x\| + \|\mathbf y\| , }[/math]

where the length $z$ of the third side has been replaced by the vector sum $x + y$ . When $x$ and $y$ are real numbers, they can be viewed as vectors in [math]\displaystyle{ \R^1 }[/math], and the triangle inequality expresses a relationship between absolute values.

In Euclidean geometry, for right triangles the triangle inequality is a consequence of the Pythagorean theorem, and for general triangles, a consequence of the law of cosines, although it may be proved without these theorems. The inequality can be viewed intuitively in either [math]\displaystyle{ \R^2 }[/math] or [math]\displaystyle{ \R^3 }[/math]. The figure at the right shows three examples beginning with clear inequality (top) and approaching equality (bottom). In the Euclidean case, equality occurs only if the triangle has a $180°$ angle and two $0°$ angles, making the three vertices collinear, as shown in the bottom example. Thus, in Euclidean geometry, the shortest distance between two points is a straight line.

In spherical geometry, the shortest distance between two points is an arc of a great circle, but the triangle inequality holds provided the restriction is made that the distance between two points on a sphere is the length of a minor spherical line segment (that is, one with central angle in $[0, π]$ ) with those endpoints.^[4]^[5]

The triangle inequality is a defining property of norms and measures of distance. This property must be established as a theorem for any function proposed for such purposes for each particular space: for example, spaces such as the real numbers, Euclidean spaces, the L^p spaces ( $p \geq 1$ ), and inner product spaces.

Euclidean geometry

Euclid's construction for proof of the triangle inequality for plane geometry.

Euclid proved the triangle inequality for distances in plane geometry using the construction in the figure.^[6] Beginning with triangle $ABC$ , an isosceles triangle is constructed with one side taken as $BC$ and the other equal leg $BD$ along the extension of side $AB$ . It then is argued that angle $β$ has larger measure than angle $α$ , so side $AD$ is longer than side $AC$ . However:

[math]\displaystyle{ \overline{AD} = \overline{AB} + \overline{BD} = \overline{AB} + \overline{BC}, }[/math]

so the sum of the lengths of sides $AB$ and $BC$ is larger than the length of $AC$ . This proof appears in Euclid's Elements, Book 1, Proposition 20.^[7]

Mathematical expression of the constraint on the sides of a triangle

For a proper triangle, the triangle inequality, as stated in words, literally translates into three inequalities (given that a proper triangle has side lengths $a, b, c$ that are all positive and excludes the degenerate case of zero area):

[math]\displaystyle{ a + b \gt c ,\quad b + c \gt a ,\quad c + a \gt b . }[/math]

A more succinct form of this inequality system can be shown to be

[math]\displaystyle{ |a - b| \lt c \lt a + b . }[/math]

Another way to state it is

[math]\displaystyle{ \max(a, b, c) \lt a + b + c - \max(a, b, c) }[/math]

implying

[math]\displaystyle{ 2 \max(a, b, c) \lt a + b + c }[/math]

and thus that the longest side length is less than the semiperimeter.

A mathematically equivalent formulation is that the area of a triangle with sides $a, b, c$ must be a real number greater than zero. Heron's formula for the area is

[math]\displaystyle{ \begin{align} 4\cdot \text{area} & =\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)} \\ & = \sqrt{-a^4-b^4-c^4+2a^2b^2+2a^2c^2+2b^2c^2}. \end{align} }[/math]

In terms of either area expression, the triangle inequality imposed on all sides is equivalent to the condition that the expression under the square root sign be real and greater than zero (so the area expression is real and greater than zero).

The triangle inequality provides two more interesting constraints for triangles whose sides are $a, b, c$ , where $a \geq b \geq c$ and [math]\displaystyle{ \phi }[/math] is the golden ratio, as

[math]\displaystyle{ 1\lt \frac{a+c}{b}\lt 3 }[/math]

[math]\displaystyle{ 1\le\min\left(\frac{a}{b}, \frac{b}{c}\right)\lt \phi. }[/math]^[8]

Right triangle

Isosceles triangle with equal sides

AB = AC

divided into two right triangles by an altitude drawn from one of the two base angles.

In the case of right triangles, the triangle inequality specializes to the statement that the hypotenuse is greater than either of the two sides and less than their sum.^[9]

The second part of this theorem is already established above for any side of any triangle. The first part is established using the lower figure. In the figure, consider the right triangle $ADC$ . An isosceles triangle $ABC$ is constructed with equal sides $AB = AC$ . From the triangle postulate, the angles in the right triangle $ADC$ satisfy:

[math]\displaystyle{ \alpha + \gamma = \pi /2 \ . }[/math]

Likewise, in the isosceles triangle $ABC$ , the angles satisfy:

[math]\displaystyle{ 2\beta + \gamma = \pi \ . }[/math]

Therefore,

[math]\displaystyle{ \alpha = \pi/2 - \gamma ,\ \mathrm{while} \ \beta= \pi/2 - \gamma /2 \ , }[/math]

and so, in particular,

[math]\displaystyle{ \alpha \lt \beta \ . }[/math]

That means side $AD$ , which is opposite to angle $α$ , is shorter than side $AB$ , which is opposite to the larger angle $β$ . But $AB = AC$ . Hence:

[math]\displaystyle{ \overline{AC} \gt \overline{AD} \ . }[/math]

A similar construction shows $AC > DC$ , establishing the theorem.

An alternative proof (also based upon the triangle postulate) proceeds by considering three positions for point $B$ :^[10] (i) as depicted (which is to be proved), or (ii) $B$ coincident with $D$ (which would mean the isosceles triangle had two right angles as base angles plus the vertex angle $γ$ , which would violate the triangle postulate), or lastly, (iii) $B$ interior to the right triangle between points $A$ and $D$ (in which case angle $ABC$ is an exterior angle of a right triangle $BDC$ and therefore larger than $π /2$ , meaning the other base angle of the isosceles triangle also is greater than $π /2$ and their sum exceeds $π$ in violation of the triangle postulate).

This theorem establishing inequalities is sharpened by Pythagoras' theorem to the equality that the square of the length of the hypotenuse equals the sum of the squares of the other two sides.

Examples of use

Consider a triangle whose sides are in an arithmetic progression and let the sides be $a, a + d, a + 2 d$ . Then the triangle inequality requires that

[math]\displaystyle{ \begin{array}{rcccl} 0 &\lt & a &\lt & 2a+3d, \\ 0 &\lt & a+d &\lt & 2a+2d, \\ 0 &\lt & a+2d &\lt & 2a+d. \end{array} }[/math]

To satisfy all these inequalities requires

[math]\displaystyle{ a\gt 0 \text{ and } -\frac{a}{3}\lt d\lt a. }[/math]^[11]

When $d$ is chosen such that $d = a /3$ , it generates a right triangle that is always similar to the Pythagorean triple with sides $3$ , $4$ , $5$ .

Now consider a triangle whose sides are in a geometric progression and let the sides be $a, ar, ar 2$ . Then the triangle inequality requires that

[math]\displaystyle{ \begin{array}{rcccl} 0 &\lt & a &\lt & ar+ar^2, \\ 0 &\lt & ar &\lt & a+ar^2, \\ 0 &\lt & \! ar^2 &\lt & a+ar. \end{array} }[/math]

The first inequality requires $a > 0$ ; consequently it can be divided through and eliminated. With $a > 0$ , the middle inequality only requires $r > 0$ . This now leaves the first and third inequalities needing to satisfy

[math]\displaystyle{ \begin{align} r^2+r-1 & {} \gt 0 \\ r^2-r-1 & {} \lt 0. \end{align} }[/math]

The first of these quadratic inequalities requires $r$ to range in the region beyond the value of the positive root of the quadratic equation $r 2 + r - 1 = 0$ , i.e. $r > φ - 1$ where $φ$ is the golden ratio. The second quadratic inequality requires $r$ to range between 0 and the positive root of the quadratic equation $r 2 - r - 1 = 0$ , i.e. $0 < r < φ$ . The combined requirements result in $r$ being confined to the range

[math]\displaystyle{ \varphi - 1 \lt r \lt \varphi\, \text{ and } a \gt 0. }[/math]^[12]

When $r$ the common ratio is chosen such that $r = \sqrt φ$ it generates a right triangle that is always similar to the Kepler triangle.

Generalization to any polygon

The triangle inequality can be extended by mathematical induction to arbitrary polygonal paths, showing that the total length of such a path is no less than the length of the straight line between its endpoints. Consequently, the length of any polygon side is always less than the sum of the other polygon side lengths.

Example of the generalized polygon inequality for a quadrilateral

Consider a quadrilateral whose sides are in a geometric progression and let the sides be $a, ar, ar 2, ar 3$ . Then the generalized polygon inequality requires that

[math]\displaystyle{ \begin{array}{rcccl} 0 &\lt & a &\lt & ar+ar^2+ar^3 \\ 0 &\lt & ar &\lt & a+ar^2+ar^3 \\ 0 &\lt & ar^2 &\lt & a+ar+ar^3 \\ 0 &\lt & ar^3 &\lt & a+ar+ar^2. \end{array} }[/math]

These inequalities for $a > 0$ reduce to the following

[math]\displaystyle{ r^3+r^2+r-1\gt 0 }[/math]

[math]\displaystyle{ r^3-r^2-r-1\lt 0. }[/math]^[13]

The left-hand side polynomials of these two inequalities have roots that are the tribonacci constant and its reciprocal. Consequently, $r$ is limited to the range $1/ t < r < t$ where $t$ is the tribonacci constant.

Relationship with shortest paths

The arc length of a curve is defined as the least upper bound of the lengths of polygonal approximations.

This generalization can be used to prove that the shortest curve between two points in Euclidean geometry is a straight line.

No polygonal path between two points is shorter than the line between them. This implies that no curve can have an arc length less than the distance between its endpoints. By definition, the arc length of a curve is the least upper bound of the lengths of all polygonal approximations of the curve. The result for polygonal paths shows that the straight line between the endpoints is the shortest of all the polygonal approximations. Because the arc length of the curve is greater than or equal to the length of every polygonal approximation, the curve itself cannot be shorter than the straight line path.^[14]

Converse

The converse of the triangle inequality theorem is also true: if three real numbers are such that each is less than the sum of the others, then there exists a triangle with these numbers as its side lengths and with positive area; and if one number equals the sum of the other two, there exists a degenerate triangle (that is, with zero area) with these numbers as its side lengths.

In either case, if the side lengths are $a$ , $b$ , $c$ we can attempt to place a triangle in the Euclidean plane as shown in the diagram. We need to prove that there exists a real number $h$ consistent with the values $a$ , $b$ , and $c$ , in which case this triangle exists.

Triangle with altitude

h

cutting base

c

into

d + (c - d)

.

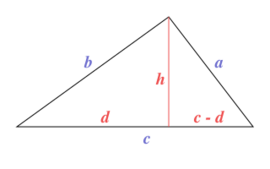
By the Pythagorean theorem we have $b 2 = h 2 + d 2$ and $a 2 = h 2 + (c - d) 2$ according to the figure at the right. Subtracting these yields $a 2 - b 2 = c 2 - 2 cd$ . This equation allows us to express $d$ in terms of the sides of the triangle:

[math]\displaystyle{ d=\frac{-a^2+b^2+c^2}{2c}. }[/math]

For the height of the triangle we have that $h 2 = b 2 - d 2$ . By replacing $d$ with the formula given above, we have

[math]\displaystyle{ h^2 = b^2-\left(\frac{-a^2+b^2+c^2}{2c}\right)^2. }[/math]

For a real number $h$ to satisfy this, $h 2$ must be non-negative:

[math]\displaystyle{ \begin{align} 0 &\le b^2-\left(\frac{-a^2+b^2+c^2}{2c}\right)^2 \\[4pt] 0 &\le \left(b- \frac{-a^2+b^2+c^2}{2c}\right) \left(b + \frac{-a^2+b^2+c^2}{2c}\right) \\[4pt] 0 &\le \left(a^2-(b-c)^2)((b+c)^2-a^2 \right) \\[6pt] 0 &\le (a+b-c)(a-b+c)(b+c+a)(b+c-a) \\[6pt] 0 &\le (a+b-c)(a+c-b)(b+c-a) \end{align} }[/math]

which holds if the triangle inequality is satisfied for all sides. Therefore, there does exist a real number [math]\displaystyle{ h }[/math] consistent with the sides [math]\displaystyle{ a, b, c }[/math], and the triangle exists. If each triangle inequality holds strictly, [math]\displaystyle{ h \gt 0 }[/math] and the triangle is non-degenerate (has positive area); but if one of the inequalities holds with equality, so [math]\displaystyle{ h = 0 }[/math], the triangle is degenerate.

Generalization to higher dimensions

The area of a triangular face of a tetrahedron is less than or equal to the sum of the areas of the other three triangular faces. More generally, in Euclidean space the hypervolume of an $(n - 1)$ -facet of an $n$ -simplex is less than or equal to the sum of the hypervolumes of the other $n$ facets.

Much as the triangle inequality generalizes to a polygon inequality, the inequality for a simplex of any dimension generalizes to a polytope of any dimension: the hypervolume of any facet of a polytope is less than or equal to the sum of the hypervolumes of the remaining facets.

In some cases the tetrahedral inequality is stronger than several applications of the triangle inequality. For example, the triangle inequality appears to allow the possibility of four points $A$ , $B$ , $C$ , and $Z$ in Euclidean space such that distances

AB = BC = CA = 26

and

AZ = BZ = CZ = 14

.

However, points with such distances cannot exist: the area of the 26–26–26 equilateral triangle $ABC$ is $169 \sqrt 3$ , which is larger than three times $39 \sqrt 3$ , the area of a 26–14–14 isosceles triangle (all by Heron's formula), and so the arrangement is forbidden by the tetrahedral inequality.

Normed vector space

Triangle inequality for norms of vectors.

In a normed vector space $V$ , one of the defining properties of the norm is the triangle inequality:

[math]\displaystyle{ \|x + y\| \leq \|x\| + \|y\| \quad \forall \, x, y \in V }[/math]

that is, the norm of the sum of two vectors is at most as large as the sum of the norms of the two vectors. This is also referred to as subadditivity. For any proposed function to behave as a norm, it must satisfy this requirement.^[15]

If the normed space is Euclidean, or, more generally, strictly convex, then [math]\displaystyle{ \|x+y\|=\|x\|+\|y\| }[/math] if and only if the triangle formed by $x$ , $y$ , and $x + y$ , is degenerate, that is, $x$ and $y$ are on the same ray, i.e., $x = 0$ or $y = 0$ , or $x = α y$ for some $α > 0$ . This property characterizes strictly convex normed spaces such as the $ℓ p$ spaces with $1 < p < \infty$ . However, there are normed spaces in which this is not true. For instance, consider the plane with the $ℓ 1$ norm (the Manhattan distance) and denote $x = (1, 0)$ and $y = (0, 1)$ . Then the triangle formed by $x$ , $y$ , and $x + y$ , is non-degenerate but

[math]\displaystyle{ \|x+y\|=\|(1,1)\|=|1|+|1|=2=\|x\|+\|y\|. }[/math]

Example norms

Absolute value as norm for the real line. To be a norm, the triangle inequality requires that the absolute value satisfy for any real numbers $x$ and $y$ : [math]\displaystyle{ |x + y| \leq |x|+|y|, }[/math] which it does.

Proof:^[16]

[math]\displaystyle{ -\left\vert x \right\vert \leq x \leq \left\vert x \right\vert }[/math]

[math]\displaystyle{ -\left\vert y \right\vert \leq y \leq \left\vert y \right\vert }[/math]

After adding,

[math]\displaystyle{ -( \left\vert x \right\vert + \left\vert y \right\vert ) \leq x+y \leq \left\vert x \right\vert + \left\vert y \right\vert }[/math]

Use the fact that [math]\displaystyle{ \left\vert b \right\vert \leq a \Leftrightarrow -a \leq b \leq a }[/math] (with $b$ replaced by $x + y$ and $a$ by [math]\displaystyle{ \left\vert x \right\vert + \left\vert y \right\vert }[/math]), we have

[math]\displaystyle{ |x + y| \leq |x|+|y| }[/math]

The triangle inequality is useful in mathematical analysis for determining the best upper estimate on the size of the sum of two numbers, in terms of the sizes of the individual numbers.

There is also a lower estimate, which can be found using the reverse triangle inequality which states that for any real numbers $x$ and $y$ :

[math]\displaystyle{ |x-y| \geq \biggl||x|-|y|\biggr|. }[/math]

Inner product as norm in an inner product space. If the norm arises from an inner product (as is the case for Euclidean spaces), then the triangle inequality follows from the Cauchy–Schwarz inequality as follows: Given vectors [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math], and denoting the inner product as [math]\displaystyle{ \langle x , y\rangle }[/math]:^[17]

[math]\displaystyle{ \\|x + y\\|^2 }[/math]	[math]\displaystyle{ = \langle x + y, x + y \rangle }[/math]
	[math]\displaystyle{ = \\|x\\|^2 + \langle x, y \rangle + \langle y, x \rangle + \\|y\\|^2 }[/math]
	[math]\displaystyle{ \le \\|x\\|^2 + 2\|\langle x, y \rangle\| + \\|y\\|^2 }[/math]
	[math]\displaystyle{ \le \\|x\\|^2 + 2\\|x\\|\\|y\\| + \\|y\\|^2 }[/math] (by the Cauchy–Schwarz inequality)
	[math]\displaystyle{ = \left(\\|x\\| + \\|y\\|\right)^2 }[/math].

The Cauchy–Schwarz inequality turns into an equality if and only if $x$ and $y$ are linearly dependent. The inequality [math]\displaystyle{ \langle x, y \rangle + \langle y, x \rangle \le 2\left|\left\langle x, y \right\rangle\right| }[/math] turns into an equality for linearly dependent [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] if and only if one of the vectors $x$ or $y$ is a nonnegative scalar of the other.

Taking the square root of the final result gives the triangle inequality.

$p$ -norm: a commonly used norm is the $p$ -norm: [math]\displaystyle{ \|x\|_p = \left( \sum_{i=1}^n |x_i|^p \right) ^{1/p} \ , }[/math] where the $x i$ are the components of vector $x$ . For $p = 2$ the $p$ -norm becomes the Euclidean norm: [math]\displaystyle{ \|x\|_2 = \left( \sum_{i=1}^n |x_i|^2 \right) ^{1/2} = \left( \sum_{i=1}^n x_{i}^2 \right) ^{1/2} \ , }[/math] which is Pythagoras' theorem in $n$ -dimensions, a very special case corresponding to an inner product norm. Except for the case $p = 2$ , the $p$ -norm is not an inner product norm, because it does not satisfy the parallelogram law. The triangle inequality for general values of $p$ is called Minkowski's inequality.^[18] It takes the form:[math]\displaystyle{ \|x+y\|_p \le \|x\|_p + \|y\|_p \ . }[/math]

Metric space

In a metric space $M$ with metric $d$ , the triangle inequality is a requirement upon distance:

[math]\displaystyle{ d(x,\ z) \le d(x,\ y) + d(y,\ z) \ , }[/math]

for all $x$ , $y$ , $z$ in $M$ . That is, the distance from $x$ to $z$ is at most as large as the sum of the distance from $x$ to $y$ and the distance from $y$ to $z$ .

The triangle inequality is responsible for most of the interesting structure on a metric space, namely, convergence. This is because the remaining requirements for a metric are rather simplistic in comparison. For example, the fact that any convergent sequence in a metric space is a Cauchy sequence is a direct consequence of the triangle inequality, because if we choose any $x n$ and $x m$ such that $d (x n, x) < ε /2$ and $d (x m, x) < ε /2$ , where $ε > 0$ is given and arbitrary (as in the definition of a limit in a metric space), then by the triangle inequality, $d (x n, x m) \leq d (x n, x) + d (x m, x) < ε /2 + ε /2 = ε$ , so that the sequence ${x n}$ is a Cauchy sequence, by definition.

This version of the triangle inequality reduces to the one stated above in case of normed vector spaces where a metric is induced via $d (x, y) ≔ ‖ x - y ‖$ , with $x - y$ being the vector pointing from point $y$ to $x$ .

Reverse triangle inequality

The reverse triangle inequality is a logically equivalent alternative formulation of the triangle inequality that gives lower bounds instead of upper bounds. For plane geometry, the statement is:^[19]

Any side of a triangle is greater than or equal to the difference between the other two sides.

In the case of a normed vector space, the statement is:

[math]\displaystyle{ \bigg|\|x\|-\|y\|\bigg| \leq \|x-y\|, }[/math]

or for metric spaces, [math]\displaystyle{ |d(x, z) - d(y, z)| \leq d(x, y) }[/math]. This implies that the norm [math]\displaystyle{ \|\cdot\| }[/math] as well as the distance-from-[math]\displaystyle{ z }[/math] function [math]\displaystyle{ d(z ,\cdot) }[/math] are Lipschitz continuous with Lipschitz constant $1$ , and therefore are in particular uniformly continuous.

The proof of the reverse triangle inequality from the usual one uses [math]\displaystyle{ \|y-x\| = \|{-}1(x-y)\| = |{-}1|\cdot\|x-y\| = \|x-y\| }[/math] to find:

[math]\displaystyle{ \|x\| = \|(x-y) + y\| \leq \|x-y\| + \|y\| \Rightarrow \|x\| - \|y\| \leq \|x-y\|, }[/math]

[math]\displaystyle{ \|y\| = \|(y-x) + x\| \leq \|y-x\| + \|x\| \Rightarrow \|x\| - \|y\| \geq -\|x-y\|, }[/math]

Combining these two statements gives:

[math]\displaystyle{ -\|x-y\| \leq \|x\|-\|y\| \leq \|x-y\| \Rightarrow \bigg|\|x\|-\|y\|\bigg| \leq \|x-y\|. }[/math]

In the converse, the proof of the triangle inequality from the reverse triangle inequality works in two cases:

If [math]\displaystyle{ \|x +y\| - \|x\| \geq 0, }[/math] then by the reverse triangle inequality, [math]\displaystyle{ \|x +y\| - \|x\| = {\bigg|}\|x + y\|-\|x\|{\bigg|} \leq \|(x + y) - x\| = \|y\| \Rightarrow \|x + y\| \leq \|x\| + \|y\| }[/math],

and if [math]\displaystyle{ \|x +y\| - \|x\| \lt 0, }[/math] then trivially [math]\displaystyle{ \|x\| +\|y\| \geq \|x\| \gt \|x + y\| }[/math] by the nonnegativity of the norm.

Thus, in both cases, we find that [math]\displaystyle{ \|x\| + \|y\| \geq \|x + y\| }[/math].

For metric spaces, the proof of the reverse triangle inequality is found similarly by:

[math]\displaystyle{ d(x, y) + d(y, z) \geq d(x, z) \Rightarrow d(x, y) \geq d(x, z) - d(y, z) }[/math]

[math]\displaystyle{ d(z, x) + d(x, y) \geq d(z, y) \Rightarrow d(x, y) \geq d(y, z) - d(x, z) }[/math]

Putting these equations together we find:

[math]\displaystyle{ d(x, y) \geq |d(x, z) - d(y, z)| }[/math]

And in the converse, beginning from the reverse triangle inequality, we can again use two cases:

If [math]\displaystyle{ d(x, z) - d(y, z) \geq 0 }[/math], then [math]\displaystyle{ d(x, y) \geq |d(x, z) - d(y, z)| = d(x, z) - d(y, z) \Rightarrow d(x, y) + d(y, z) \geq d(x, z) }[/math],

and if [math]\displaystyle{ d(x, z) - d(y, z) \lt 0, }[/math] then [math]\displaystyle{ d(x, y) + d(y, z) \geq d(y, z) \gt d(x, z) }[/math] again by the nonnegativity of the metric.

Thus, in both cases, we find that [math]\displaystyle{ d(x, y) + d(y, z) \geq d(x, z) }[/math].

Triangle inequality for cosine similarity

By applying the cosine function to the triangle inequality and reverse triangle inequality for arc lengths and employing the angle addition and subtraction formulas for cosines, it follows immediately that

[math]\displaystyle{ \operatorname{sim}(x,z) \geq \operatorname{sim}(x,y) \cdot \operatorname{sim}(y,z) - \sqrt{\left(1-\operatorname{sim}(x,y)^2\right)\cdot\left(1-\operatorname{sim}(y,z)^2\right)} }[/math]

and

[math]\displaystyle{ \operatorname{sim}(x,z) \leq \operatorname{sim}(x,y) \cdot \operatorname{sim}(y,z) + \sqrt{\left(1-\operatorname{sim}(x,y)^2\right)\cdot\left(1-\operatorname{sim}(y,z)^2\right)}\,. }[/math]

With these formulas, one needs to compute a square root for each triple of vectors ${x, y, z}$ that is examined rather than $arccos(sim(x, y))$ for each pair of vectors ${x, y}$ examined, and could be a performance improvement when the number of triples examined is less than the number of pairs examined.

Reversal in Minkowski space

The Minkowski space metric [math]\displaystyle{ \eta_{\mu \nu} }[/math] is not positive-definite, which means that [math]\displaystyle{ \|x\|^2 = \eta_{\mu \nu} x^\mu x^\nu }[/math] can have either sign or vanish, even if the vector $x$ is non-zero. Moreover, if $x$ and $y$ are both timelike vectors lying in the future light cone, the triangle inequality is reversed:

[math]\displaystyle{ \|x+y\| \geq \|x\| + \|y\|. }[/math]

A physical example of this inequality is the twin paradox in special relativity. The same reversed form of the inequality holds if both vectors lie in the past light cone, and if one or both are null vectors. The result holds in [math]\displaystyle{ n + 1 }[/math] dimensions for any [math]\displaystyle{ n \geq 1 }[/math]. If the plane defined by [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] is space-like (and therefore a Euclidean subspace) then the usual triangle inequality holds.

Notes

↑ Wolfram MathWorld – http://mathworld.wolfram.com/TriangleInequality.html
↑ Mohamed A. Khamsi; William A. Kirk (2001). "§1.4 The triangle inequality in $R n$ ". An introduction to metric spaces and fixed point theory. Wiley-IEEE. ISBN 0-471-41825-0. https://books.google.com/books?id=4qXbEpAK5eUC&pg=PA8.
↑ for instance, Jacobs, Harold R. (1974), Geometry, W. H. Freeman & Co., p. 246, ISBN 0-7167-0456-0
↑ Oliver Brock; Jeff Trinkle; Fabio Ramos (2009). Robotics: Science and Systems IV. MIT Press. p. 195. ISBN 978-0-262-51309-8. https://books.google.com/books?id=fvCaQfBQ7qEC&pg=PA195.
↑ Arlan Ramsay; Robert D. Richtmyer (1995). Introduction to hyperbolic geometry. Springer. p. 17. ISBN 0-387-94339-0. https://archive.org/details/introductiontohy0000rams.
↑ Harold R. Jacobs (2003). Geometry: seeing, doing, understanding (3rd ed.). Macmillan. p. 201. ISBN 0-7167-4361-2. https://books.google.com/books?id=XhQRgZRDDq0C&pg=PA201.
↑ David E. Joyce (1997). "Euclid's elements, Book 1, Proposition 20". Euclid's elements. Dept. Math and Computer Science, Clark University. http://aleph0.clarku.edu/~djoyce/java/elements/bookI/propI20.html.
↑ American Mathematical Monthly, pp. 49-50, 1954.
↑ Claude Irwin Palmer (1919). Practical mathematics for home study: being the essentials of arithmetic, geometry, algebra and trigonometry. McGraw-Hill. p. 422. https://archive.org/details/practicalmathema00palmiala.
↑ Alexander Zawaira; Gavin Hitchcock (2009). "Lemma 1: In a right-angled triangle the hypotenuse is greater than either of the other two sides". A primer for mathematics competitions. Oxford University Press. ISBN 978-0-19-953988-8. https://books.google.com/books?id=A21T73sqZ3AC&pg=PA30.
↑ Wolfram|Alpha. "input: solve 0<a<2a+3d, 0<a+d<2a+2d, 0<a+2d<2a+d,". Wolfram Research. http://www.wolframalpha.com/input/?i=solve%200%3Ca%3C2a%2B3d%2C%200%3Ca%2Bd%3C2a%2B2d%2C%200%3Ca%2B2d%3C2a%2Bd&t=ff3tb01. Retrieved 2010-09-07.
↑ Wolfram|Alpha. "input: solve 0<a<ar+ar², 0<ar<a+ar², 0<ar²<a+ar". Wolfram Research. http://wolframalpha.com/input?i=solve+0%3Ca%3Car%2Bar^2%2C+0%3Car%3Ca%2Bar^2%2C+0%3Car^2%3Ca%2Bar. Retrieved 2010-09-07.
↑ Wolfram|Alpha. "input: solve 0<a<ar+ar²+ar³, 0<ar³<a+ar+ar²". Wolfram Research. http://www.wolframalpha.com/input/?i=solve%20{0%3Ca%3Ca*r%2Ba*r^2%2Ba*r^3%2C%200%3Ca*r^3%3Ca%2Ba*r%2Ba*r^2}&t=ff3tb01. Retrieved 2012-07-29.
↑ John Stillwell (1997). Numbers and Geometry. Springer. ISBN 978-0-387-98289-2. https://books.google.com/books?id=4elkHwVS0eUC&pg=PA95. p. 95.
↑ Rainer Kress (1988). "§3.1: Normed spaces". Numerical analysis. Springer. p. 26. ISBN 0-387-98408-9. https://books.google.com/books?id=e7ZmHRIxum0C&pg=PA26.
↑ James Stewart (2008). Essential Calculus. Thomson Brooks/Cole. p. A10. ISBN 978-0-495-10860-3. https://archive.org/details/studentsolutions0000stew.
↑ John Stillwell (2005). The four pillars of geometry. Springer. p. 80. ISBN 0-387-25530-3. https://archive.org/details/fourpillarsofgeo0000stil.
↑ Karen Saxe (2002). Beginning functional analysis. Springer. p. 61. ISBN 0-387-95224-1. https://books.google.com/books?id=0LeWJ74j8GQC&pg=PA61.
↑ Anonymous (1854). "Exercise I. to proposition XIX". The popular educator; fourth volume. Ludgate Hill, London: John Cassell. p. 196. https://books.google.com/books?id=lTACAAAAQAAJ&pg=PA196.

References

Pedoe, Daniel (1988). Geometry: A comprehensive course. Dover. ISBN 0-486-65812-0. .
Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. ISBN 0-07-054235-X. .

External links

Triangle inequality at ProofWiki

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Triangle inequality. Read more

[1] Wolfram MathWorld – http://mathworld.wolfram.com/TriangleInequality.html

[Khamsi-2] Mohamed A. Khamsi; William A. Kirk (2001). "§1.4 The triangle inequality in $R n$ ". An introduction to metric spaces and fixed point theory. Wiley-IEEE. ISBN 0-471-41825-0. https://books.google.com/books?id=4qXbEpAK5eUC&pg=PA8.

[3] r instance, Jacobs, Harold R. (1974), Geometry, W. H. Freeman & Co., p. 246, ISBN 0-7167-0456-0

[Ramos-4] Oliver Brock; Jeff Trinkle; Fabio Ramos (2009). Robotics: Science and Systems IV. MIT Press. p. 195. ISBN 978-0-262-51309-8. https://books.google.com/books?id=fvCaQfBQ7qEC&pg=PA195.

[Ramsay-5] Arlan Ramsay; Robert D. Richtmyer (1995). Introduction to hyperbolic geometry. Springer. p. 17. ISBN 0-387-94339-0. https://archive.org/details/introductiontohy0000rams.

[Jacobs-6] Harold R. Jacobs (2003). Geometry: seeing, doing, understanding (3rd ed.). Macmillan. p. 201. ISBN 0-7167-4361-2. https://books.google.com/books?id=XhQRgZRDDq0C&pg=PA201.

[Joyce-7] David E. Joyce (1997). "Euclid's elements, Book 1, Proposition 20". Euclid's elements. Dept. Math and Computer Science, Clark University. http://aleph0.clarku.edu/~djoyce/java/elements/bookI/propI20.html.

[8] American Mathematical Monthly, pp. 49-50, 1954.

[Palmer-9] Claude Irwin Palmer (1919). Practical mathematics for home study: being the essentials of arithmetic, geometry, algebra and trigonometry. McGraw-Hill. p. 422. https://archive.org/details/practicalmathema00palmiala.

[Zawaira-10] Alexander Zawaira; Gavin Hitchcock (2009). "Lemma 1: In a right-angled triangle the hypotenuse is greater than either of the other two sides". A primer for mathematics competitions. Oxford University Press. ISBN 978-0-19-953988-8. https://books.google.com/books?id=A21T73sqZ3AC&pg=PA30.

[11] Wolfram|Alpha. "input: solve 0<a<2a+3d, 0<a+d<2a+2d, 0<a+2d<2a+d,". Wolfram Research. http://www.wolframalpha.com/input/?i=solve%200%3Ca%3C2a%2B3d%2C%200%3Ca%2Bd%3C2a%2B2d%2C%200%3Ca%2B2d%3C2a%2Bd&t=ff3tb01. Retrieved 2010-09-07.

[12] Wolfram|Alpha. "input: solve 0<a<ar+ar², 0<ar<a+ar², 0<ar²<a+ar". Wolfram Research. http://wolframalpha.com/input?i=solve+0%3Ca%3Car%2Bar^2%2C+0%3Car%3Ca%2Bar^2%2C+0%3Car^2%3Ca%2Bar. Retrieved 2010-09-07.

[13] Wolfram|Alpha. "input: solve 0<a<ar+ar²+ar³, 0<ar³<a+ar+ar²". Wolfram Research. http://www.wolframalpha.com/input/?i=solve%20{0%3Ca%3Ca*r%2Ba*r^2%2Ba*r^3%2C%200%3Ca*r^3%3Ca%2Ba*r%2Ba*r^2}&t=ff3tb01. Retrieved 2012-07-29.

[14] John Stillwell (1997). Numbers and Geometry. Springer. ISBN 978-0-387-98289-2. https://books.google.com/books?id=4elkHwVS0eUC&pg=PA95. p. 95.

[Kress-15] Rainer Kress (1988). "§3.1: Normed spaces". Numerical analysis. Springer. p. 26. ISBN 0-387-98408-9. https://books.google.com/books?id=e7ZmHRIxum0C&pg=PA26.

[Stewart-16] James Stewart (2008). Essential Calculus. Thomson Brooks/Cole. p. A10. ISBN 978-0-495-10860-3. https://archive.org/details/studentsolutions0000stew.

[Stillwell-17] John Stillwell (2005). The four pillars of geometry. Springer. p. 80. ISBN 0-387-25530-3. https://archive.org/details/fourpillarsofgeo0000stil.

[Saxe-18] Karen Saxe (2002). Beginning functional analysis. Springer. p. 61. ISBN 0-387-95224-1. https://books.google.com/books?id=0LeWJ74j8GQC&pg=PA61.

[inequality-19] Anonymous (1854). "Exercise I. to proposition XIX". The popular educator; fourth volume. Ludgate Hill, London: John Cassell. p. 196. https://books.google.com/books?id=lTACAAAAQAAJ&pg=PA196.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[math]\displaystyle{ \\|x + y\\|^2 }[/math]	[math]\displaystyle{ = \langle x + y, x + y \rangle }[/math]
	[math]\displaystyle{ = \\|x\\|^2 + \langle x, y \rangle + \langle y, x \rangle + \\|y\\|^2 }[/math]
	[math]\displaystyle{ \le \\|x\\|^2 + 2\|\langle x, y \rangle\| + \\|y\\|^2 }[/math]
	[math]\displaystyle{ \le \\|x\\|^2 + 2\\|x\\|\\|y\\| + \\|y\\|^2 }[/math] (by the Cauchy–Schwarz inequality)
	[math]\displaystyle{ = \left(\\|x\\| + \\|y\\|\right)^2 }[/math].

Anonymous

Search

Triangle inequality

Namespaces

More

Page actions

Contents

Euclidean geometry

Mathematical expression of the constraint on the sides of a triangle

Right triangle

Examples of use

Generalization to any polygon

Example of the generalized polygon inequality for a quadrilateral

Relationship with shortest paths

Converse

Generalization to higher dimensions

Normed vector space

Example norms

Metric space

Reverse triangle inequality

Triangle inequality for cosine similarity

Reversal in Minkowski space

See also

Notes

References

External links

Navigation

Navigation

Help

Translate

Wiki tools

Wiki tools

Anonymous

Search

Triangle inequality

Euclidean geometry

Mathematical expression of the constraint on the sides of a triangle

Right triangle

Examples of use

Generalization to any polygon

Example of the generalized polygon inequality for a quadrilateral

Relationship with shortest paths

Converse

Generalization to higher dimensions

Normed vector space

Example norms

Metric space

Reverse triangle inequality

Triangle inequality for cosine similarity

Reversal in Minkowski space

See also

Notes

References

External links

Navigation

Wiki tools

Page tools

Other projects

Categories