Biology:Elementary modes

Elementary modes may be considered minimal realizable flow patterns through a biochemical network that can sustain a steady state. This means that elementary modes cannot be decomposed further into simpler pathways. All possible flows through a network can be constructed from linear combinations of the elementary modes.

The set of elementary modes for a given network is unique (up to an arbitrary scaling factor). Given the fundamental nature of elementary modes in relation to uniqueness and non-decomposability, the term `pathway' can be defined as an elementary mode. Note that the set of elementary modes will change as the set of expressed enzymes change during transitions from one cell state to another. Mathematically, the set of elementary modes is defined as the set of flux vectors, [math]\displaystyle{ \mathbf{v} }[/math], that satisfy the steady state condition,

[math]\displaystyle{ \mathbf{N}\ \mathbf{v} (\mathbf{x}, \mathbf{p}) = 0 }[/math]

where [math]\displaystyle{ \mathbf{N} }[/math] is the stoichiometry matrix, [math]\displaystyle{ \mathbf{v} }[/math] is the vector of rates, [math]\displaystyle{ \mathbf{x} }[/math] the vector of steady state floating (or internal) species and [math]\displaystyle{ \mathbf{p} }[/math], the vector of system parameters.

An important condition is that the rate of each irreversible reaction must be non-negative, [math]\displaystyle{ \mathbf{v}_{irr} \geq 0 }[/math].

A more formal definition is given by:

An elementary mode, [math]\displaystyle{ \mathbf{v}_i }[/math], is defined as a vector of fluxes, [math]\displaystyle{ v_1, v_2, \ldots }[/math], such that the three conditions listed in the following criteria are satisfied.

1. The [math]\displaystyle{ \mathbf{v}_i }[/math] vector must satisfy: [math]\displaystyle{ \mathbf{N} \mathbf{v}_i = 0 }[/math], that is: the steady state condition.
2. For all irreversible reactions: [math]\displaystyle{ v_i \geq 0 }[/math]. This means that all flow patterns must use reactions that proceed in their most natural direction. This makes the pathway described by the elementary mode a thermodynamically feasible pathway.
3. The vector [math]\displaystyle{ \mathbf{v}_i }[/math] must be elementary. That is, it should not be possible to generate [math]\displaystyle{ \mathbf{v}_i }[/math] by combining two other vectors that satisfy the first and second requirements using the same set of enzymes that appear as non-zero entries in [math]\displaystyle{ \mathbf{v}_i }[/math]. In other words, it should not be possible to decompose [math]\displaystyle{ \mathbf{v}_i }[/math] into two other pathways that can themselves sustain a steady state. This is called elementarity. A more formal test is that the null space of the submatrix of [math]\displaystyle{ \mathbf{N} }[/math] that only involves the reactions of [math]\displaystyle{ \mathbf{v}_i }[/math] is of dimension one and has no zero entries.

Example

Consider a simple branched pathway with all three steps irreversible. Such a pathway will admit two elementary modes which are indicated in thicked (or red) reaction lines.

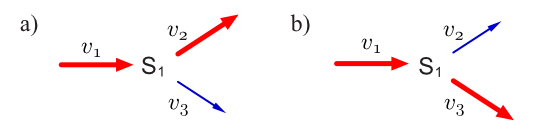
Because both [math]\displaystyle{ v_2 }[/math] and [math]\displaystyle{ v_3 }[/math] are irreversible, and elementary mode lying on both these reactions is not possible since it would mean one reactions going against its thermodynamic direction. Each mode in this system satisfies the three conditions described above. The first condition is steady state, that is for each mode [math]\displaystyle{ \mathbf{v}_i }[/math], it has to be true that [math]\displaystyle{ \mathbf{N} \mathbf{v}_i = 0 }[/math].

Algebraically the two modes are given by:

[math]\displaystyle{ \mathbf{v}_1 = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} \quad \mathbf{v}_2 = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} }[/math]

By substituting each of these vectors into [math]\displaystyle{ \mathbf{N} \mathbf{v}_i = 0 }[/math], it is easy to show that condition one is satisfied. For condition two we must ensure that all reactions that are irreversible have positive entries in the corresponding elements of the elementary modes. Since all three reactions in the branch are irreversible and all entries in the elementary modes are positive, condition two is satisfied.

Finally, to satisfy condition three, we must ask whether we can decompose the two elementary modes into other paths that can sustain a steady state while using the same non-zero entries in the elementary mode. In this example, it is impossible to decompose the elementary modes any further without disrupting the ability to sustain a steady state. Therefore, with all three conditions satisfied, we can conclude that the two vectors shown above are elementary modes.

All possible flows through a network can be constructed from linear combinations of the elementary modes, that is:

[math]\displaystyle{ \begin{align} \mathbf{v} &= \sum \lambda_i \mathbf{v}_i \\ \mbox{where}& \\ \lambda &\geq 0 \\ \end{align} }[/math]

such that the entire space of flows through a network can be described. [math]\displaystyle{ \lambda_i }[/math] must be greater than or equal to zero to ensure that irreversible steps aren't inadvertently made to go in the reverse direction. For example, the following is a possible steady-state flow in the branched pathway.

[math]\displaystyle{ v = 2.5 \begin{bmatrix} 1 \\ 1 \\ 0\end{bmatrix} + 0.5 \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 3.0 \\ 2.5 \\ 0.5 \end{bmatrix} }[/math]

If one of the outflow steps in the simple branched pathway is made reversible, an additional elementary mode becomes available, representing the flow between the two outflow branches. An additional mode emerges because, with only the first two modes, it is impossible to represent a flow between the two branches because the scaling factor, [math]\displaystyle{ \lambda_i }[/math], cannot be negative (which would be required to reverse the flow).

Definition of a Pathway

The Wikipedia page Metabolic pathway defines a pathway as "a metabolic pathway is a linked series of chemical reactions occurring within a cell". This means that any sequence of reactions can be labeled a metabolic pathway. However, as metabolism was being uncovered, groups of reactions were assigned specific labels, such as glycolysis, Krebs Cycle, or Serine biosynthesis. Often the categorization was based on common chemistry or identification of an input and output. For example, serine biosynthesis starts at 3-phosphoglycerate and ends at serine. This is a somewhat ad hoc means for defining pathways, particularly when pathways are dynamic structures, changing as environmental result in changes in gene expression. For example, the Kreb Cycle is often not cyclic as depicted in textbooks. In E. coli and other bacteria, it is only cyclic during aerobic growth on acetate or fatty acids. Instead, under anaerobiosis, its enzymes function as two distinct biosynthetic pathways producing succinyl-CoA and α-ketoglutarate.

It has therefore been proposed to define a pathway as either a single elementary mode or some combination of elementary modes. The added advantage is that the set of elementary modes is unique and non-decomposable to simpler pathways. A single elementary mode can therefore be thought of as an elementary pathway. Note that the set of elementary modes will change as the set of expressed enzymes change during transitions from one cell state to another.

Elementary modes, therefore, provide an unambiguous definition of a pathway.

Comment on Condition Three

Condition three relates to the non-decomposability of an elementary mode and is partly what makes elementary modes interesting. The two other important features as indicated before are pathway uniqueness and thermodynamic plausibility. Decomposition implies that it is possible to represent a mode as a combination of two or more other modes. For example, a mode [math]\displaystyle{ \mathbf{e}_1 }[/math] might be composed from two other modes, [math]\displaystyle{ \mathbf{e}_2 }[/math] and [math]\displaystyle{ \mathbf{e}_3 }[/math]:

[math]\displaystyle{ \mathbf{e}_1 = \lambda_1 \mathbf{e}_2 + \lambda_2 \mathbf{e}_3 }[/math]

If a mode can be decomposed, does it mean that the mode is not an elementary mode? Condition three provides a rule to determine whether a decomposition means that a given mode is an elementary mode or not. If it is only possible to decompose a given mode by introducing enzymes that are not used in the mode, then the mode is elementary. That is, is there more than one way to generate a pathway (i.e., something that can sustain a steady state) with the enzymes currently used in the mode? If so, then the mode is not elementary. To illustrate this subtle condition, consider the pathway shown in below.

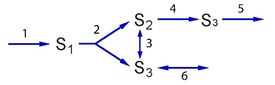
This pathway represents a stylized rendition of glycolysis. Step three and six are reversible and correspond to triose phosphate isomerase and glycerol 3-phosphate dehydrogenase, respectively.

The network has four elementary flux modes, which are shown in the figure below.

The elementary flux mode vectors are shown below:

[math]\displaystyle{ \begin{array}{l} \qquad\ \mathbf{e}_1 \quad \ \ \mathbf{e}_2 \quad \mathbf{e}_3 \quad \mathbf{e}_4 \\ \begin{bmatrix} & \phantom{-}0 & \phantom{-}1 & \phantom{-}1 & \phantom{-}1 \\ & \phantom{-}0 & \phantom{-}1 & \phantom{-}1 & \phantom{-}1 \\ & \phantom{-}1 & -1 & \phantom{-}1 & \phantom{-}0 \\ & \phantom{-}1 & \phantom{-}0 & \phantom{-}2 & \phantom{-}1 \\ & \phantom{-}1 & \phantom{-}0 & \phantom{-}2 & \phantom{-}1 \\ & -1 & \phantom{-}2 & \phantom{-}0 & \phantom{-}1 \\ \end{bmatrix} \\ \end{array} }[/math]

Note that it is possible to have negative entries in the set of elementary modes because they will correspond to the reversible steps. Of interest is the observation that the fourth vector, [math]\displaystyle{ e_4 = [ 1\ 1\ 0\ 1\ 1\ 1\ ]^T }[/math] (where [math]\displaystyle{ T }[/math] represents the transpose) can be formed from the sum of the first and second vectors. This suggests that the fourth vector is not an elementary mode.

[math]\displaystyle{ \mathbf{e}_4 \begin{bmatrix} \phantom{-}1 \phantom{-} \\ \phantom{-}1 \phantom{-} \\ \phantom{-}0 \phantom{-} \\ \phantom{-}1 \phantom{-}\\ \phantom{-}1 \phantom{-}\\ \phantom{-}1 \phantom{-}\\ \end{bmatrix} = \mathbf{e}_1 \begin{bmatrix} \phantom{-}0 \phantom{-} \\ \phantom{-}0 \phantom{-}\\ \phantom{-}1 \phantom{-}\\ \phantom{-}1 \phantom{-}\\ \phantom{-}1 \phantom{-}\\ -1 \phantom{-}\\ \end{bmatrix} + \mathbf{e}_2 \begin{bmatrix} \phantom{-}1 \phantom{-}\\ \phantom{-}1 \phantom{-}\\ -1 \phantom{-}\\ \phantom{-}0 \phantom{-}\\ \phantom{-}0 \phantom{-}\\ \phantom{-}2 \phantom{-}\\ \end{bmatrix} }[/math]

However, this decomposition only works because we have introduced a new enzyme, [math]\displaystyle{ E_4 }[/math] (triose phosphate isomerase) which is not used in [math]\displaystyle{ \mathbf{e}_4 }[/math]. It is, in fact impossible to decompose [math]\displaystyle{ \mathbf{e}_4 }[/math] into pathways that can sustain a steady state with only the five steps, [math]\displaystyle{ e_1, e_2, e_4, e_5\ \mbox{and}\ e_6 }[/math], used in the elementary mode. We conclude therefore that [math]\displaystyle{ \mathbf{e}_4 }[/math] is an elementary mode.

See also

• Computational systems biology
• Metabolic control analysis
• Metabolic network
• Metabolic pathway
• Metagenomics