Biology:Luria–Delbrück experiment

From HandWiki
The two possibilities tested by the Luria–Delbrück experiment. (A) If mutations are induced by the media, roughly the same number of mutants are expected to appear on each plate. (B) If mutations arise spontaneously during cell divisions prior to plating, each plate will have a highly variable number of mutants.

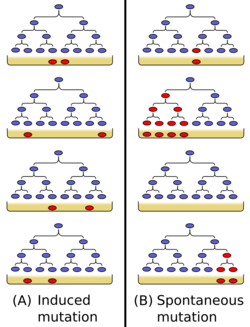
The Luria–Delbrück experiment (1943) (also called the Fluctuation Test) demonstrated that in bacteria, genetic mutations arise in the absence of selective pressure rather than being a response to it. Thus, it concluded Darwin's theory of natural selection acting on random mutations applies to bacteria as well as to more complex organisms. Max Delbrück and Salvador Luria won the 1969 Nobel Prize in Physiology or Medicine in part for this work.

History

By the 1940s the ideas of inheritance and mutation were generally accepted, though the role of DNA as the hereditary material had not yet been established. It was thought that bacteria were somehow different and could develop heritable genetic mutations depending on the circumstances they found themselves: in short, was the mutation in bacteria pre-adaptive (pre-existent) or post-adaptive (directed adaption)?[1]

In their experiment, Luria and Delbrück inoculated a small number of bacteria (Escherichia coli) into separate culture tubes. After a period of growth, they plated equal volumes of these separate cultures onto agar containing the T1 phage (virus). If resistance to the virus in bacteria were caused by an induced activation in bacteria i.e. if resistance were not due to heritable genetic components, then each plate should contain roughly the same number of resistant colonies. Assuming a constant rate of mutation, Luria hypothesized that if mutations occurred after and in response to exposure to the selective agent, the number of survivors would be distributed according to a Poisson distribution with the mean equal to the variance. This was not what Delbrück and Luria found: Instead the number of resistant colonies on each plate varied drastically: the variance was considerably greater than the mean.

Luria and Delbrück proposed that these results could be explained by the occurrence of a constant rate of random mutations in each generation of bacteria growing in the initial culture tubes. Based on these assumptions Delbrück derived a probability distribution (now called the Luria–Delbrück distribution[2][3]) that gives a relationship between moments consistent with the experimentally obtained values. Therefore, the conclusion was that mutations in bacteria, as in other organisms, are random rather than directed.[4]

The results of Luria and Delbrück were confirmed in more graphical, but less quantitative, way by Newcombe. Newcombe incubated bacteria in a Petri dish for a few hours, then replica plated it onto two new Petri dishes treated with phage. The first plate was left unspread, and the second plate was then respread, that is, bacterial cells were moved around allowing single cells in some colony to form their own new colonies. If colonies contained resistant bacterial cells before entering into contact with the phage virus, one would expect that some of these cells would form new resistant colonies on the respread dish and so to find a higher number of surviving bacteria there. When both plates were incubated for growth, there were actually as much as 50 times greater number of bacterial colonies on the respread dish. This showed that bacterial mutations to virus resistance had randomly occurred during the first incubation. Once again, the mutations occurred before selection was applied.[5]

More recently, the results of Luria and Delbrück were questioned by Cairns and others, who studied mutations in sugar metabolism as a form of environmental stress.[6] Some scientists suggest that this result may have been caused by selection for gene amplification and/or a higher mutation rate in cells unable to divide.[7] Others have defended the research and propose mechanisms which account for the observed phenomena consistent with adaptive mutagenesis.[8]

This distribution appears to have been first determined by Haldane.[9] An unpublished manuscript was discovered in 1991 at University College London describing this distribution. The derivation is different but the results are difficult to compute without the use of a computer.

Description of the test

A small number of cells are used to inoculate parallel cultures in a non-selective medium.[10] The cultures are grown to saturation to obtain equal cell densities. The cells are plated onto selective media to obtain the number of mutants (r). Dilutions are plated onto rich medium to calculate the total number of viable cells ( Nt ). The number of mutants that appear in the saturated culture is a measure of both the mutation rate and when the mutants arise during the growth of the culture: mutants appearing early in the growth of the culture will propagate many more mutants than those that arise later during growth. These factors cause the frequency ( r / Nt ) to vary greatly, even if the number of mutational events ( m ) is the same. Frequency is not a sufficiently accurate measure of mutation and the mutation rate (m / Nt) should always be calculated.

The estimation of the mutation rate (μ) is complex. Luria and Delbruck estimated this parameter from the mean of the distribution but this estimator was subsequently shown to be biased.

The Lea-Coulson method of the median was introduced in 1949.[11] This method is based on the equation

[math]\displaystyle{ \frac{ r }{ m } - \ln( m ) - 1.24 = 0 . }[/math]
Where:
r = median number of colonies on one plate containing the indicator (e.g. rifampicin, sodium chlorate, streptomycin)
m = a variable which will be varied, corresponds to the mutations/culture
The value of the variable m is adjusted until the total value of the equation is close to 0. Then the mutation rate (probablitity of a mutation/cell/division or generation) can be calculated as one of three formulae:
(1) [math]\displaystyle{ \mu = m/median(N_t) }[/math]
(2) [math]\displaystyle{ \mu = m/(2*median(N_t)) }[/math]
(3) [math]\displaystyle{ \mu = m*ln(2)/median(N_t) }[/math]
where Nt is the median of the number of viable cells on a non-indicator plate (often LB agar with no additive)
The choice of which formula to use depends on at which stage in the cell division that the mutations are expected to occur. [12]

This method has since been improved on but these more accurate methods are complex. The Ma-Sandri-Sarkar maximum likelihood estimator is currently the best known estimator.[13] A number of additional methods and estimates from experimental data have been described.[14]

Two web-applications for the calculation of the mutation rate are freely available: Falcor [10] and bz-rates. Bz-rates implements a generalized version of the Ma-Sandri-Sarkar maximum likelihood estimator that can take into account the relative differential growth rate between mutant and wild-type cells as well as a generating function estimator that can estimate both the mutation rate and the differential growth rate. A worked example is shown in this paper by Jones et al.[15]

Distribution

In all these models the mutation rate (μ) and growth rate (β) were assumed to be constant. The model can be easily generalized to relax these and other constraints.[16] These rates are likely to differ in non experimental settings. The models also require that Nt μ >> 1 where Nt is the total number of organisms. This assumption is likely to hold in most realistic or experimental settings.

Luria and Delbrück[4] estimated the mutation rate (mutations per bacterium per unit time) from the equation

[math]\displaystyle{ \mu = \frac{ \beta \ln( \rho ) }{ n_0[1 - \exp(\beta t )] } }[/math]

where β is the cellular growth rate, n0 is the initial number of bacteria in each culture, t is the time, and

[math]\displaystyle{ \rho = \frac{ N_s } N }[/math]

where Ns is the number of cultures without resistant bacteria and N is the total number of cultures.

Lea and Coulson's model[11] differed from the original in that they considered a collection of independent Yule processes (a filtered Poisson process). Numerical comparisons of these two models with realistic values of the parameters has shown that they differ only slightly.[17] The generating function for this model was found by Bartlett in 1978[18] and is

[math]\displaystyle{ G( z, \mu, \phi) = \exp\left( \frac{ \mu }{ \phi }\left( \frac{ 1 }{ z } - 1 \right) \log\left( 1 - \phi z \right) \right) }[/math]

where μ is the mutation rate (assumed to be constant), φ = 1 − e−βt with β as the cellular growth rate (also assumed to be constant) and t as the time.

The determination of μ from this equation has proved difficult but a solution was discovered in 2005[citation needed]. Differentiation of the generating function with respect to μ allows the application of the Newton–Raphson method which together with the use of a score function allows one to obtain confidence intervals for μ.

Molecular biology

The mechanism of resistance to the phage T1 appears to have been due to mutations in the fhuA gene - a membrane protein that acts as the T1 receptor.[19] The tonB gene product is also required for infection by T1. The FhuA protein is actively involved in the transport of ferrichrome, albomycin and rifamycin.[20] It also confers sensitivity to microcin J25 and colicin M and acts as a receptor for the phages T5 and phi80 as well as T1.

The FhuA protein has a beta-barrel domain (residues 161 to 714) that is closed by a globular cork domain (residues 1 to 160).[21] Within the cork domain is the TonB binding region (residues 7 to 11). The large membrane spanning monomeric β-barrel domains have 22 β-strands of variable length, several of which extend significantly beyond the membrane hydrophobic core into the extracellular space. There are 11 extracellular loops numbered L1 to L11. The L4 loop is where the T1 phage binds.

References

  1. ↑ Luria SE (1984) A slot machine, a broken test tube: An autobiography. Harper & Row
  2. ↑ Zheng, Q. (1999). "Progress of a half century in the study of the Luria–Delbrück distribution". Mathematical Biosciences 162 (1–2): 1–32. doi:10.1016/S0025-5564(99)00045-0. PMID 10616278. https://zenodo.org/record/1259661. 
  3. ↑ Zheng, Q. (2010). "The Luria-Delbrück distribution: early statistical thinking about evolution". Chance 23: 15–18. doi:10.1007/s00144-010-0017-y. 
  4. ↑ 4.0 4.1 Luria, S. E.; Delbrück, M. (1943). "Mutations of Bacteria from Virus Sensitivity to Virus Resistance". Genetics 28 (6): 491–511. doi:10.1093/genetics/28.6.491. PMID 17247100. PMC 1209226. http://www.genetics.org/cgi/reprint/28/6/491. 
  5. ↑ Newcombe, H. B. (1949). "Origin of Bacterial Variants". Nature 164 (4160): 150–151. doi:10.1038/164150a0. PMID 18146850. Bibcode: 1949Natur.164..150N. 
  6. ↑ Cairns, J.; Overbaugh, J.; Miller, S. (1988). "The Origin of Mutants". Nature 335 (6186): 142–145. doi:10.1038/335142a0. PMID 3045565. Bibcode: 1988Natur.335..142C. 
  7. ↑ Slechta, E. S.; Liu, J.; Andersson, D. I.; Roth, J. R. (2002). "Evidence that selected amplification of a bacterial lac frameshift allele stimulates Lac(+) reversion (adaptive mutation) with or without general hypermutability". Genetics 161 (3): 945–956. doi:10.1093/genetics/161.3.945. PMID 12136002. PMC 1462195. http://www.genetics.org/cgi/content/full/161/3/945. 
  8. ↑ Foster, Patricia L. (2004). "Adaptive Mutation in Escherichia coli". Journal of Bacteriology 186 (15): 4846–4852. doi:10.1128/jb.186.15.4846-4852.2004. PMID 15262917. 
  9. ↑ Sarkar, S (1991). "Haldane's solution of the Luria-Delbruck distribution". Genetics 127 (2): 257–261. doi:10.1093/genetics/127.2.257. PMID 2004702. 
  10. ↑ 10.0 10.1 Hall, BM; Ma, CX; Liang, P; Singh, KK (2009). "Fluctuation analysis CalculatOR: a web tool for the determination of mutation rate using Luria-Delbruck fluctuation analysis". Bioinformatics 25 (12): 1564–1565. doi:10.1093/bioinformatics/btp253. PMID 19369502. 
  11. ↑ 11.0 11.1 Lea, DE; Coulson, CA (1949). "The distribution of the numbers of mutants in bacterial populations". J Genet 49 (3): 264–285. doi:10.1007/bf02986080. PMID 24536673. 
  12. ↑ Foster, Patricia L. (2006), "Methods for Determining Spontaneous Mutation Rates" (in en), DNA Repair, Part B, Methods in Enzymology, 409, Elsevier, pp. 195–213, doi:10.1016/s0076-6879(05)09012-9, ISBN 978-0-12-182814-1, PMID 16793403 
  13. ↑ Zheng, Q (2000). "Statistical and algorithmic methods for fluctuation analysis with SALVADOR as an implementation". Math Biosci 176 (2): 237–252. doi:10.1016/S0025-5564(02)00087-1. PMID 11916511. 
  14. ↑ Rosche, WA; Foster, PL (2000). "Determining mutation rates in bacterial populations". Methods 20 (1): 4–17. doi:10.1006/meth.1999.0901. PMID 10610800. 
  15. ↑ Jones, ME; Thomas, SM; Rogers, A (1994). "Luria-Delbruk experiments: Design and analysis". Genetics 136: 1209–1216. doi:10.1093/genetics/136.3.1209. 
  16. ↑ Houchmandzadeh, B. (2015). "General formulation of Luria-Delbrück distribution of the number of mutants". Phys. Rev. E 92 (1): 012719. doi:10.1103/PhysRevE.92.012719. PMID 26274214. Bibcode: 2015PhRvE..92a2719H. https://hal.archives-ouvertes.fr/hal-01148693v2/document. 
  17. ↑ Zheng, Q (1999). "Progress of a half century in the study of the Luria–Delbrück distribution". Mathematical Biosciences 162 (1–2): 1–32. doi:10.1016/s0025-5564(99)00045-0. PMID 10616278. https://zenodo.org/record/1259661. 
  18. ↑ Bartlett M. (1978) An introduction to stochastic processes. Cambridge University Press, Cambridge, 3rd edition
  19. ↑ Carvajal-Rodríguez, A. (2012). "Teaching the fluctuation test in silico by using mutate: A program to distinguish between the adaptive and spontaneous mutation hypotheses". Biochemistry and Molecular Biology Education 40 (4): 277–283. doi:10.1002/bmb.20615. PMID 22807434. 
  20. ↑ Endriss, F; Braun, M; Killmann, H; Braun, V (2003). "Mutant analysis of the Escherichia coli FhuA protein reveals sites of FhuA activity". J Bacteriol 185 (16): 4683–4692. doi:10.1128/jb.185.16.4683-4692.2003. PMID 12896986. 
  21. ↑ Killmann, H; Braun, M; Herrmann, C; Braun, V (2001). "FhuA barrel-cork hybrids are active transporters and receptors". J Bacteriol 183 (11): 3476–3487. doi:10.1128/jb.183.11.3476-3487.2001. PMID 11344156. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Biology:Luria–Delbrück_experiment&oldid=3575448"