Bird–Meertens formalism
The Bird–Meertens formalism (BMF) is a calculus for deriving programs from program specifications (in a functional programming setting) by a process of equational reasoning. It was devised by Richard Bird and Lambert Meertens as part of their work within IFIP Working Group 2.1.
It is sometimes referred to in publications as BMF, as a nod to Backus–Naur form. Facetiously it is also referred to as Squiggol, as a nod to ALGOL, which was also in the remit of WG 2.1, and because of the "squiggly" symbols it uses. A less-used variant name, but actually the first one suggested, is SQUIGOL. Martin and Nipkow provided automated support for Squiggol development proofs, using the Larch Prover.[1]
Basic examples and notations
Map is a well-known second-order function that applies a given function to every element of a list; in BMF, it is written [math]\displaystyle{ * }[/math]:
- [math]\displaystyle{ f*[e_1,\dots,e_n] = [f\ e_1,\dots,f\ e_n]. }[/math]
Likewise, reduce is a function that collapses a list into a single value by repeated application of a binary operator. It is written / in BMF. Taking [math]\displaystyle{ \oplus }[/math] as a suitable binary operator with neutral element e, we have
- [math]\displaystyle{ \oplus / [e_1,\dots,e_n] = e \oplus e_1 \oplus \dots \oplus e_n. }[/math]
Using those two operators and the primitives [math]\displaystyle{ + }[/math] (as the usual addition), and [math]\displaystyle{ +\!\!\!+ }[/math] (for list concatenation), we can easily express the sum of all elements of a list, and the flatten function, as [math]\displaystyle{ {\rm sum} = + / }[/math] and [math]\displaystyle{ {\rm flatten} = +\!\!\!+ / }[/math], in point-free style. We have:
- [math]\displaystyle{ {\rm sum}\ [e_1,\dots,e_n] = + / [e_1,\dots,e_n] = 0 + e_1 + \dots+ e_n = \sum_k e_k. }[/math]
- [math]\displaystyle{ {\rm flatten}\ [l_1,\dots,l_n] =+\!\!\!+ / [l_1,\dots,l_n] = [\,] +\!\!\!+\; l_1 +\!\!\!+ \dots+\!\!\!+\; l_n = \text{ the concatenation of all lists } l_k. }[/math]
Similarly, writing [math]\displaystyle{ \cdot }[/math] for functional composition and [math]\displaystyle{ \land }[/math] for conjunction, it is easy to write a function testing that all elements of a list satisfy a predicate p, simply as [math]\displaystyle{ {\rm all}\ p = (\land /)\cdot(p*) }[/math]:
- [math]\displaystyle{ \begin{align} {\rm all}\ p\ [e_1,\dots,e_n] &= (\land /)\cdot(p*)\ [e_1,\dots,e_n] \\&= \land /(p* [e_1,\dots,e_n]) \\&= \land /[p\ e_1,\dots,p\ e_n] \\&= p\ e_1\land \dots \land p\ e_n \\&= \forall k\ . \ p\ e_k. \end{align} }[/math]
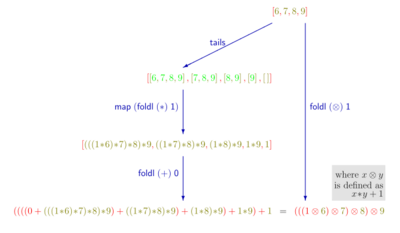
Bird (1989) transforms inefficient easy-to-understand expressions ("specifications") into efficient involved expressions ("programs") by algebraic manipulation. For example, the specification "[math]\displaystyle{ \mathrm{max} \cdot \mathrm{map} \; \mathrm{sum} \cdot \mathrm{segs} }[/math]" is an almost literal translation of the maximum segment sum problem,[6] but running that functional program on a list of size [math]\displaystyle{ n }[/math] will take time [math]\displaystyle{ \mathcal{O}(n^3) }[/math] in general. From this, Bird computes an equivalent functional program that runs in time [math]\displaystyle{ \mathcal{O}(n) }[/math], and is in fact a functional version of Kadane's algorithm.
The derivation is shown in the picture, with computational complexities[7] given in blue, and law applications indicated in red. Example instances of the laws can be opened by clicking on [show]; they use lists of integer numbers, addition, minus, and multiplication. The notation in Bird's paper differs from that used above: [math]\displaystyle{ \mathrm{map} }[/math], [math]\displaystyle{ \mathrm{concat} }[/math], and [math]\displaystyle{ \mathrm{foldl} }[/math] correspond to [math]\displaystyle{ * }[/math], [math]\displaystyle{ \mathrm{flatten} }[/math], and a generalized version of [math]\displaystyle{ / }[/math] above, respectively, while [math]\displaystyle{ \mathrm{inits} }[/math] and [math]\displaystyle{ \mathrm{tails} }[/math] compute a list of all prefixes and suffixes of its arguments, respectively. As above, function composition is denoted by "[math]\displaystyle{ \cdot }[/math]", which has lowest binding precedence. In the example instances, lists are colored by nesting depth; in some cases, new operations are defined ad hoc (grey boxes).
The homomorphism lemma and its applications to parallel implementations
A function h on lists is called a list homomorphism if there exists an associative binary operator [math]\displaystyle{ \oplus }[/math] and neutral element [math]\displaystyle{ e }[/math] such that the following holds:
- [math]\displaystyle{ \begin{align} &h\ [\,] &&=\ e \\ &h\ (l +\!\!\!+\; m) &&=\ h\ l \oplus h\ m. \end{align} }[/math]
The homomorphism lemma states that h is a homomorphism if and only if there exists an operator [math]\displaystyle{ \oplus }[/math] and a function f such that [math]\displaystyle{ h = (\oplus/)\cdot(f*) }[/math].
A point of great interest for this lemma is its application to the derivation of highly parallel implementations of computations. Indeed, it is trivial to see that [math]\displaystyle{ f* }[/math] has a highly parallel implementation, and so does [math]\displaystyle{ \oplus/ }[/math] — most obviously as a binary tree. Thus for any list homomorphism h, there exists a parallel implementation. That implementation cuts the list into chunks, which are assigned to different computers; each computes the result on its own chunk. It is those results that transit on the network and are finally combined into one. In any application where the list is enormous and the result is a very simple type – say an integer – the benefits of parallelisation are considerable. This is the basis of the map-reduce approach.
See also
- Catamorphism
- Anamorphism
- Paramorphism
- Hylomorphism
References
- ↑ Ursula Martin; Tobias Nipkow (Apr 1990). "Proc. IFIP WG 2.2/2.3 Working Conference on Programming Concepts and Methods". North-Holland. pp. 233–247.
- ↑ Bird 1989, Sect.8, p.126r.
- ↑ 3.0 3.1 Bird 1989, Sect.2, p.123l.
- ↑ Bird 1989, Sect.7, Lem.1, p.125l.
- ↑ 5.0 5.1 Bird 1989, Sect.5, p.124r.
- ↑ Where [math]\displaystyle{ \mathrm{max} }[/math], [math]\displaystyle{ \mathrm{sum} }[/math], and [math]\displaystyle{ \mathrm{segs} }[/math] returns the largest value, the sum, and the list of all segments (i.e. sublists) of a given list, respectively.
- ↑ Each expression in a line denotes an executable functional program to compute the maximum segment sum.
- de Bakker, J.W.; Hazewinkel, M.; Lenstra, J.K., eds (1986). "Algorithmics: Towards programming as a mathematical activity". Mathematics and Computer Science. CWI Monographs. 1. North-Holland. pp. 289–334. https://ir.cwi.nl/pub/2686.
- "Two Exercises Found in a Book on Algorithmics". North-Holland. 1987. https://www.kestrel.edu/people/meertens/publications/papers/Two_exercises_found_in_a_book_on_Algorithmics.pdf.
- Template:Cite tech report
- "Algebraic Identities for Program Calculation". The Computer Journal 32 (2): 122–126. 1989. doi:10.1093/comjnl/32.2.122. https://academic.oup.com/comjnl/article-pdf/32/2/122/1445670/320122.pdf.
- Cole, Murray (1993). "Parallel Programming, List Homomorphisms and the Maximum Segment Sum Problem". pp. 489–492. http://homepages.inf.ed.ac.uk/mic/Pubs/segmentsum.ps.gz.
- "Elements of a Relational Theory of Datatypes". 1993. pp. 7-42. doi:10.1007/3-540-57499-9_15. ISBN 978-3-540-57499-6. https://www.researchgate.net/profile/Roland-Backhouse/publication/221509704_Elements_of_a_Relational_Theory_of_Datatypes/links/00b7d52caa66af36d1000000/Elements-of-a-Relational-Theory-of-Datatypes.pdf.
- Bunkenburg, Alexander (1994). "The Boom Hierarchy". in O'Donnell, John T.; Hammond, Kevin (PDF). London: Springer. 1–8. doi:10.1007/978-1-4471-3236-3_1. ISBN 978-1-4471-3236-3. https://citeseerx.ist.psu.edu/pdf/dd3ed1c7d523781513f01d25e1be472de4279d72.
- Algebra of Programming. International Series in Computing Science. 100. Prentice Hall. 1997. ISBN 0-13-507245-X.
- Troy Astarte, ed (2020). "The School of Squiggol: A History of the Bird-Meertens Formalism". 12233. Springer. doi:10.1007/978-3-030-54997-8_2. http://www.cs.ox.ac.uk/people/jeremy.gibbons/publications/squiggol-history.pdf.
 |