Blossom tree (graph theory)
In the study of planar graphs, blossom trees are trees with additional directed half edges. Each blossom tree is associated with an embedding of a planar graph. Blossom trees can be used to sample random planar graphs.[1]
Description
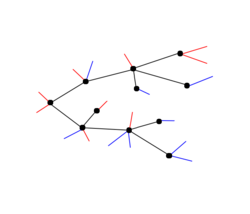
A blossom tree is constructed from a rooted tree embedded in the plane by adding opening and closing stems to vertices. The number of opening and closing stems must match.[2] Some authors require that blossom trees be rooted and put conditions on which kind of stems they can carry.[3] The terms leaves and blossoms are also sometimes used for opening and closing stems.[3][4]
Relationship with planar graphs
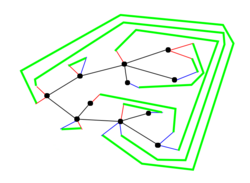
An embedded planar graph can be built from a blossom tree by connecting each opening stem to a closing stem. One visits the half-edges by going around the graph clockwise starting at an opening stem. If the tree is rooted, one usually starts at the root. The algorithm is analogous to parenthesis matching and uses a stack. At each stage, if the type of the current half-edge is the same as the half edge at the top of the stack, is pushed onto the stack. If the colors differ, the stack is popped and the two half-edges are connected.[4] If we orient the added edges from opening to closing stem, we have no counter-clockwised edges. This process takes linear time.[1]
Similarly, an embedding of a rooted planar graph can be encoded as a blossom tree. If the root is in the corner, this can be done in linear time. The edges of a rooted planar graph can be oriented so that there is a path from the root to any vertex, but there are no counter-clockwise cycles. In this case, one can use a depth-first algorithm to turn it into a blossom tree. Starting with the root vertex, look at every edge incident to it. If it points away from our current vertex, cut it, labelling the outward half-edge as a closing stem and inward half-edge as an opening stem. If it points toward our current vertex, mark it as to be kept and set its other endpoint as our current vertex. Continue until all edges have been considered. If the map is not rooted in a corner, constructing the blossom tree takes quadratic time.[1]
Use in knot theory
Blossom trees are also used to randomly generate large knot diagrams. Knots can be represented by 4-regular planar graphs where each node is marked as an overcrossing or undercrossings. Blossom trees can be used to generate random 4-regular planar graphs. However, these do not always give knot diagrams as there may be more than one component. This can be checked in cubic time.[5]
References
- ↑ 1.0 1.1 1.2 Albenque, Marie; Poulalhon, Dominique (2015). "Generic method for bijections between blossoming trees and planar maps". arXiv:1305.1312v3 [math.CO].
- ↑ Albenque, Marie. "Blossoming trees and planar maps". http://www.lix.polytechnique.fr/~albenque/slides/Albenque_IHP.pdf. Retrieved 21 December 2015.
- ↑ 3.0 3.1 Calvo, Jorge Alberto (2005-01-01) (in en). Physical and Numerical Models in Knot Theory: Including Applications to the Life Sciences. World Scientific. ISBN 9789812703460. https://books.google.com/books?id=ZN-QYNl3ZtwC&dq=blossom%2520tree%2520regular%2520planar%2520graph&pg=PA480.
- ↑ 4.0 4.1 Schaeffer, Gilles; Denise, Alain. "Conjugation of trees and random maps". http://algo.inria.fr/seminars/sem98-99/schaeffer.pdf. Retrieved 21 December 2015.
- ↑ Calvo, Jorge A.; Millett, Kenneth C.; Rawdon, Eric J.; Stasiak, Andrzej (2005-09-20) (in en). Physical and Numerical Models in Knot Theory: Including Applications to the Life Sciences. World Scientific. ISBN 9789814480857. https://books.google.com/books?id=D-fICgAAQBAJ&dq=blossom%2520tree&pg=PA479.
 |
