Stack (abstract data type)

From HandWiki
Short description: Abstract data type

Similarly to a stack of plates, adding or removing is only possible at the top.
Simple representation of a stack runtime with push and pop operations.

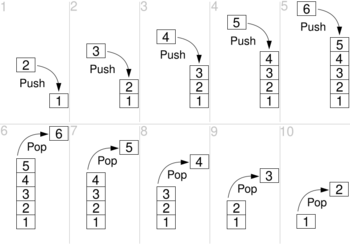
In computer science, a stack is an abstract data type that serves as a collection of elements with two main operations:

  • Push, which adds an element to the collection, and
  • Pop, which removes the most recently added element.

Additionally, a peek operation can, without modifying the stack, return the value of the last element added. The name stack is an analogy to a set of physical items stacked one atop another, such as a stack of plates.

The order in which an element added to or removed from a stack is described as last in, first out, referred to by the acronym LIFO.[nb 1] As with a stack of physical objects, this structure makes it easy to take an item off the top of the stack, but accessing a datum deeper in the stack may require removing multiple other items first.[1]

Considered a linear data structure, or more abstractly a sequential collection, a stack has one end which is the only position at which the push and pop operations may occur, the top of the stack, and is fixed at the other end, the bottom. This data structure makes it possible to implement a stack as a singly linked list and as a pointer to the top element. A stack may be implemented to have a bounded capacity. If the stack is full and does not contain enough space to accept another element, the stack is in a state of stack overflow.

A stack is needed to implement depth-first search.

History

Stacks entered the computer science literature in 1946, when Alan Turing used the terms "bury" and "unbury" as a means of calling and returning from subroutines.[2][3] Subroutines and a two-level stack had already been implemented in Konrad Zuse's Z4 in 1945.[4][5]

Klaus Samelson and Friedrich L. Bauer of Technical University Munich proposed the idea of a stack called Operationskeller ("operational cellar") in 1955[6][7] and filed a patent in 1957.[8][9][10][11] In March 1988, by which time Samelson was deceased, Bauer received the IEEE Computer Pioneer Award for the invention of the stack principle.[12][7] Similar concepts were independently developed by Charles Leonard Hamblin in the first half of 1954[13][7] and by Wilhelm Kämmerer (de) with his automatisches Gedächtnis ("automatic memory") in 1958.[14][15][7]

Stacks are often described using the analogy of a spring-loaded stack of plates in a cafeteria.[16][1][17] Clean plates are placed on top of the stack, pushing down any plates already there. When the top plate is removed from the stack, the one below it is elevated to become the new top plate.

Non-essential operations

In many implementations, a stack has more operations than the essential "push" and "pop" operations. An example of a non-essential operation is "top of stack", or "peek", which observes the top element without removing it from the stack.[18] Since this can be broken down into a "pop" followed by a "push" to return the same data to the stack, it is not considered an essential operation. If the stack is empty, an underflow condition will occur upon execution of either the "stack top" or "pop" operations. Additionally, many implementations provide a check if the stack is empty and an operation that returns its size.

Software stacks

Implementation

A stack can be easily implemented either through an array or a linked list, as it is merely a special case of a list. In either case, what identifies the data structure as a stack is not the implementation but the interface: the user is only allowed to pop or push items onto the array or linked list, with few other helper operations. The following will demonstrate both implementations using pseudocode.

Array

An array can be used to implement a (bounded) stack, as follows. The first element, usually at the zero offset, is the bottom, resulting in array[0] being the first element pushed onto the stack and the last element popped off. The program must keep track of the size (length) of the stack, using a variable top that records the number of items pushed so far, therefore pointing to the place in the array where the next element is to be inserted (assuming a zero-based index convention). Thus, the stack itself can be effectively implemented as a three-element structure: 

structure stack:
    maxsize : integer
    top : integer
    items : array of item

procedure initialize(stk : stack, size : integer):
    stk.items ← new array of size items, initially empty
    stk.maxsize ← size
    stk.top ← 0

The push operation adds an element and increments the top index, after checking for overflow: 

procedure push(stk : stack, x : item):
    if stk.top = stk.maxsize:
        report overflow error
    else:
        stk.items[stk.top] ← x
        stk.top ← stk.top + 1

Similarly, pop decrements the top index after checking for underflow, and returns the item that was previously the top one: 

procedure pop(stk : stack):
    if stk.top = 0:
        report underflow error
    else:
        stk.top ← stk.top − 1
        r ← stk.items[stk.top]
        return r

Using a dynamic array, it is possible to implement a stack that can grow or shrink as much as needed. The size of the stack is simply the size of the dynamic array, which is a very efficient implementation of a stack since adding items to or removing items from the end of a dynamic array requires amortized O(1) time.

Linked list

Another option for implementing stacks is to use a singly linked list. A stack is then a pointer to the "head" of the list, with perhaps a counter to keep track of the size of the list: 

structure frame:
    data : item
    next : frame or nil

structure stack:
    head : frame or nil
    size : integer

procedure initialize(stk : stack):
    stk.head ← nil
    stk.size ← 0

Pushing and popping items happens at the head of the list; overflow is not possible in this implementation (unless memory is exhausted): 

procedure push(stk : stack, x : item):
    newhead ← new frame
    newhead.data ← x
    newhead.next ← stk.head
    stk.head ← newhead
    stk.size ← stk.size + 1

procedure pop(stk : stack):
    if stk.head = nil:
        report underflow error
    r ← stk.head.data
    stk.head ← stk.head.next
    stk.size ← stk.size - 1
    return r

Stacks and programming languages

Some languages, such as Perl, LISP, JavaScript and Python, make the stack operations push and pop available on their standard list/array types. Some languages, notably those in the Forth family (including PostScript), are designed around language-defined stacks that are directly visible to and manipulated by the programmer.

The following is an example of manipulating a stack in Common Lisp (">" is the Lisp interpreter's prompt; lines not starting with ">" are the interpreter's responses to expressions): 

> (setf stack (list 'a 'b 'c))  ;; set the variable "stack"
(A B C)
> (pop stack)  ;; get top (leftmost) element, should modify the stack
A
> stack        ;; check the value of stack
(B C)
> (push 'new stack)  ;; push a new top onto the stack
(NEW B C)

Several of the C++ Standard Library container types have push_back and pop_back operations with LIFO semantics; additionally, the stack template class adapts existing containers to provide a restricted API with only push/pop operations. PHP has an SplStack class. Java's library contains a Stack class that is a specialization of Vector. Following is an example program in Java language, using that class. 

import java.util.Stack;

class StackDemo {
    public static void main(String[]args) {
        Stack<String> stack = new Stack<String>();
        stack.push("A");    // Insert "A" in the stack
        stack.push("B");    // Insert "B" in the stack
        stack.push("C");    // Insert "C" in the stack
        stack.push("D");    // Insert "D" in the stack
        System.out.println(stack.peek());    // Prints the top of the stack ("D")
        stack.pop();    // removing the top ("D")
        stack.pop();    // removing the next top ("C")
    }
}

Hardware stack

Main page: Stack-based memory allocation

A common use of stacks at the architecture level is as a means of allocating and accessing memory.

Basic architecture of a stack

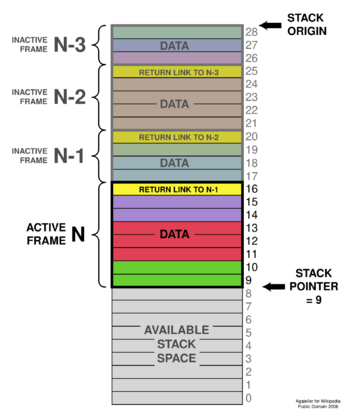
A typical stack is an area of computer memory with a fixed origin and a variable size. Initially the size of the stack is zero. A stack pointer, usually in the form of a processor register, points to the most recently referenced location on the stack; when the stack has a size of zero, the stack pointer points to the origin of the stack.

The two operations applicable to all stacks are:

  • A push operation: the address in the stack pointer is adjusted by the size of the data item and a data item is written at the location to which the stack pointer points.
  • A pop or pull operation: a data item at the current location to which the stack pointer points is read, and the stack pointer is moved by a distance corresponding to the size of that data item.

There are many variations on the basic principle of stack operations. Every stack has a fixed location in memory at which it begins. As data items are added to the stack, the stack pointer is displaced to indicate the current extent of the stack, which expands away from the origin.

Stack pointers may point to the origin of a stack or to a limited range of addresses above or below the origin (depending on the direction in which the stack grows); however, the stack pointer cannot cross the origin of the stack. In other words, if the origin of the stack is at address 1000 and the stack grows downwards (towards addresses 999, 998, and so on), the stack pointer must never be incremented beyond 1000 (to 1001 or beyond). If a pop operation on the stack causes the stack pointer to move past the origin of the stack, a stack underflow occurs. If a push operation causes the stack pointer to increment or decrement beyond the maximum extent of the stack, a stack overflow occurs.

Some environments that rely heavily on stacks may provide additional operations, for example:

  • Duplicate: the top item is popped and then pushed twice, such that two copies of the former top item now lie at the top.
  • Peek: the topmost item is inspected (or returned), but the stack pointer and stack size does not change (meaning the item remains on the stack). This can also be called the top operation.
  • Swap or exchange: the two topmost items on the stack exchange places.
  • Rotate (or Roll): the n topmost items are moved on the stack in a rotating fashion. For example, if n = 3, items 1, 2, and 3 on the stack are moved to positions 2, 3, and 1 on the stack, respectively. Many variants of this operation are possible, with the most common being called left rotate and right rotate.

Stacks are often visualized growing from the bottom up (like real-world stacks). They may also be visualized growing from left to right, where the top is on the far right, or even growing from top to bottom. The important feature is for the bottom of the stack to be in a fixed position. The illustration in this section is an example of a top-to-bottom growth visualization: the top (28) is the stack "bottom", since the stack "top" (9) is where items are pushed or popped from.

A right rotate will move the first element to the third position, the second to the first and the third to the second. Here are two equivalent visualizations of this process: 

apple                         banana
banana    ===right rotate==>  cucumber
cucumber                      apple

cucumber                      apple
banana    ===left rotate==>   cucumber
apple                         banana

A stack is usually represented in computers by a block of memory cells, with the "bottom" at a fixed location, and the stack pointer holding the address of the current "top" cell in the stack. The "top" and "bottom" nomenclature is used irrespective of whether the stack actually grows towards higher memory addresses.

Pushing an item on to the stack adjusts the stack pointer by the size of the item (either decrementing or incrementing, depending on the direction in which the stack grows in memory), pointing it to the next cell, and copies the new top item to the stack area. Depending again on the exact implementation, at the end of a push operation, the stack pointer may point to the next unused location in the stack, or it may point to the topmost item in the stack. If the stack points to the current topmost item, the stack pointer will be updated before a new item is pushed onto the stack; if it points to the next available location in the stack, it will be updated after the new item is pushed onto the stack.

Popping the stack is simply the inverse of pushing. The topmost item in the stack is removed and the stack pointer is updated, in the opposite order of that used in the push operation.

Stack in main memory

Many CISC-type CPU designs, including the x86, Z80 and 6502, have a dedicated register for use as the call stack stack pointer with dedicated call, return, push, and pop instructions that implicitly update the dedicated register, thus increasing code density. Some CISC processors, like the PDP-11 and the 68000, also have special addressing modes for implementation of stacks, typically with a semi-dedicated stack pointer as well (such as A7 in the 68000). In contrast, most RISC CPU designs do not have dedicated stack instructions and therefore most, if not all, registers may be used as stack pointers as needed.

Stack in registers or dedicated memory

Some machines use a stack for arithmetic and logical operations; operands are pushed onto the stack, and arithmetic and logical operations act on the top one or more items on the stack, popping them off the stack and pushing the result onto the stack. Machines that function in this fashion are called stack machines.

A number of mainframes and minicomputers were stack machines, the most famous being the Burroughs large systems. Other examples include the CISC HP 3000 machines and the CISC machines from Tandem Computers.

The x87 floating point architecture is an example of a set of registers organised as a stack where direct access to individual registers (relative to the current top) is also possible.

Having the top-of-stack as an implicit argument allows for a small machine code footprint with a good usage of bus bandwidth and code caches, but it also prevents some types of optimizations possible on processors permitting random access to the register file for all (two or three) operands. A stack structure also makes superscalar implementations with register renaming (for speculative execution) somewhat more complex to implement, although it is still feasible, as exemplified by modern x87 implementations.

Sun SPARC, AMD Am29000, and Intel i960 are all examples of architectures that use register windows within a register-stack as another strategy to avoid the use of slow main memory for function arguments and return values.

There is also a number of small microprocessors that implement a stack directly in hardware, and some microcontrollers have a fixed-depth stack that is not directly accessible. Examples are the PIC microcontrollers, the Computer Cowboys MuP21, the Harris RTX line, and the Novix NC4016. Many stack-based microprocessors were used to implement the programming language Forth at the microcode level.

Applications of stacks

Expression evaluation and syntax parsing

Calculators that employ reverse Polish notation use a stack structure to hold values. Expressions can be represented in prefix, postfix or infix notations and conversion from one form to another may be accomplished using a stack. Many compilers use a stack to parse syntax before translation into low-level code. Most programming languages are context-free languages, allowing them to be parsed with stack-based machines.

Backtracking

Another important application of stacks is backtracking. An illustration of this is the simple example of finding the correct path in a maze that contains a series of points, a starting point, several paths and a destination. If random paths must be chosen, then after following an incorrect path, there must be a method by which to return to the beginning of that path. This can be achieved through the use of stacks, as a last correct point can be pushed onto the stack, and popped from the stack in case of an incorrect path.

The prototypical example of a backtracking algorithm is depth-first search, which finds all vertices of a graph that can be reached from a specified starting vertex. Other applications of backtracking involve searching through spaces that represent potential solutions to an optimization problem. Branch and bound is a technique for performing such backtracking searches without exhaustively searching all of the potential solutions in such a space.

Compile-time memory management

A typical call stack, storing local data and call information for multiple levels of procedure calls. This stack grows downward from its origin. The stack pointer points to the current topmost datum on the stack. A push operation decrements the pointer and copies the data to the stack; a pop operation copies data from the stack and then increments the pointer. Each procedure called in the program stores procedure return information (in yellow) and local data (in other colors) by pushing them onto the stack. This type of stack implementation is extremely common, but it is vulnerable to buffer overflow attacks (see the text).

A number of programming languages are stack-oriented, meaning they define most basic operations (adding two numbers, printing a character) as taking their arguments from the stack, and placing any return values back on the stack. For example, PostScript has a return stack and an operand stack, and also has a graphics state stack and a dictionary stack. Many virtual machines are also stack-oriented, including the p-code machine and the Java Virtual Machine.

Almost all calling conventions‍—‌the ways in which subroutines receive their parameters and return results‍—‌use a special stack (the "call stack") to hold information about procedure/function calling and nesting in order to switch to the context of the called function and restore to the caller function when the calling finishes. The functions follow a runtime protocol between caller and callee to save arguments and return value on the stack. Stacks are an important way of supporting nested or recursive function calls. This type of stack is used implicitly by the compiler to support CALL and RETURN statements (or their equivalents) and is not manipulated directly by the programmer.

Some programming languages use the stack to store data that is local to a procedure. Space for local data items is allocated from the stack when the procedure is entered, and is deallocated when the procedure exits. The C programming language is typically implemented in this way. Using the same stack for both data and procedure calls has important security implications (see below) of which a programmer must be aware in order to avoid introducing serious security bugs into a program.

Efficient algorithms

Several algorithms use a stack (separate from the usual function call stack of most programming languages) as the principal data structure with which they organize their information. These include:

  • Graham scan, an algorithm for the convex hull of a two-dimensional system of points. A convex hull of a subset of the input is maintained in a stack, which is used to find and remove concavities in the boundary when a new point is added to the hull.[19]
  • Part of the SMAWK algorithm for finding the row minima of a monotone matrix uses stacks in a similar way to Graham scan.[20]
  • All nearest smaller values, the problem of finding, for each number in an array, the closest preceding number that is smaller than it. One algorithm for this problem uses a stack to maintain a collection of candidates for the nearest smaller value. For each position in the array, the stack is popped until a smaller value is found on its top, and then the value in the new position is pushed onto the stack.[21]
  • The nearest-neighbor chain algorithm, a method for agglomerative hierarchical clustering based on maintaining a stack of clusters, each of which is the nearest neighbor of its predecessor on the stack. When this method finds a pair of clusters that are mutual nearest neighbors, they are popped and merged.[22]

Security

Some computing environments use stacks in ways that may make them vulnerable to security breaches and attacks. Programmers working in such environments must take special care to avoid such pitfalls in these implementations.

As an example, some programming languages use a common stack to store both data local to a called procedure and the linking information that allows the procedure to return to its caller. This means that the program moves data into and out of the same stack that contains critical return addresses for the procedure calls. If data is moved to the wrong location on the stack, or an oversized data item is moved to a stack location that is not large enough to contain it, return information for procedure calls may be corrupted, causing the program to fail.

Malicious parties may attempt a stack smashing attack that takes advantage of this type of implementation by providing oversized data input to a program that does not check the length of input. Such a program may copy the data in its entirety to a location on the stack, and in doing so, it may change the return addresses for procedures that have called it. An attacker can experiment to find a specific type of data that can be provided to such a program such that the return address of the current procedure is reset to point to an area within the stack itself (and within the data provided by the attacker), which in turn contains instructions that carry out unauthorized operations.

This type of attack is a variation on the buffer overflow attack and is an extremely frequent source of security breaches in software, mainly because some of the most popular compilers use a shared stack for both data and procedure calls, and do not verify the length of data items. Frequently, programmers do not write code to verify the size of data items, either, and when an oversized or undersized data item is copied to the stack, a security breach may occur.

See also


Notes

  1. ↑ By contrast, a queue operates first in, first out, referred to by the acronym FIFO.

References

  1. ↑ 1.0 1.1 Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. pp. 232–233. ISBN 0-262-03384-4. 
  2. ↑ Proposals for Development in the Mathematics Division of an Automatic Computing Engine (ACE). 1946-03-19.  (NB. Presented on 1946-03-19 before the Executive Committee of the National Physical Laboratory (Great Britain).)
  3. ↑ "The other Turing machine". The Computer Journal 20 (3): 269–279. 1977-01-01. doi:10.1093/comjnl/20.3.269.  (11 pages)
  4. ↑ Computer architecture: Concepts and evolution. Boston, Massachusetts, USA: Addison-Wesley Longman Publishing Co., Inc.. 1997. 
  5. ↑ "2.1 Lukasiewicz and the First Generation: 2.1.2 Germany: Konrad Zuse (1910–1995); 2.2 The First Generation of Stack Computers: 2.2.1 Zuse Z4". Second-Generation Stack Computer Architecture (thesis). Waterloo, Canada: University of Waterloo. April 2007. pp. 8, 11. http://fpgacpu.ca/publications/Second-Generation_Stack_Computer_Architecture.pdf. Retrieved 2022-07-02.  (178 pages)
  6. ↑ (in de) Probleme der Programmierungstechnik. Berlin, Germany: VEB Deutscher Verlag der Wissenschaften. 1957. pp. 61–68.  (NB. This paper was first presented in 1955. It describes a number stack (Zahlenkeller), but names it linear auxiliary memory (linearer Hilfsspeicher).)
  7. ↑ 7.0 7.1 7.2 7.3 (in de) Keller, Stack und automatisches Gedächtnis – eine Struktur mit Potenzial (Tagungsband zum Kolloquium 14. November 2014 in Jena). GI Series: Lecture Notes in Informatics (LNI) – Thematics. T-7. Bonn, Germany: Gesellschaft für Informatik (GI) / Köllen Druck + Verlag GmbH. 2015. ISBN 978-3-88579-426-4. https://dl.gi.de/bitstream/handle/20.500.12116/4381/lni-t-7.pdf?sequence=1&isAllowed=y. Retrieved 2020-04-12.  [1] (77 pages)
  8. ↑ "Verfahren zur automatischen Verarbeitung von kodierten Daten und Rechenmaschine zur Ausübung des Verfahrens" (in de). Munich, Germany: Deutsches Patentamt. 1957-03-30. https://worldwide.espacenet.com/publicationDetails/originalDocument?CC=DE&NR=1094019&KC=&FT=E. 
  9. ↑ (in de) Informatik – Eine einführende Übersicht. Part 1 (3 ed.). Berlin: Springer-Verlag. 1982. p. 222. ISBN 3-540-11722-9. "Die Bezeichnung 'Keller' hierfür wurde von Bauer und Samelson in einer deutschen Patentanmeldung vom 30. März 1957 eingeführt." 
  10. ↑ "Sequentielle Formelübersetzung" (in de). Elektronische Rechenanlagen 1 (4): 176–182. 1959. 
  11. ↑ "Sequential Formula Translation". Communications of the ACM 3 (2): 76–83. 1960. doi:10.1145/366959.366968. 
  12. ↑ "IEEE-Computer-Pioneer-Preis – Bauer, Friedrich L.". Technical University of Munich, Faculty of Computer Science. 1989-01-01. https://www.in.tum.de/forschung/auszeichnungen/detail/newsarticle/ieee-computer-pioneer-preis.html. 
  13. ↑ An Addressless Coding Scheme based on Mathematical Notation (typescript). N.S.W. University of Technology. May 1957. pp. 121-1 – 121-12. https://www.massey.ac.nz/~rmclachl/DPACM/121%20-%20addressless%20coding%20scheme.pdf. Retrieved 2020-04-12.  (12 pages)
  14. ↑ (in de) Ziffern-Rechenautomat mit Programmierung nach mathematischem Formelbild (Habilitation thesis). Jena, Germany: Mathematisch-naturwissenschaftliche Fakultät, Friedrich-Schiller-Universität. 1958-12-11. urn:nbn:de:gbv:27-20130731-133019-7. PPN:756275237. http://www.db-thueringen.de/servlets/DocumentServlet?id=22616. Retrieved 2023-10-14.  [2] (2+69 pages)
  15. ↑ (in de) Ziffernrechenautomaten. Elektronisches Rechnen und Regeln. 1. Berlin, Germany: Akademie-Verlag. 1960. 
  16. ↑ Algorithms for RPN calculators (1 ed.). Cambridge, Massachusetts, USA: Wiley-Interscience, John Wiley & Sons, Inc.. 1978. ISBN 978-0-471-03070-6. https://archive.org/details/algorithmsforrpn0000ball. 
  17. ↑ Computer Architecture. Technical Publications. 2010-01-01. pp. 1–56. ISBN 978-8-18431534-9. https://books.google.com/books?id=mOaXS_x-iW4C&pg=PR1. Retrieved 2015-01-30. 
  18. ↑ Fundamentals of Data Structures in Pascal. Computer Science Press. 1984. p. 67. 
  19. ↑ An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set. Information Processing Letters 1. 1. 1972. pp. 132–133. http://www.math.ucsd.edu/~ronspubs/72_10_convex_hull.pdf. 
  20. ↑ "Geometric applications of a matrix-searching algorithm". Algorithmica 2 (1–4): 195–208. 1987. doi:10.1007/BF01840359. .
  21. ↑ "Optimal doubly logarithmic parallel algorithms based on finding all nearest smaller values". Journal of Algorithms 14 (3): 344–370. 1993. doi:10.1006/jagm.1993.1018. .
  22. ↑ "A survey of recent advances in hierarchical clustering algorithms". The Computer Journal 26 (4): 354–359. 1983. doi:10.1093/comjnl/26.4.354. http://www.multiresolutions.com/strule/old-articles/Survey_of_hierarchical_clustering_algorithms.pdf. .

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Stack_(abstract_data_type)&oldid=3358047"