Book (graph theory)

A triangular book

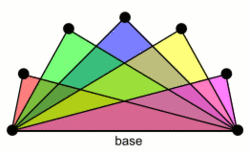
In graph theory, a book graph (often written [math]\displaystyle{ B_p }[/math] ) may be any of several kinds of graph formed by multiple cycles sharing an edge.

Variations

One kind, which may be called a quadrilateral book, consists of p quadrilaterals sharing a common edge (known as the "spine" or "base" of the book). That is, it is a Cartesian product of a star and a single edge. The 7-page book graph of this type provides an example of a graph with no harmonious labeling.

A second type, which might be called a triangular book, is the complete tripartite graph K_1,1,p. It is a graph consisting of [math]\displaystyle{ p }[/math] triangles sharing a common edge. A book of this type is a split graph. This graph has also been called a [math]\displaystyle{ K_e(2,p) }[/math] or a thagomizer graph (after thagomizers, the spiked tails of stegosaurian dinosaurs, because of their pointy appearance in certain drawings) and their graphic matroids have been called thagomizer matroids. Triangular books form one of the key building blocks of line perfect graphs.

The term "book-graph" has been employed for other uses. Barioli used it to mean a graph composed of a number of arbitrary subgraphs having two vertices in common. (Barioli did not write [math]\displaystyle{ B_p }[/math] for his book-graph.)

Within larger graphs

Given a graph [math]\displaystyle{ G }[/math], one may write [math]\displaystyle{ bk(G) }[/math] for the largest book (of the kind being considered) contained within [math]\displaystyle{ G }[/math].

Theorems on books

Denote the Ramsey number of two triangular books by [math]\displaystyle{ r(B_p,\ B_q). }[/math] This is the smallest number [math]\displaystyle{ r }[/math] such that for every [math]\displaystyle{ r }[/math]-vertex graph, either the graph itself contains [math]\displaystyle{ B_p }[/math] as a subgraph, or its complement graph contains [math]\displaystyle{ B_q }[/math] as a subgraph.

• If [math]\displaystyle{ 1\leq p\leq q }[/math], then [math]\displaystyle{ r(B_p,\ B_q)=2q+3 }[/math].
• There exists a constant [math]\displaystyle{ c=o(1) }[/math] such that [math]\displaystyle{ r(B_p,\ B_q)=2q+3 }[/math] whenever [math]\displaystyle{ q\geq cp }[/math].
• If [math]\displaystyle{ p\leq q/6+o(q) }[/math], and [math]\displaystyle{ q }[/math] is large, the Ramsey number is given by [math]\displaystyle{ 2q+3 }[/math].
• Let [math]\displaystyle{ C }[/math] be a constant, and [math]\displaystyle{ k = Cn }[/math]. Then every graph on [math]\displaystyle{ n }[/math] vertices and [math]\displaystyle{ m }[/math] edges contains a (triangular) [math]\displaystyle{ B_k }[/math].