Boxcar function

A graphical representation of a boxcar function

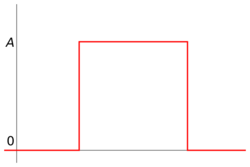
In mathematics, a boxcar function is any function which is zero over the entire real line except for a single interval where it is equal to a constant, A. The function is named after its graph's resemblance to a boxcar, a type of railroad car. The boxcar function can be expressed in terms of the uniform distribution as [math]\displaystyle{ \operatorname{boxcar}(x)= (b-a)A\,f(a,b;x) = A(H(x-a) - H(x-b)), }[/math] where f(a,b;x) is the uniform distribution of x for the interval [a, b] and [math]\displaystyle{ H(x) }[/math] is the Heaviside step function. As with most such discontinuous functions, there is a question of the value at the transition points. These values are probably best chosen for each individual application.

When a boxcar function is selected as the impulse response of a filter, the result is a simple moving average filter, whose frequency response is a sinc-in-frequency, a type of low-pass filter.

See also

• Boxcar averager
• Rectangular function
• Step function
• Top-hat filter