Brianchon's theorem
In geometry, Brianchon's theorem is a theorem stating that when a hexagon is circumscribed around a conic section, its principal diagonals (those connecting opposite vertices) meet in a single point. It is named after Charles Julien Brianchon (1783–1864).
Formal statement
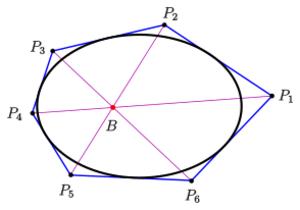
Let [math]\displaystyle{ P_1P_2P_3P_4P_5P_6 }[/math] be a hexagon formed by six tangent lines of a conic section. Then lines [math]\displaystyle{ \overline{P_1P_4},\; \overline{P_2P_5},\; \overline{P_3P_6} }[/math] (extended diagonals each connecting opposite vertices) intersect at a single point [math]\displaystyle{ B }[/math], the Brianchon point.[1]:p. 218[2]
Connection to Pascal's theorem
The polar reciprocal and projective dual of this theorem give Pascal's theorem.
Degenerations
As for Pascal's theorem there exist degenerations for Brianchon's theorem, too: Let coincide two neighbored tangents. Their point of intersection becomes a point of the conic. In the diagram three pairs of neighbored tangents coincide. This procedure results in a statement on inellipses of triangles. From a projective point of view the two triangles [math]\displaystyle{ P_1P_3P_5 }[/math] and [math]\displaystyle{ P_2P_4P_6 }[/math] lie perspectively with center [math]\displaystyle{ B }[/math]. That means there exists a central collineation, which maps the one onto the other triangle. But only in special cases this collineation is an affine scaling. For example for a Steiner inellipse, where the Brianchon point is the centroid.
In the affine plane
Brianchon's theorem is true in both the affine plane and the real projective plane. However, its statement in the affine plane is in a sense less informative and more complicated than that in the projective plane. Consider, for example, five tangent lines to a parabola. These may be considered sides of a hexagon whose sixth side is the line at infinity, but there is no line at infinity in the affine plane. In two instances, a line from a (non-existent) vertex to the opposite vertex would be a line parallel to one of the five tangent lines. Brianchon's theorem stated only for the affine plane would therefore have to be stated differently in such a situation.
The projective dual of Brianchon's theorem has exceptions in the affine plane but not in the projective plane.
Proof
Brianchon's theorem can be proved by the idea of radical axis or reciprocation. To prove it take an arbitrary length (MN) and carry it on the tangents starting from the contact points: PL = RJ = QH = MN etc. Draw circles a, b, c tangent to opposite sides of the hexagon at the created points (H,W), (J,V) and (L,Y) respectively. One sees easily that the concurring lines coincide with the radical axes ab, bc, ca resepectively, of the three circles taken in pairs. Thus O coincides with the radical center of these three circles.
The theorem takes particular forms in the case of circumscriptible pentagons e.g. when R and Q tend to coincide with F, a case where AFE is transformed to the tangent at F. Then, taking a further similar identification of points T,C and U, we obtain a corresponding theorem for quadrangles.
See also
References
- ↑ Whitworth, William Allen. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions, Forgotten Books, 2012 (orig. Deighton, Bell, and Co., 1866). http://www.forgottenbooks.com/search?q=Trilinear+coordinates&t=books
- ↑ Coxeter, H. S. M. (1987). Projective Geometry (2nd ed.). Springer-Verlag. pp. Theorem 9.15, p. 83. ISBN 0-387-96532-7.
 |